АЛГОРИТМ — что это. Понятие, свойства, структура и виды
Алгоритм. Практически все в нашем мире подчиняется каким-то законам и правилам. Современная наука не стоит на месте, благодаря чему человечеству известна масса формул и алгоритмов, следуя которым, можно рассчитать и воссоздать множество действий и строений, созданных природой, и воплотить в жизнь идеи, придуманные человеком. В этой статье мы разберем основные понятия алгоритма.
История появления алгоритмов
Алгоритм — понятие, появившиеся в XII веке. Само слово «алгоритм» происходит от латинской интерпретации имени известного математика среднего востока Мухаммеда аль Хорезми, который написал книгу «Об индийском счете». В этой книге описано, как правильно записывать натуральные числа, используя арабские цифры, и приведено описание алгоритма действий столбиком над такими числами.
В XII веке книга «Об индийском счете» была переведена на латинский язык, тогда-то и появилось данное определение.
Взаимодействие алгоритма с человеком и машиной
Создание алгоритма требует творческого подхода, поэтому новый список последовательных действий может создать только живое существо. А вот для исполнения уже существующих инструкций фантазию иметь не обязательно, с этим справится даже бездушная техника.
Отличным примером точного исполнения заданной инструкции является пустая микроволновая печь, которая продолжает работать, несмотря на отсутствие пищи внутри нее.
Субъект или объект, которому не обязательно вникать в суть алгоритма, называется формальным исполнителем. Человек тоже может стать формальным исполнителем, однако в случае нерентабельности того или иного действия мыслящий исполнитель может все сделать по-своему. Поэтому основными исполнителями являются компьютеры, микроволновые печи, телефоны и другая техника. Понятие алгоритма в информатике имеет самое важное значение. Каждый алгоритм составляется с расчетом на конкретного субъекта, с учетом допустимых действий. Те объекты к которым субъект может применить инструкции, составляют среду исполнителя.
Практически все в нашем мире подчиняется каким-то законам и правилам. Современная наука не стоит на месте, благодаря чему человечеству известна масса формул и алгоритмов, следуя которым, можно рассчитать и воссоздать множество действий и творений природы и воплотить в жизнь идеи, придуманные человеком. В этой статье мы разберем основные понятия алгоритма.
Что такое алгоритм?
Большинство действий, которые мы выполняем в течение своей жизни, требуют соблюдений ряда правил. От того, насколько верное представление имеет человек о том что, как и в какой последовательности он должен сделать, зависит качество и результат выполнения поставленных перед ним задач. С детства родители пытаются выработать в своем чаде алгоритм основных действий, например: проснуться, заправить постель, умыться и почистить зубы, сделать зарядку, позавтракать и т. д., список, который человек всю жизнь выполняет с утра тоже можно считать своеобразным алгоритмом.
Алгоритм — это понятие, обозначающее подборку инструкций, которые необходимо выполнять человеку для того, чтобы решить определенную задачу.
Вообще, алгоритм имеет множество определений, несколько ученых характеризуют его по-разному.
Если алгоритм, применяемый человеком ежедневно, у каждого свой, и может изменятся в зависимости от возраста и ситуаций, в которых оказывается исполнитель, то свод действий, которые нужно выполнить для решения математической задачи или для использования техники, един для всех и всегда остается неизменным.
Существует разное понятие алгоритма, виды алгоритмов тоже разнятся — к примеру, для человека, который преследует какую-либо цель, и для техники.
В наш век информационных технологий люди ежедневно выполняют свод инструкций, созданных до них другими людьми, ведь техника требует при использовании точного исполнения ряда действий. Поэтому основная задача преподавателей в школах — научить детей пользоваться алгоритмами, быстро схватывать и изменять уже существующие правила в соответствии со сложившейся ситуацией. Структура алгоритма является одним из тех понятий, которое изучается на уроке математики и информатики в каждой школе.
Основные свойства алгоритма
Часто в школах, чтобы дать детям более понятное описание алгоритмов, учителя приводят в пример приготовление пищи по кулинарной книге, изготовление лекарства по рецепту или процесс мыловарения на основе мастер-класса. Однако, учитывая второе свойство алгоритма, в котором говорится о том, что каждый пункт алгоритма должен быть настолько понятным, чтобы его мог выполнить абсолютно любой человек и даже машина, можно прийти к выводу что любой процесс, требующий проявления хоть какой-то фантазии, алгоритмом назвать нельзя. А готовка и рукоделие требуют определенных навыков и хорошо развитого воображения.
Существуют разные типы алгоритмов, но есть три основных.
Цикличный алгоритм
В таком типе некоторые пункты повторяются по несколько раз. Список действий, которые необходимо повторить для достижения цели, называется телом алгоритма.
Итерация цикла — это выполнение всех пунктов, входящих в тело цикла. Части цикла, которые постоянно выполняются определенное количество раз, называются циклом с фиксированным числом итераций.
Те части цикла, частота повторения которых зависит от ряда условий, называются неопределёнными.
Самый простой вид цикла — это фиксированный.
Линейные типы алгоритмов
Инструкции таких схем выполняются однократно в той последовательности, в которой они представлены. Например, линейным алгоритмом можно считать процесс заправки постели или чистки зубов. Также к этому типу относятся математические примеры, где присутствуют лишь действия сложения и вычитания.
Разветвляющийся алгоритм
В разветвляющимся типе есть несколько вариантов действий, какое из них будет применено, зависит от условия.
Пример. Вопрос: «Идет дождь?» Варианты ответов: «Да» или «Нет». Если «да» — откройте зонт, если «нет» — положите зонт в сумку.
Вспомогательный алгоритм
Вспомогательный алгоритм можно использовать в других алгоритмах, указав лишь его название.
Термины, встречающиеся в алгоритмах
Условие находится между словами «если» и «тогда».
Например: если вы знаете английский язык, тогда нажмите один. В этом предложении условием будет часть фразы «вы знаете английский язык».
Данные — сведения, которые несут определенную смысловую нагрузку и представлены в таком виде, чтобы их можно было передавать и использовать для данного алгоритма.
Алгоритмический процесс — решение задачи по алгоритму с применением определенных данных.
Структура алгоритма
Алгоритм может иметь различную структуру. Для того чтобы описать алгоритм, понятие которого зависит и от его строения, можно воспользоваться целым рядом различных способов, например: словесный, графический, с помощью специально разработанного алгоритмического языка.
Какой из способов будет использован, зависит от нескольких факторов: от сложности задачи, от того, насколько нужно детализировать процесс решения задачи и т. д.
Графический вариант построения алгоритма
Графический алгоритм — понятие, подразумевающие под собой разложение действий, которые нужно выполнить для решения определенной задачи, по определенным геометрическим фигурам.
Графические схемы изображаются не как попало. Для того чтобы их мог понять любой человек применяются чаще всего блок-схемы и структурограммы Насси-Шнейдермана.
Также блок-схемы изображаются в соответствии с ГОСТ-19701-90 и ГОСТ-19.003-80.
Графические фигуры, применяемые в алгоритме, делятся на:
В графическом алгоритме геометрические фигуры, используемые для обозначения данных, называются блоками.
Все блоки идут в последовательности «сверху вниз» и «слева направо» — это правильное направление потока. При правильной последовательности линии, соединяющие между собой блоки, не показывают направление. В остальных случаях направление линий обозначается с помощью стрелок.
У правильной схемы алгоритма не должно быть больше одного выхода из обрабатывающих блоков и менее двух выходов из блоков, отвечающих за логические операции и проверку выполнения условий.
Как правильно построить алгоритм?
Структура алгоритма, как было сказано выше, должна строиться по ГОСТ, иначе она не будет понятна и доступна окружающим.
Общая методика по записи включает в себя следующие пункты:
При составлении алгоритма следует отметить действия, которые позволят производить нужные для решения задачи действия над выбранными данными. Примерный вид алгоритма:
Правильное построение схемы существенно облегчит вычисление алгоритмов.
Геометрические фигуры, отвечающие за разные действия в алгоритме
Горизонтально расположенный овал — начало и конец (знак завершения).
Горизонтально расположенный прямоугольник — вычисление или другие действия (знак процесса).
Горизонтально расположенный параллелограмм — ввод или вывод (знак данных).
Горизонтально расположенный ромб — проверка условия (знак решения).
Вытянутый, горизонтально расположенный шестиугольник — модификация (знак подготовки).
Модели алгоритмов представлены ниже на рисунке.
Формульно-словестный вариант построения алгоритма.
Формульно-словестные алгоритмы записываются в произвольной форме, на профессиональном языке той области, к которой относится задача. Описание действий таким способом осуществляют с помощью слов и формул.
Понятие алгоритма в информатике
В компьютерной сфере все строится на алгоритмах. Без четких указаний, введенных в виде специального кода, не будет работать ни одна техника или программа. На уроках информатики ученикам стараются дать основные понятия алгоритмов, научить пользоваться ими и самостоятельно их создавать.
Создание и использование алгоритмов в информатике — процесс более творческий, чем, например, выполнение указаний к решению задачи в математике.
Существует также специальная программа «Алгоритм», которая помогает людям, несведущим в области программирования, создавать свои собственные программы. Такой ресурс сможет стать незаменимым помощником для тех, кто делает первые шаги в информатике и хочет создавать свои игры или любые другие программы.
С другой стороны, любая программа — алгоритм. Но если алгоритм несет в себе лишь действия, которые нужно выполнять, вставляя свои данные, то программа уже несет в себе готовые данные. Еще одно отличие — это то, что программа может быть запатентована и являться частной собственностью, а алгоритм нет. Алгоритм — понятие более обширное, нежели программа.
Вывод
В этой статье мы разобрали понятие алгоритма и его виды, узнали, как правильно записывать графические схемы.
Что такое алгоритм?! Часть первая
Терзаем вместе основной кирпичик программиста — Алгоритм.
Проблема
Текущее состояние в области программирования — это обучение ремеслу по большей части личной практикой или разборами примеров стороннего кода, с которым по каким-то причинам приходится сталкиваться.
В результате программированию учишься по наитию. Лишь немного в этом труде помогают сборники алгоритмов, прикладных техник и шаблонов проектирования. Общая совокупность предлагаемых ими рецептов выстраивается длинным списком, и его длина грозит каждому из прочитанных приемов быть позабытым (как была забыта 53-яя личная группа в «телеге» до введения разбиения по каталогам). Но даже тот прием, который остался в памяти, чаще всего просто является описанием прикладной задачи, в которой было успешно его использование.
Почему конкретный прием был успешен в задаче-образце? Будет ли он успешен в твоём проекте? Какие признаки проекта дают понять, что использование приёма уместно?
В личном опыте существования в профессии не раз отмечено, что каждый Junior борется с одинаковыми ветряными мельницами и постигает методы создания программ основываясь только на своих ошибках. Но ведь такие ошибки совершили уже очень многие. Почему до сих пор не создана система правил программирования, которая поможет обойти новоиспеченному кораблю-программисту подводные прибрежные камни? Ну, например, объяснение вреда использования метода «Copy-Paste» для развития кода. Если такие правила получится объяснить малым набором причин, их сформировавшим, то это объяснение обеспечит их запоминание и последующее использование в практике, тем самым поможет уклониться от бесчисленных грабель, разложенных тут и там.
Для компактного и полезного набора объяснений нужно:
Если обобщить, то нужны алгоритмы для написания и развития алгоритмов.
Задуманная серия статей не претендует на полное решение указанной проблемы. Предпринимается небесспорная попытка сделать первый шаг на пути к этому решению. Этот шаг состоит в выделении структуры и свойств главного кирпичика программиста — Алгоритма.
Задача
Сформулируем основную задачу, которую хочется решить. Для этого сначала запишем операции над алгоритмами, которые программист выполняет в ходе написания своего проекта:
Рассмотрим существующие на текущий момент варианты значения слова «алгоритм» в поисках подсказок, о том как можно работать с алгоритмами.
Так, например, формулировка «конечная совокупность точно заданных правил решения произвольного класса задач» говорит что есть возможность как-то «точно задать правила» из них собрать «совокупность» и этой совокупностью «решить» некоторый «класс задач».
Сразу возникает масса вопросов к этому определению:
Другая формулировка «набор инструкций, описывающих порядок действий исполнителя для решения некоторой задачи» говорит что есть «исполнитель», который может выполнять некоторые «действия», и при некотором «порядке» выполнения этих «действий» «решается задача». Вопросов не стало меньше:
Перечислено много вопросов, но они мало помогают в поиске методов работы с алгоритмом. Поэтому поставим себе меньшую задачу, но тоже очень нам важную. Давайте попробуем сформулировать, что делает алгоритм способом решения наших задач, и какие процессы являются для него «действиями». Даже решение этой «маленькой» задачи оказывается очень объемным для одной статьи, поэтому будем его разбивать на части. И поэтому первую статью серии целиком посвятим только «Действию» и его признакам, которые опущены в указанных выше определениях алгоритма, но являются очень важными для ответов на все заданные вопросы.
Определение алгоритма
Рассмотрим определение алгоритма, говорящее, что он — приводящая к решению задачи последовательность действий. Как программисту мне приходится писать много кода. Этот код состоит из частей. Такими частями являются и функции, и классы, и модули. Когда я пишу текст функции — я занимаюсь написанием алгоритма.
Раньше алгоритм создавали в виде блок схем и полуавтоматически компилировали в машинные коды. Сейчас я избавлен от необходимости быть художником и компилятором для написания программы. Текст моей функции — это запись алгоритма в текстовом виде — его текстовая блок-схема. Здесь можно вспомнить Scratch, где используется визуальное создание блок-схемы алгоритма без написания текста. Способ записи алгоритма сейчас не так важен.
Важно, что в написании алгоритма функции я могу использовать вызовы других функции, которые я или другой программист уже написал до этого момента. Вспоминая фразу «последовательность действий, приводящая к решению задачи», можно отметить, что функции, написанные ранее, являются моими «действиями». То есть «действия» могут быть функциями. Если обобщать, то «действия» могут быть алгоритмами.
Если «действие = алгоритм», то определение можно попробовать переписать рекурсивно «алгоритм — это приводящая к решению задачи последовательность использования существующих алгоритмов». Рекурсивные определение не самое простое, что можно записать в словаре обычного человека. Но для программиста и математика эта форма знакома. Мы умеем с ней работать, и это даёт нам преимущество в рассмотрении разных задач, разбиваемых на подобные себе подзадачи. Так давайте воспользуемся этим преимуществом.
Чтобы разрешить рекурсию нам необходимо найти:
Действие
Для начала рассмотрим «действие» и попробуем найти причину, обеспечивающую возможность использования существующего «действия» для создания нового алгоритма.
Этой причиной является возможность повторного использования «действия» с получением тождественного результата. Только тогда разработанный с использованием этого «действия» алгоритм решения некоторой задачи будет одинаково решать эту задачу снова и снова. Мы нащупали важные законы нашего мира, в котором:
Какие признаки «действия» кроме повторимости делают возможным его использование в создании алгоритма? Что является терминальным неделимым «действием»? Чтобы ответить на этот вопрос стоит рассмотреть разные примеры «действий» из нашего опыта. Программисты встречали их много раз. Это и сложение, и умножение, и установка цвета пикселя на экране. Но мы знакомы с ними и вне программирования. Вся наука основывается на повторяемых явлениях.
Закон гравитации, описывающий повторяющееся явление падения яблока, тоже может стать действием. Ведь любое яблоко будет падать на землю? Значит этот процесс можно использовать в качестве «действия»! Например решая задачу прогнать Ньютона от яблони, на которую Вы случайно забрались ранее.
Рассмотрим, что происходит при выполнении «действия». Например, во время падения яблока с ветки яблони на землю. В этом процессе происходит несколько изменений. Если вспомнить школьную физику и рассмотреть ситуацию в системе отсчета, привязанной к Земле, то сила гравитации вызывает изменение скорости яблока, разгоняя его. При этом в процессе отмечается еще одно важное изменение — уменьшается расстояние между яблоком и Землей.
В рамках примера процесса «Земля-Яблоко» можно отметить у «действия» следующие признаки:
Рассмотрим с этими признаками разные области и процессы, выделяя в них примеры «действий» и контролируя особенности указанных признаков в описании структуры «действия».
Физические процессы
Для физических систем, процессы которых мы наблюдаем в нашем мире, характерные объекты и изменения опираются на фундаментальные взаимодействия и потому их достаточно просто выделить по аналогии с гравитационным взаимодействием Земли и яблока. Например, для системы из протона и электрона или системы двух протонов.
Отдельно от этих простых взаимодействий двух объектов стоят многокомпонентные процессы, например, ядерные реакции (по структуре «действия» близки к химическим процессам, рассматриваемым далее). Сложны и процессы описываемые суммарным взаимодействием большого числа элементов, например, «идеальный газ». Пока отложим их рассмотрение и сосредоточимся на самых простых примерах.
Химические процессы
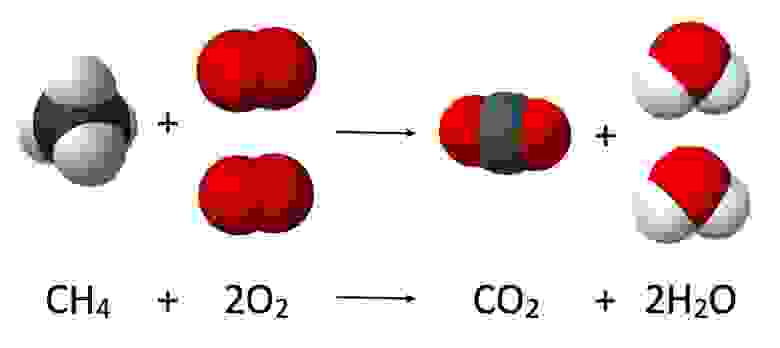
Перейдем к следующей большой области — химическим процессам. Химические реакции (например, 
) по признаку своей повторимости так же являются «действиями». Объектами в них являются атомы и молекулы. Для описания происходящих изменений необходимо немного преобразовать «физические» изменения. Так изменения параметров движения в совокупности дают нам изменение температуры в ходе химической реакции. А среди изменений расстояний между молекулами мы, игнорируя броуновское движение, можем выделить фиксацию расстояния в виде повторимого формирования и разрушения связей между частями взаимодействующих молекул. Локальность для химической реакции тоже существует — это отсутствие реакции при нахождении гидроксида натрия и соляной кислоты в разных пробирках и наличие реакции при соприкосновении веществ. Конечно, в «химической» области «действий» есть особенности не сводящиеся к молекулам, например, фотохимические реакции, где к объектам необходимо добавить фотоны. Самые простые процессы выбраны для рассмотрения намеренно.
Математические процессы
Следующей областью выберем «действия» из известных нам абстрактных алгоритмов. Самые яркие их представители — математические процессы. В этой области есть действительно «сложные случаи», но для этой статьи достаточно хорошо знакомых примеров. Рассмотрим в качестве «действия» достаточно элементарную операцию — сложение. А примером этого «действия» выберем сложение математиком двух целых чисел.
В ситуации с математиком можно выделить много объектов, но с точки зрения «действия» («сложение математиком двух целых чисел»), объекта всего три: это объект «математик», объект «первое число» и объект «второе число». В отличие от всех рассмотренных ранее объектов числа являются обозначениями, то есть виртуальными объектами. И их преобразование в алгоритме более сложно устроено нежели изменение расстояния и параметров движения объектов, как это было для «химических» действий. Подробности такого преобразования — это тема отдельной увлекательной статьи. А в рамках текущей рассмотрим древнего математика, который складывает числа, используя кучки камешков (рим. ‘calculi’), и более «современного» математика, использующего абак. Абстракции таких способов вычисления суммы не так далеко отошли от физических и химических процессов, поэтому структура процессов их «действий» полностью описывается изменениями расстояний и связей.
Интересно, что на примере древнего математика становится понятен смысл слова «сложить», которое отсылает нас к действию «класть» и к фразе «положить вместе».
Сложение и древний математик
Для математика, оперирующего камешками, сумма это «действие» со следующими характеристиками.
Сложение и математик-абакист
У математика с абаком ситуация сложнее. Кучки разделены по значению на разрядные борозды.
Можно рассмотреть самый простой абак с двумя разрядами-бороздами. Пусть он будет десятичный. Тогда один камешек на борозде десятков соответствует десяти камешкам на борозде единиц. И 10 — это максимальное количество камешков на борозде единиц. По сравнению с действием первого математика меняется представление слагаемых. И в арсенале математика уже необходимы нескольких готовых «действий».
Локальность в этих математических «действиях» описывается отсутствием взаимодействия двух слагаемых, находящихся далеко от математика, и запуском процессов сложения когда все три объекта сложения «близко». Повторяемое изменение в математическом «действии» выражается в изменении связей между камнями и удерживающими их локациями (кучками, бороздами).
Сложение и машина Тьюринга
Можно пойти чуть дальше и заменить математика в таких «действиях» на «управляющее устройство» машины Тьюринга. Тогда «ячейки ленты» машины Тьюринга будут содержать слагаемые.
При этом остаётся и признак локальности как возможность взаимодействия управляющего устройства только с текущей ячейкой ленты, и признак изменения параметров объектов, который можно описать как изменение состояния ячеек.
Подробное описание исходных и результирующих состояний объектов, а так же «действий» производящих эти изменения для сложения, исполняемого машиной Тьюринга, оставим за рамками этой статьи. Но упомянем, что перейдя к машине мы снижаем требования к исполнителю «действия», что является главным способом для создания формальных методов работы с алгоритмом. Можно поставить себе целью упрощение каждой составляющей алгоритма до состояния, когда её выполнение можно будет поручить компьютеру. Тогда в определении алгоритма не останется тёмных мест, и многочисленные вопросы, перечисленные в начале, найдут свои ответы. Пока формализован только исполнитель. Скажем спасибо за это Тьюрингу и вспомним про «действие», формализация которого уже на пороге.
Выводы
Соберём всё, что мы отметили рассматривая разные примеры «действия»:
Признак Повторимости помогает нам в создании наших алгоритмов. С его использованием мы из всех процессов выделяем те, что являются «действием» и на их основе создаём новые алгоритмы. Более того этот признак достаточно прост и на основе его формализации можно снизить требования к системе обнаруживающей и создающей «действия» и поручить это нашему компьютеру.
Следующая статья серии (Часть 2) будет посвящена рассмотрению способов, с использованием которых «действия» могут быть сгруппированы в алгоритм. Этих способов достаточно много и есть предпосылки, что их описание не получится уместить в одну статью. Напишем — увидим.
Спасибо Вам за внимание.
Отзывы
Буду очень благодарен за отзывы и предложения, так как они помогают мне скорректировать направление развития работы в области.
Отдельное волнение у меня есть по стилю и форматированию, используемым в статье (кавычки, абзацы, курсив). Напишите, пожалуйста, если у Вас есть замечания к ним. Можно личным сообщением.