Гипербола: формулы, примеры решения задач
Определение гиперболы, решаем задачи вместе
Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы имеет вид:

На чертеже ниже фокусы обозначены как 

При a = b гипербола называется равносторонней.
Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.
Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:

Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.
Точки 


называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).
называется эксцентриситетом гиперболы.
Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.
Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.
Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.
То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.
Подставляем и вычисляем:
Получаем требуемое в условии задачи каноническое уравнение гиперболы:

Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет 



На чертеже расстояния обозначены оранжевыми линиями.
Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями

Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы

где 





Пример 4. Дана гипербола 
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. 

Получаем уравнение директрис гиперболы:
Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке «Эллипс» это пример 7.
Асимптоты гиперболы определяются уравнениями

Уравнение гиперболы, отнесённой к асимптотам, имеет вид:


Пример 5. Даны уравнения асимптот гиперболы 


Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:
Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.
Решить задачи на гиперболу самостоятельно, а затем посмотреть решения
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
2) действительная ось 6, расстояние между фокусами 8
3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы
Гипербола: определение, функция, формула, примеры построения
В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.
Определение и функция гиперболы
Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:
Пример 1
Дана функция y = 4 /x. Построим ее график.
Решение
Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.
Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.
| 0,5 | 8 | 1 | 4 | 2 | 2 | 4 | 1 | 8 | 0,5 |  Чтобы построить ветвь в третьей четверти, вместо x в формулу подставляем -x. Так мы вычислим значения y. Соединив полученные точки получаем следующий результат. На этом построение гиперболы завершено. Пример 2Рассмотренный выше пример был одним из самых простых (без смещения асимптот). Давайте усложним задачу и построим гиперболу, заданную функцией ниже: ГиперболаЧто такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)). Функция заданная формулой \(y=\frac Что нужно знать, чтобы построить гиперболу?
Пример №2: Находим вторую асимптоту. Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1): Находим первую асимптоту. Находим вторую асимптоту. Остается y≠1 это вторая асимптота. Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1): 3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере: Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат. 4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример: Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой. Вторая ось симметрии это прямая y=-x.
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере: а) Находим первую асимптоту. Находим вторую асимптоту. б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти. в) Возьмем несколько дополнительных точек и отметим их на графике. г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞). 7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k Category: 8 класс, База знаний, Уроки Tag: Гипербола Leave a comment Гипербола: Определение: Гиперболой называется геометрическое место точек абсолютное значение разности расстояний от которых до двух выделенных точек Получим каноническое уравнение гиперболы. Выберем декартову систему координат так, чтобы фокусы Рис. 31. Вывод уравнения гиперболы. Расстояние между фокусами (фокусное расстояние) равно Следовательно, согласно определению имеем Возведем обе части равенства в квадрат, получим Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим Проанализируем полученное уравнение. Если точка М(х;у) принадлежит гиперболе, то ей принадлежат и симметричные точки Рис. 32. Асимптоты и параметры гиперболы Определение: Найденные точки Докажем, что при возрастании (убывании) переменной х гипербола неограниченно приближается к прямым Определение: Прямые, к которым неограниченно приближается график гиперболы называются асимптотами гиперболы. Определение: Эксцентриситетом гиперболы называется отношение фокусного расстояния к действительной полуоси гиперболы Из определения эксцентриситета гиперболы следует, что он удовлетворяет неравенству Пример: Составить каноническое уравнение гиперболы, если мнимая полуось b = 5 и гипербола проходит через точку М(4; 5). Решение: Для решения задачи воспользуемся каноническим уравнением гиперболы, подставив в него все известные величины: Пример: Решение: Для определения координат фокусов и вершин эллипса преобразуем его уравнение к каноническому виду. Эллипс: Рис. 33. Параметры эллипса и гиперболы Вычислим длину мнимой полуоси Гипербола в высшей математикеРешая его относительно или одну двузначную функцию Функция При При Кривая, все точки которой имеют координаты, удовлетворяющие уравнению (3), называется гиперболой. Гипербола в силу симметрии имеет вид, указанный на рис. 37. Точки пересечения гиперболы с осью Часть гиперболы, расположенная в первой и четвертой четвертях, называется правой ветвью, а часть гиперболы, расположенная во второй и третьей четвертях, — левой ветвью. Рассмотрим прямую, заданную уравнением Умножим и разделим правую часть на Будем придавать Вследствие симметрии видно, что часть правой ветви, расположенная в четвертой четверти, будет приближаться к прямой, определяемой уравнением Прямая, к которой неограниченно приближается гипербола при удалении от начала координат, называется асимптотой гиперболы. Таким образом, гипербола имеет две асимптоты, определяемые уравнениями При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг. Теперь вы знаете какие однокоренные слова подходят к слову Как написать уравнение гиперболы по графику, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову "Как написать уравнение гиперболы по графику", предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором. |









 гипербола, где k y≠0 это вторая асимптота.
гипербола, где k y≠0 это вторая асимптота. 








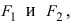
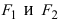
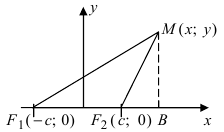
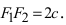 Согласно определению, для гиперболы имеем
Согласно определению, для гиперболы имеем 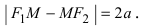 Из треугольников
Из треугольников 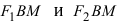 по теореме Пифагора найдем
по теореме Пифагора найдем 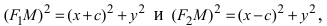 соответственно.
соответственно.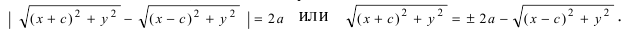
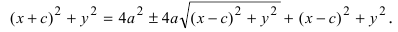
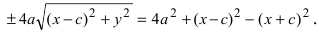 Раскроем разность квадратов
Раскроем разность квадратов 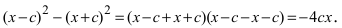 Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно перейдет в уравнение
Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно перейдет в уравнение 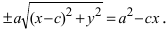 Вновь возведем обе части равенства в квадрат
Вновь возведем обе части равенства в квадрат 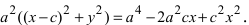 Раскрывая все скобки в правой части уравнения, получим
Раскрывая все скобки в правой части уравнения, получим 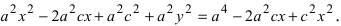 Соберем неизвестные в левой части, а все известные величины перенесем в правую часть уравнения, получим
Соберем неизвестные в левой части, а все известные величины перенесем в правую часть уравнения, получим 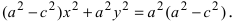 Введем обозначение для разности, стоящей в скобках
Введем обозначение для разности, стоящей в скобках 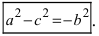 Получим
Получим 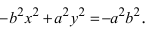 Разделив все члены уравнения на величину
Разделив все члены уравнения на величину 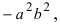 получаем каноническое уравнение гиперболы:
получаем каноническое уравнение гиперболы: 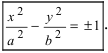 Для знака “+” фокусы гиперболы расположены на оси Ох, вдоль которой вытянута гипербола. Для знака фокусы гиперболы расположены на оси Оу, вдоль которой вытянута гипербола.
Для знака “+” фокусы гиперболы расположены на оси Ох, вдоль которой вытянута гипербола. Для знака фокусы гиперболы расположены на оси Оу, вдоль которой вытянута гипербола.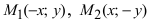 и
и 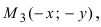 следовательно, гипербола симметрична относительно координатных осей, которые в данном случае будут называться осями симметрии гиперболы (Рис. 32). Найдем координаты точек пересечения гиперболы с координатными осями:
следовательно, гипербола симметрична относительно координатных осей, которые в данном случае будут называться осями симметрии гиперболы (Рис. 32). Найдем координаты точек пересечения гиперболы с координатными осями: 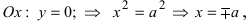 т.е. точками пересечения гиперболы с осью абсцисс будут точки
т.е. точками пересечения гиперболы с осью абсцисс будут точки 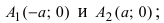
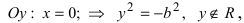 т.е. гипербола не пересекает ось ординат.
т.е. гипербола не пересекает ось ординат.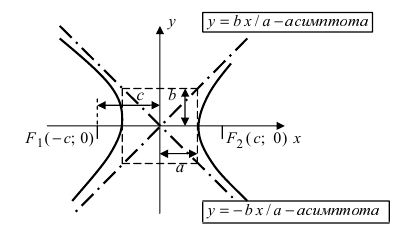
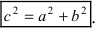
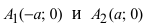 называются вершинами гиперболы.
называются вершинами гиперболы.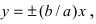 не пересекая эти прямые. Из уравнения гиперболы находим, что
не пересекая эти прямые. Из уравнения гиперболы находим, что 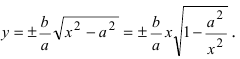 При неограниченном росте (убывании) переменной х величина
При неограниченном росте (убывании) переменной х величина 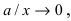 следовательно, гипербола будет неограниченно приближаться к прямым
следовательно, гипербола будет неограниченно приближаться к прямым 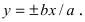
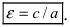
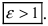 Кроме того, эта характеристика описывает форму гиперболы. Для демонстрации этого факта рассмотрим квадрат отношения мнимой полуоси гиперболы к действительной полуоси
Кроме того, эта характеристика описывает форму гиперболы. Для демонстрации этого факта рассмотрим квадрат отношения мнимой полуоси гиперболы к действительной полуоси 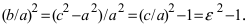 Если эксцентриситет
Если эксцентриситет 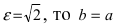 и гипербола становится равнобочной. Если
и гипербола становится равнобочной. Если 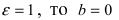 и гипербола вырождается в два полубесконечных отрезка
и гипербола вырождается в два полубесконечных отрезка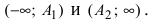
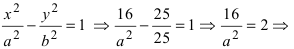
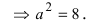 Следовательно, каноническое уравнение гиперболы имеет вид
Следовательно, каноническое уравнение гиперболы имеет вид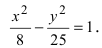
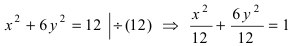 или
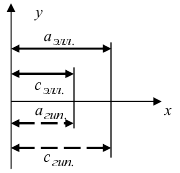
или 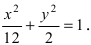 Следовательно, большая полуось эллипса
Следовательно, большая полуось эллипса 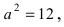 а малая полуось
а малая полуось 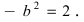 Итак, вершины эллипса расположены на оси
Итак, вершины эллипса расположены на оси 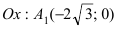 и
и 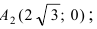 на оси
на оси 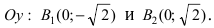 Так как
Так как  то эллипс вытянут вдоль оси абсцисс Ох. Определим расположение фокусов данного эллипса
то эллипс вытянут вдоль оси абсцисс Ох. Определим расположение фокусов данного эллипса 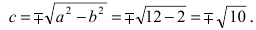 Итак,
Итак, 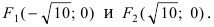 Согласно условию задачи (см. Рис. 33):
Согласно условию задачи (см. Рис. 33): 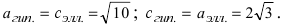
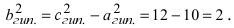 Уравнение гиперболы имеет вид:
Уравнение гиперболы имеет вид: 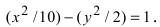

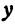 , получим две явные функции
, получим две явные функции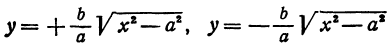
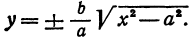
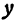 имеет действительные значения только в том случае, если
имеет действительные значения только в том случае, если  . При
. При 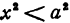 функция
функция 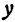 действительных значений не имеет. Следовательно, если
действительных значений не имеет. Следовательно, если 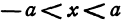 , то точек с координатами, удовлетворяющими уравнению (3), не существует.
, то точек с координатами, удовлетворяющими уравнению (3), не существует.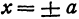 получаем
получаем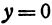 .
.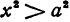 каждому значению
каждому значению 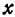 соответствуют два значения
соответствуют два значения 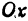 . Так же можно убедиться в симметрии относительно оси
. Так же можно убедиться в симметрии относительно оси 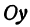 . Поэтому в рассуждениях можно ограничиться рассмотрением только первой четверти. В этой четверти при увеличении х значение у будет также увеличиваться (рис. 36).
. Поэтому в рассуждениях можно ограничиться рассмотрением только первой четверти. В этой четверти при увеличении х значение у будет также увеличиваться (рис. 36).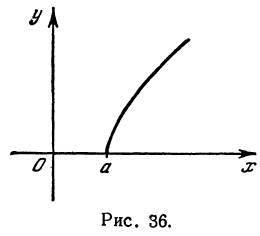
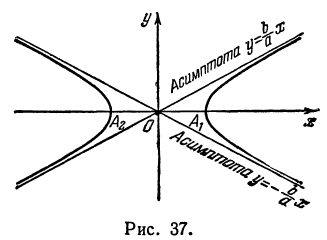
 называются вершинами гиперболы; на рис. 37 они обозначены буквами
называются вершинами гиперболы; на рис. 37 они обозначены буквами 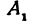 и
и 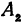 .
.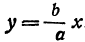 . Чтобы не смешивать ординату точки, расположенной на этой прямой, с ординатой точки, расположенной на гиперболе, будем обозначать ординату точки на прямой
. Чтобы не смешивать ординату точки, расположенной на этой прямой, с ординатой точки, расположенной на гиперболе, будем обозначать ординату точки на прямой 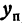 , а ординату точки на гиперболе через
, а ординату точки на гиперболе через 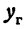 . Тогда
. Тогда 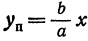 ,
, 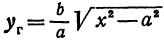 (рассматриваем только кусок правой ветви, расположенной в первой четверти). Найдем разность ординат точек, взятых на прямой и на гиперболе при одинаковых абсциссах:
(рассматриваем только кусок правой ветви, расположенной в первой четверти). Найдем разность ординат точек, взятых на прямой и на гиперболе при одинаковых абсциссах: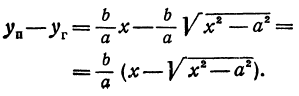
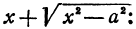
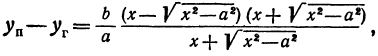
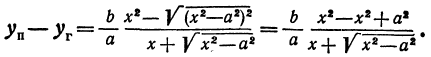
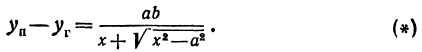
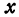 все большие и большие значения, тогда правая часть равенства
все большие и большие значения, тогда правая часть равенства 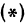 будет становиться все меньше и меньше, приближаясь к нулю. Следовательно, разность
будет становиться все меньше и меньше, приближаясь к нулю. Следовательно, разность  будет приближаться к нулю, а это значит, что точки, расположенные на прямой и гиперболе, будут сближаться. Таким образом, можно сказать, что рассматриваемая часть правой ветви гиперболы по мере удаления от начала координат приближается к прямой
будет приближаться к нулю, а это значит, что точки, расположенные на прямой и гиперболе, будут сближаться. Таким образом, можно сказать, что рассматриваемая часть правой ветви гиперболы по мере удаления от начала координат приближается к прямой 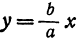 .
.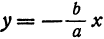 . Также кусок левой ветви, расположенный во второй четверти, приближается к прямой
. Также кусок левой ветви, расположенный во второй четверти, приближается к прямой 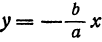 , а кусок левой ветви, расположенный в третьей четверти, — к прямой
, а кусок левой ветви, расположенный в третьей четверти, — к прямой 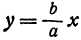 .
. (рис. 37).
(рис. 37).