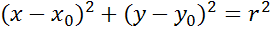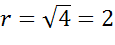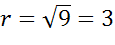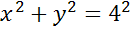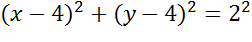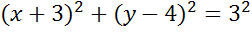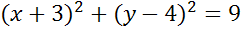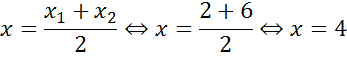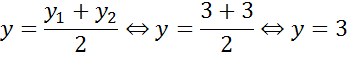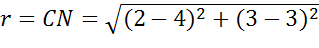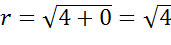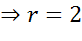Уравнение окружности
Урок 16. Геометрия 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Уравнение окружности»
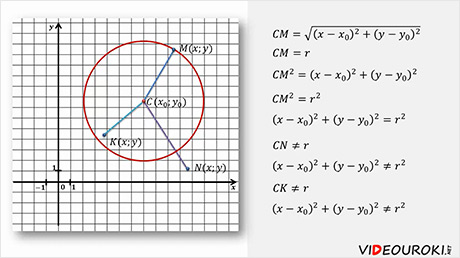
Прежде всего, давайте вспомним, формулу расстояния между двумя точками и еще, повторим, что уравнение с двумя переменными x и y называется уравнением линии l, если этому уравнению удовлетворяют координаты любой точки линии l и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
Сегодня на уроке мы попробуем по геометрическим свойствам линии найти ее уравнение.
В качестве линии рассмотрим окружность радиуса 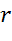
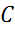
Задача. Записать уравнение окружности с радиусом 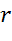
Начало координат имеет координаты (0;0). Подставим их в уравнение окружности и получим, что уравнение окружности с радиусом r и центром в начале координат имеет вид
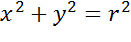
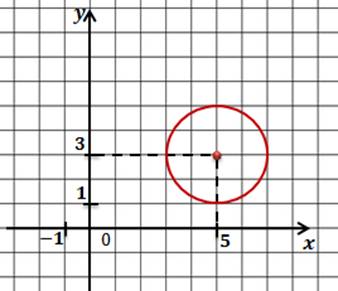
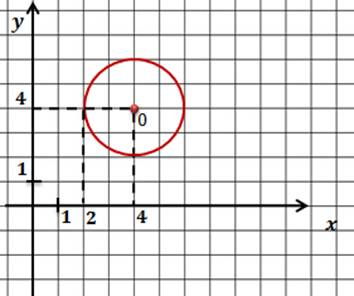
Задача. Начертить окружность, заданную уравнением 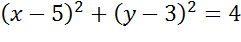
Запишем общее уравнение окружности и проанализируем исходное уравнение. Прежде всего, определимся с координатами центра окружности. Это будут числа 5 и 3. Теперь давайте определим величину радиуса окружности.
Поскольку в правой части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень из 4. Получим 2.
Значит наша формула задает окружность с центром в точке с координатами пять три и радиусом равным двум.
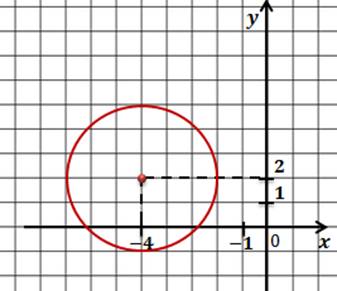
Задача. Начертить окружность, заданную уравнением 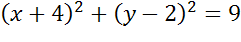
Запишем общее уравнение окружности и проанализируем исходное уравнение. Прежде всего определимся с координатами центра окружности.
Задача. Начертить окружность, заданную уравнением 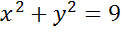
Решение. Уравнениями такого типа описываются окружности с центром в начале координат. Теперь давайте определим величину радиуса окружности. Поскольку в правой части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень из 9.
Значит наша формула задает окружность с центром в точке с координатами (0;0) и радиусом равным 3.
Теперь давайте попробуем решить задачу обратную данным.
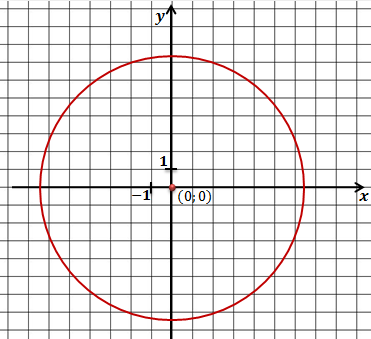
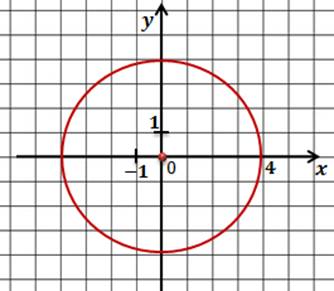
Задача. Составить уравнение окружности, которая показана на рисунке.
Как и в предыдущих задачах мы начнем с определения координат центра окружности. Сделать это нетрудно. Центр этой окружности совпадает с началом координат, поэтому центр окружности имеет координаты (0;0).
Нетрудно заметить, что радиус окружности равен 4.
Запишем уравнение окружности и подставим найденные значения.
Ответ: 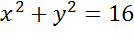
Решим еще одну задачу.
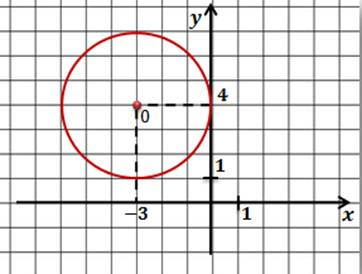
Задача. Составить уравнение окружности, которая показана на рисунке.
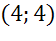
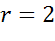
Ответ: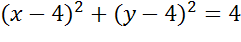
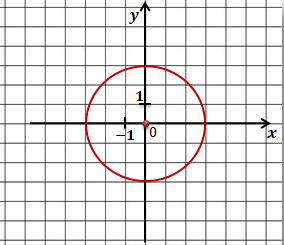
Задача. Составить уравнение окружности, которая показана на рисунке.
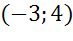
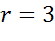
Ответ: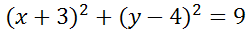
Решая задачи, мы с вами выполняли один и тоже порядок действий. Давайте еще раз повторим этот порядок.
Для того, что бы составить уравнение окружности и построить ее надо:
1. Найти координаты центра окружности.
2. Найти длину радиуса этой окружности.
3. Записать уравнение окружности.
4. Подставить полученные значения в уравнение окружности.
5. Построить окружность, если это требуется для решения задачи.
Рассмотрим еще одну задачу.
Написать уравнение окружности с диаметром эм эн, если точка эн имеет координаты два три, точка эм имеет координаты шесть три.
Задача. Написать уравнение окружности с диаметром 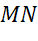
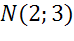
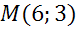
Найдем координаты центра окружности. Центр окружности является серединой диаметра. Воспользуемся формулами для нахождения координат середины отрезка.
Получим, что центр окружности имеет координаты 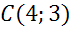
Теперь определим радиус окружности. Для этого найдем расстояние от центра окружности до концов диаметра.
Запишем общее уравнение окружности и подставим в него найденные значения. Тогда получим, что уравнение данной окружности имеет вид:
Ответ: 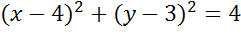
Подведем итоги урока.
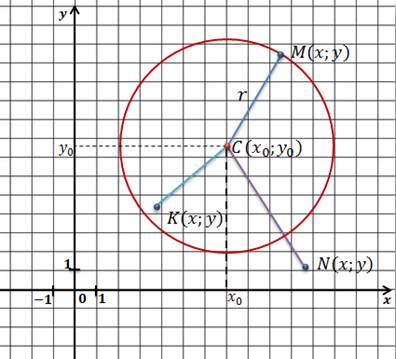
На сегодняшнем уроке мы познакомились с формулой, которая задает окружность с центром в точке С (x0; y0) и радиусом r.
Также мы познакомились с формулой, которая задает окружность с центром в начале координат и радиусом r.
Мы рассмотрели задачи на составление уравнения окружности по рисунку и на построение окружности по заданному уравнению.
Урок по геометрии уравнение окружности 9 класс
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Выбранный для просмотра документ #U041e#U043a#U0440#U0443#U0436#U043d#U043e#U0441#U0442#U044c 9 #U043a#U043b#U0430#U0441#U0441.ppt
Описание презентации по отдельным слайдам:
Окружность – геометрическая фигура, состоящая из всех точек плоскости, равноудаленных от данной точки плоскости. Пусть d – расстояние от центра окружности до заданной точки плоскости, R – радиус окружности d R Точка лежит внутри окружности Точка принадлежит окружности Точка лежит вне окружности R = 5 cм R = 7 см R = 12 cм ОА = 3 cм ОК = 7 см ОС > 12 см
Уравнение окружности О (хо, уо) – центр окружности, А (х; у) – точка окружности
Задачи № 1 Заполнить таблицу по следующим данным: 2 2 2 2 2 2 2 2 2 2 Координаты центра окружности Радиус окружности Уравнение окружности (0; 0) 7 х + у = 49 (-1; 4) 6 (х + 1) + (у – 4) = 36 (4; 1,5) 10 (х – 4) + (у – 1,5) = 100 (-12; 0) 2 корня из 2 (х + 12) + у = 8 (-2; 3) 9 (2 + х) + (3 – у) = 81
Задачи № 2 Вывести уравнение окружности с центром в точке М (-3; 4), проходящей через начало координат. Дано: М (-3; 4) – центр окружности О (0; 0) – точка на окружности
Решить № 959 (устно), 960 (б), 961 (А, В, D), 962, 964, 966 (а) Домашнее задание П. 91 № 965, 966 (б, в, г), 968
Выбранный для просмотра документ #U0423#U0440#U043e#U043a1.ppt
Описание презентации по отдельным слайдам:
Урок геометрии в 9 классе
Цели урока: Образовательные: Вывести уравнение окружности, рассмотрев решение этой задачи как одну из возможностей применения метода координат. Уметь: – Распознать уравнение окружности по предложенному уравнению, научить учащихся составлять уравнение окружности по готовому чертежу, строить окружность по заданному уравнению. –Применять современные ИКТ для оформления результатов исследования. Воспитательные: Формирование критического мышления. Развивающие: Развитие умения составлять алгоритмические предписания и умение действовать в соответствии с предложенным алгоритмом.
Повторение Запишите формулу нахождения координат середины отрезка. Запишите формулу вычисления длины вектора. Запишите формулу нахождения расстояния между точками (длины отрезка).
Формула I (х – а)2 + (у – b)2 = R2 уравнение окружности, где А(а;b) − центр, R − радиус, х и у – координаты точки окружности. __________________________ А(2;4) – центр, R = 3, то (х – 2)2 + (у – 4)2 = 32; (х – 2)2 + (у – 4)2 = 9.
Для того чтобы составить уравнение окружности, нужно: Задачи
№1. Составить уравнение окружности. координаты центра: ( ; ) R = уравнение окружности:
№2. Составить уравнение окружности. координаты центра: ( ; ) R = уравнение окружности:
№3. Составить уравнение окружности.
№4. Составить уравнение окружности.
Задача: Напишите уравнение окружности с центром в начале координат и диаметром 8. Так как диаметр окружности в два раза больше её радиуса, то r=8÷2=4. Поэтому х²+у²=16.
Постройте в тетради окружности, заданные уравнениями: 1) (х – 5)2 + (у + 3)2 = 9; 2) (х + 1)2 + (у – 7)2 = 16.
Составьте уравнение окружности с центром А(3;2), проходящей через В(7;5).
Заполните таблицу. № Уравнение окружности Радиус Коорд. центра 1 (х – 5)2 + (у + 3)2 = 36 R= ( ; ) 2 (х – 1)2 + (у + 1)2 = 2 R= ( ; ) 3 (х + 1)2 + (у – 7)2 = 49 R= ( ; ) 4 х2 + у2 = 81 R= ( ; ) 5 (у – 5)2 + (х + 3)2 = 7 R= ( ; ) 6 (х + 3)2 + у2 = 14 R= ( ; )
Домашнее задание: §3, п.91, контрольные вопросы №16,17. Задачи №959(б, г, д), 967. Задача на дополнительную оценку (проблемная задача): Построить окружность, заданную уравнением: х²+2х+у²-4у=4.
Выбранный для просмотра документ #U0443#U0440#U043e#U043a #U0443#U0440#U0430#U0432#U043d#U0435#U043d#U0438#U0435 #U043e#U043a#U0440#U0443#U0436#U043d#U043e#U0441#U0442#U0438 #U0433#U0435#U043e#U043c#U0435#U0442#U0440#U0438#U044f.doc
Тема урока: Уравнение окружности
Образовательные: Вывести уравнение окружности, рассмотрев решение этой задачи как одну из возможностей применения метода координат.
– Распознать уравнение окружности по предложенному уравнению, научить учащихся составлять уравнение окружности по готовому чертежу, строить окружность по заданному уравнению.
Воспитательные : Формирование критического мышления.
Развивающие : Развитие умения составлять алгоритмические предписания и умение действовать в соответствии с предложенным алгоритмом.
– Видеть проблему и наметить пути её решения.
– Кратко излагать свои мысли устно и письменно.
Тип урока: усвоения новых знаний.
Оборудование : ПК, мультимедийный проектор, экран.
1. Вступительное слово – 3 мин.
2. Актуализация знаний – 2 мин.
3. Постановка проблемы и её решение –10 мин.
4. Фронтальное закрепление нового материала – 7 мин.
5. Самостоятельная работа в группах – 15 мин.
6. Презентация работы: обсуждение – 5 мин.
7. Итог урока. Домашнее задание – 3 мин.
Цель данного этапа: Психологический настрой учащихся; Вовлечение всех учащихся в учебный процесс, создание ситуации успеха.
1. Организационный момент.
-Ребята! С окружностью вы познакомились ещё в 5 и 8 классах. А что вы о ней знаете?
-Знаете вы много, и эти данные можно использовать при решении геометрических задач. Но для решения задач, в которых применяется метод координат, этого недостаточно. Почему?
Поэтому главной целью сегодняшнего урока я ставлю выведение уравнения окружности по геометрическим свойствам данной линии и применение его для решения геометрических задач.
Записывают тему урока в тетрадь.
-Мы ещё не знаем общего вида уравнения окружности.
Учащиеся перечисляют все, что знают об окружности.
Цель этапа – получить представление о качестве усвоения учащимися материала, определить опорные знания.
2. Актуализация знаний.
При выведении уравнения окружности вам потребуются уже известное определение окружности и формула, позволяющая найти расстояние между двумя точками по их координатам. Давайте вспомним эти факты /п овторение материала, изученного ранее/:
– Запишите формулу нахождения координат середины отрезка.
– Запишите формулу вычисления длины вектора.
– Запишите формулу нахождения расстояния между точками (длины отрезка).
Даны точки А (-1;7) и В (7; 1).
Вычислите координаты середины отрезка АВ и его длину.
Проверяет правильность выполнения, корректирует расчеты…
— Один ученик у доски, а остальные в тетрадях записывают формулы
-Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.
3. Формирование новых знаний.
-Будут ли координаты любой другой точки удовлетворять данному равенству? Почему?
Возведём обе части равенства в квадрат. В результате имеем:
r² =(х –х )²+(у –у )²-уравнение окружности, где (х ;у )-координаты центра окружности, (х ;у )-координаты произвольной точки лежащей на окружности, r-радиус окружности.
Какой вид будет иметь уравнение окружности с центром в начале координат?
Итак, что надо знать для составления уравнения окружности?
Предложите алгоритм составления уравнения окружности.
Вывод: … записать в тетрадь.
-Радиусом называется отрезок, соединяющий центр окружности с произвольной точкой лежащей на окружности. Поэтому r=|АМ|=√(х –х )²+(у –у )²
-Любая точка окружности лежит на этой окружности.
Учащиеся ведут записи в тетради.
(0;0)-координаты центра окружности.
х²+у²=r², где r-радиус окружности.
-координаты центра окружности, радиус, любую точку окружности…
Записывают алгоритм в тетрадь.
Учитель фиксирует равенство на доске.
Учитель фиксирует равенство на доске.
4. Первичное закрепление.
-Применим полученные знания при решении следующих задач.
Задача: Из предложенных уравнений назовите номера тех, которые являются уравнениями окружности. И если уравнение является уравнением окружности, то назовите координаты центра и укажите радиус.
-Не каждое уравнение второй степени с двумя переменными задаёт окружность.
4х²+у²=4- уравнение эллипса.
х²+у²=-4- это уравнение не задаёт никакой фигуры.
-Ребята! А что нужно знать, чтобы составить уравнение окружности?
Решите задачу №966 стр.245(учебник).
Учитель вызывает ученика к доске.
-Достаточно ли данных, которые указаны в условии задачи, чтобы составить уравнение окружности?
Напишите уравнение окружности с центром в начале координат и диаметром 8.
Задача : построение окружности.
— Центр имеет координаты?
— Определите радиус… и выполняйте построение
Задача на стр.243 (учебник) разбирается устно.
Используя план решения задачи со стр.243, решите задачу:
Составьте уравнение окружности с центром в точке А(3;2), если окружность проходит через точку В(7;5).
1) (х-5)²+(у-3)²=36- уравнение окружности;(5;3),r=6.
2) (х-1)²+у²=49- уравнение окружности;(1;0),r=7.
3) х²+у²=7- уравнение окружности;(0;0),r=√7.
4) (х+3)²+(у-8)²=2- уравнение окружности; (-3;8),r=√2.
5) 4х²+у²=4-не является уравнением окружности.
6) х²+у²=0- не является уравнением окружности.
7) х²+у²=-4- не является уравнением окружности.
-Знать координаты центра окружности.
-Подставить координаты центра и длину радиуса в уравнение окружности общего вида.
Решают задачу № 966 стр.245(учебник).
-Так как диаметр окружности в два раза больше её радиуса, то r=8÷2=4. Поэтому х²+у²=16.
— Выполняют построение окружностей
Работа по учебнику. Задача на стр.243.
Дано: А(3;2)-центр окружности; В(7;5)є(А;r)
Найти: уравнение окружности
Решение типовых задач, проговаривая способ решения в громкой речи.
Учитель вызывает одного ученика записать полученное уравнение.
Возврат к слайду 9
Обсуждение плана решения данной задачи.
Слайд. 15. Учитель вызывает одного ученика к доске решать данную задачу.
Рефлексия деятельности на уроке.
Домашнее задание: §3, п.91, контрольные вопросы №16,17.
Задачи № 959(б, г, д), 967.
Задача на дополнительную оценку (проблемная задача): Построить окружность, заданную уравнением
-О чём на уроке мы говорили?
-Что хотели получить?
-Какая цель была поставлена на уроке?
-Какие задачи позволяет решить сделанное нами «открытие»?
-Кто из вас считает, что достиг цели, поставленной на уроке учителем на100%, на 50%; не достиг цели…?
Записывают домашнее задание.
Учащиеся отвечают на поставленные учителем вопросы. Проводят самоанализ собственной деятельности.
Учащимся необходимо выразить в слове результат и способы достижения.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-180957
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ
Время чтения: 1 минута
Во всех педвузах страны появятся технопарки
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Большинство родителей в России удовлетворены качеством образования в детсадах
Время чтения: 2 минуты
Ученые изучили проблемы родителей, чьи дети учатся в госпитальных школах
Время чтения: 5 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.