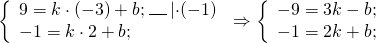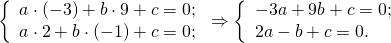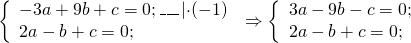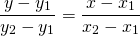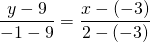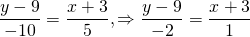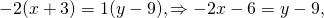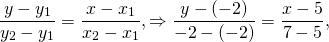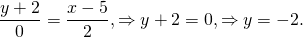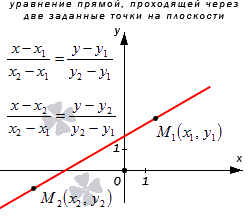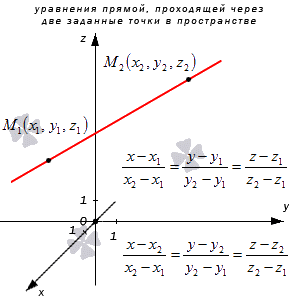Составить уравнение прямой, проходящей через две точки
Рассмотрим, как составить уравнение прямой, проходящей через две точки, на примерах.
Составить уравнение прямой, проходящей через точки A(-3; 9) и B(2;-1).
1 способ — составим уравнение прямой с угловым коэффициентом.
2 способ — составим общее уравнение прямой.
Общее уравнение прямой имеет вид ax+by+c=0. Подставив координаты точек A и B в уравнение, получаем систему:
Поскольку количество неизвестных больше количества уравнений, система не разрешима. Но можно все переменные выразить через одну. Например, через b.
получим: 5a-10b=0. Отсюда a=2b.
2bx+by-3b=0. Осталось разделить обе части на b:
Общее уравнение прямой легко приводится к уравнению прямой с угловым коэффициентом:
3 способ — составим уравнение прямой, проходящей через 2 точки.
Уравнение прямой, проходящей через две точки, имеет вид:
Подставим в это уравнение координаты точек A(-3; 9) и B(2;-1)
В школьном курсе чаще всего используется уравнение прямой с угловым коэффициентом. Но самый простой способ — вывести и использовать формулу уравнения прямой, проходящей через две точки.
Если при подстановке координат заданных точек один из знаменателей уравнения
окажется равным нулю, то искомое уравнение получается приравниваем к нулю соответствующего числителя.
Подставляем в уравнение прямой, проходящей через 2 точки, координаты точек C и D:
Составить уравнение прямой, проходящей через точки M (7; 3) и N (7; 11).
Уравнение прямой, которая проходит через две заданные точки: примеры, решения
Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.
Уравнение прямой, проходящей через две заданные точки на плоскости
Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.
Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.
Рассмотрим рисунок, приведенный ниже.
Рассмотрим подробней на решении нескольких примеров.
При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.
Приведем каноническое уравнение к искомому виду, тогда получим:
Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.
При подстановке получаем, что
Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.
Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве
Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.
Прямая линия. Уравнение прямой.
Свойства прямой в евклидовой геометрии.
Через любую точку можно провести бесконечно много прямых.
Через любые две несовпадающие точки можно провести единственную прямую.
Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются
параллельными (следует из предыдущего).
В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия
задается на плоскости уравнением первой степени (линейное уравнение).
Общее уравнение прямой.
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим
уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• В = 0, А ≠0, С ≠ 0 – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных
Уравнение прямой по точке и вектору нормали.
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В)
подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно
Уравнение прямой, проходящей через две точки.
проходящей через эти точки:
Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На
плоскости записанное выше уравнение прямой упрощается:
Дробь 
Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
Решение. Применяя записанную выше формулу, получаем:
Уравнение прямой по точке и угловому коэффициенту.
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
и обозначить 
уравнением прямой с угловым коэффициентом k.
Уравнение прямой по точке и направляющему вектору.
По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание
прямой через точку и направляющий вектор прямой.
Определение. Каждый ненулевой вектор 
Аα1 + Вα2 = 0 называется направляющим вектором прямой.
Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением,
коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В.
Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.
Уравнение прямой в отрезках.
Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:


Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения
прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
Нормальное уравнение прямой.
Если обе части уравнения Ах + Ву + С = 0 разделить на число 
нормирующем множителем, то получим
Общее уравнение прямой: описание, примеры, решение задач
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.
Общее уравнение прямой: основные сведения
указанная теорема состоит из двух пунктов, докажем каждый из них.
Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Рассмотрим конкретный пример общего уравнения прямой.
Неполное уравнение общей прямой
Разберем все вариации неполного общего уравнения прямой.
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.
Решение
На чертеже изображена прямая, необходимо записать ее уравнение.
Решение
Общее уравнение прямой, проходящей через заданную точку плоскости
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Решение
Решение
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Решение
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Решение
Осуществим переход от общего уравнения к каноническому:
Решение
Произведем нужные действия по алгоритму:
Решение
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
Каноническое уравнение преобразуется к общему по следующей схеме:
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
Решение
Осуществим переход от параметрических уравнений к каноническому:
Перейдем от канонического к общему:
Решение:
Просто перепишем уравнение в необходимом виде:
Составление общего уравнения прямой
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Решение
Решение
Уравнение прямой
Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
Уравнение прямой в отрезках на осях
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x 0 y = m t + y 0
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a =
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
 | x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n =
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений