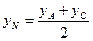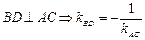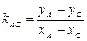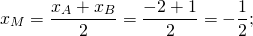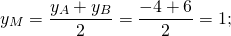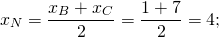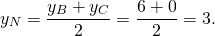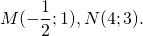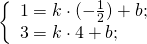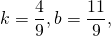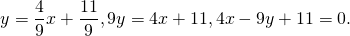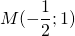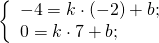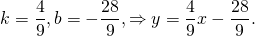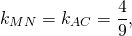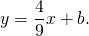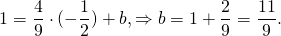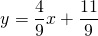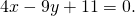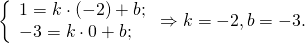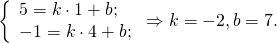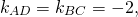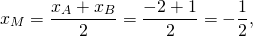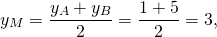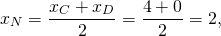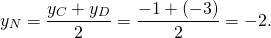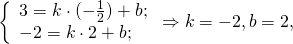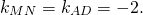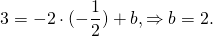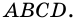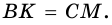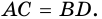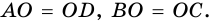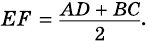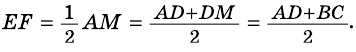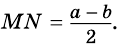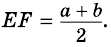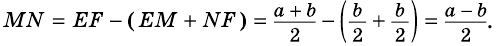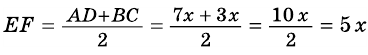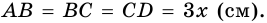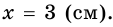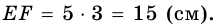Написать уравнение сторон равнобедренной трапеции
Линейные образы на плоскости и в пространстве: Написать уравнение сторон равнобедренной трапеции
Написать уравнение сторон равнобедренной трапеции, зная середины ее оснований (1;1), (2;8) и точки.

в равнобедренной трапеции боковая сторона с=13 а основания а=21 b=11 вычислить длину диолонали.
Периметр равнобедренной трапеции по основанию и углу
Условие задачи следующее: В равнобедренной трапеции меньшая основа=боковой стороне,большая.

Имеется равнобокая трапеция ABMN, которая вписана в окружность. Так же известно, что на нижнем.
Далее, координаты середины М отрезка АВ равны полусумме координат его концов; отсюда М((х+4)/2,(у-3)/2). Так как М лежит на прямой L, то
7(х+4)/2-(у-3)/2-6=0. (Это второе уравнение.)
Решайте систему для вычисления координат точки В.
Добавлено через 13 минут
Чтобы не заморачиваться с точкой М на прямой, формулу можно ещё упростить:
Написать уравнение трёх сторон квадрата
1) Дана одна из сторон квадрата АВ х+3у-3=0 и дана точка М(-2;0) пересечения его диагоналей d1 и.
Найти уравнения боковых сторон трапеции
Не могу справиться с заданием! Решения подобных задач тоже не нахожу..

Помогите пожалуйста решить задачу: Найти длину боковой стороны равнобедренной трапеции с углом при.
Задача 7. Равнобедренная трапеция с основаниями 10 и 4 единиц имеет острый угол 300.



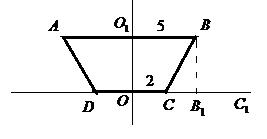
Написать уравнения сторон трапеции, приняв за ось ОХ меньшее основание трапеции,
а за ось ОУ ось симметрии трапеции
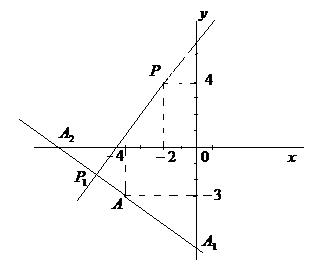
Замечание. К задаче 3 удобнее записать краткие условия после выполнения чертежа
АВСD –равнобедренная трапеция,
DC – меньшее основание, ось ОУ – ось симметрии трапеции
Составить уравнения сторон
1Составим уравнение стороны DC (рис.7)
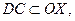
2 Составим уравнение стороны СВ
Т.к по условию трапеция равнобедренная, то 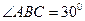
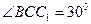
(углы равны как внутренние на крест лежащие), следовательно 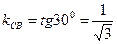
По условию ОУ ось симметрии трапеции, тогда
Воспользуемся уравнением «пучка»
3 Составим уравнение стороны АD
По условию трапеция равнобедренная, то 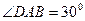
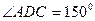
По условию ОУ ось симметрии трапеции, тогда 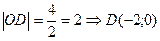
Воспользуемся уравнением «пучка»
4 Составим уравнение стороны АВ
4.1 Найдем координаты точки В:
по условию ОУ ось симметрии трапеции, тогда 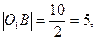
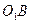
(рис.7) равна 5, тогда 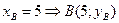
Точка В лежит на прямой СВ, её координаты удовлетворяют уравнению СВ:
4.2 Составим уравнение стороны АВ:
Воспользуемся уравнением «пучка»
Ответ:
Найти проекцию точки 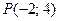
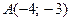
1 Составим уравнение прямой 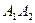
Т.к. по условию прямая 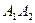
воспользуемся уравнений прямой в «отрезках». Пусть 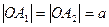
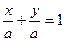
Точка А(-4;-3) лежит на прямой 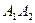
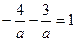
Подставим в уравнение (*)
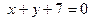
2 Составим уравнение 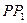
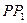
Из уравнения (**) имеем: 
Воспользуемся уравнением «пучка»
3 Найдем
Ответ:
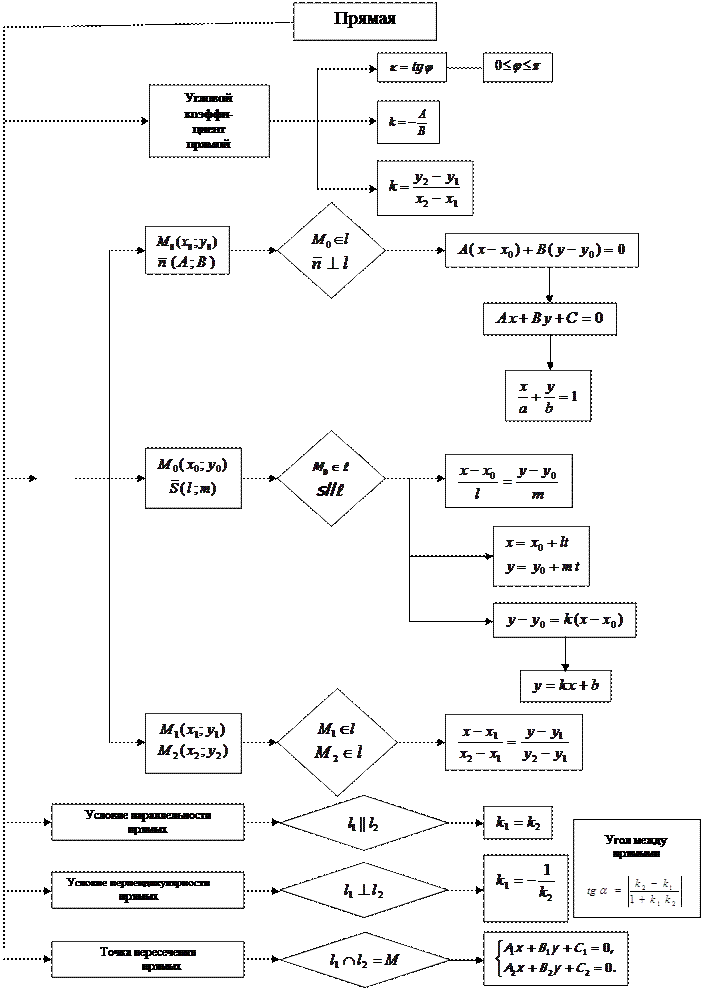
Приложение А
Основные уравнения прямой на плоскости

Приложение Б
Приложение А
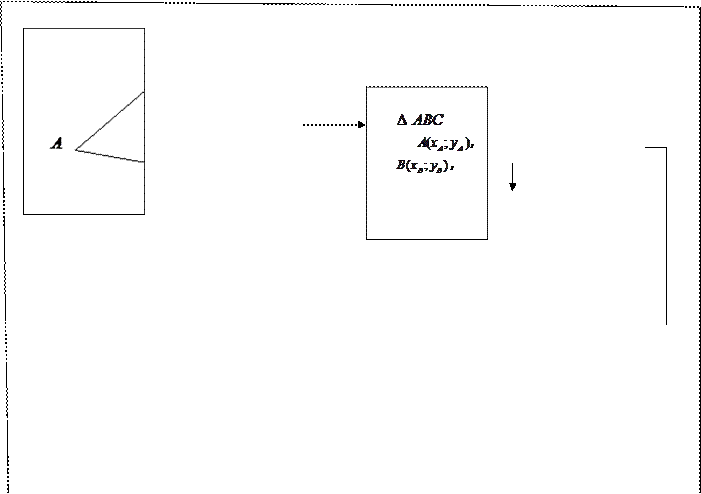
Составление уравнения медианы треугольника
|
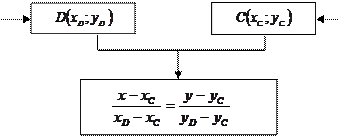 |
 |
 |
Приложение В
Составление уравнения средней линии треугольника
|
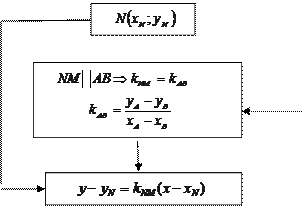 |
 |
 |
Приложение Г
Составление уравнения высоты треугольника
|
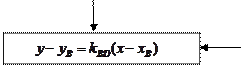 |
 |
 |
Приложение Д
Составление уравнения биссектрисы треугольника
Уравнение средней линии
Как составить уравнение средней линии треугольника по координатам его вершин? Как записать уравнение средней линии трапеции?
Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.
Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.
1) Написать уравнение прямой, содержащей среднюю линию треугольника с вершинами в точках A(-2;-4), B(1;6), C(7;0), пересекающей стороны AB и BC в точках M и N.
М — середина отрезка AB, N — середина BC.
Составим уравнение прямой MN, например, в виде y=kx+b:
Найти координату одной из точек средней линии и составить уравнение прямой, параллельной стороне треугольника.
— середина отрезка AB. Составим уравнение прямой AC:
Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.
Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:
то есть уравнение прямой MN ищем в виде
Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:
Таким образом, уравнение прямой MN
Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.
Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).
Сначала следует определить основания данной трапеции.
Составим уравнения сторон AD и BC. Если эти прямые параллельны, то AD и BC — основания трапеции. Если эти прямые не параллельны, то основания трапеции — AB и CD.
Поскольку угловые коэффициенты прямых равны:
то AD ∥BC, то есть AD и BC являются основаниями трапеции ABCD. Значит AB и CD — боковые стороны. Найдём координаты точек M и N — середины AB и CD соответственно.
Составим уравнение прямой MN, M(-1/2;3), N(2;-2):
Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:
Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.
Трапеция и ее свойства с определением и примерами решения
Содержание:
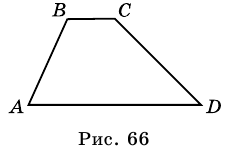
Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
На рисунке 66 изображена трапеция
Свойства трапеции
Рассмотрим некоторые свойства трапеции.
1. Сумма углов трапеции, прилежащих к боковой стороне, равна 180°.
Так как 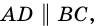
2. Трапеция является выпуклым четырехугольником.
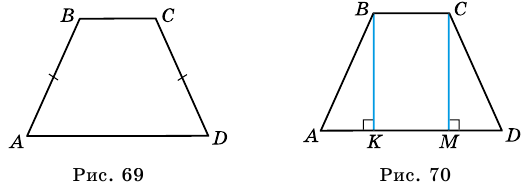
Высотой трапеции называют перпендикуляр, проведенный из любой точки основания трапеции к прямой, содержащей другое ее основание.
Как правило, высоту трапеции проводят из ее вершины. На рисунке 67 
Свойства равнобокой трапеции
Рассмотрим некоторые важные свойства равнобокой трапеции.
1. В равнобокой трапеции углы при основании равны.
Доказательство:
1) Пусть в трапеции 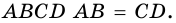
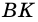
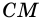
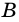
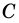
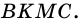
2) 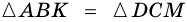
3) Также 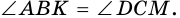
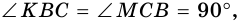
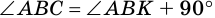
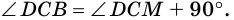
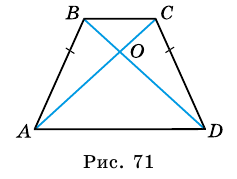
2. Диагонали равнобокой трапеции равны.
Доказательство:
Рассмотрим рисунок 71. 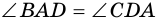
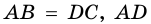
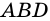
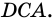
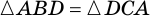
Пример:
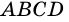
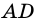
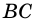
Доказательство:
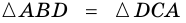
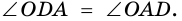
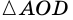
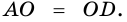
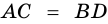
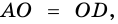
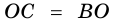
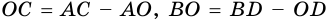
Теорема (признак равнобокой трапеции). Если в трапеции углы при основании равны, то трапеция — равнобокая.
Доказательство:
1) Пусть в 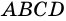
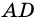
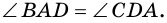
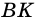
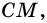
2) Тогда 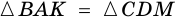
В «Началах» Евклид под термином «трапеция» подразумевал любой четырехугольник, не являющийся параллелограммом. Большинство математиков Средневековья использовали термин «трапеция» с тем же смыслом.
Свойство средней линии трапеции
Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.
Рассмотрим свойство средней линии трапеции.
Теорема (свойство средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть 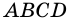
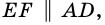
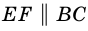
1) Проведем луч 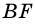
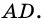
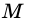
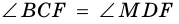
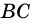
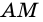
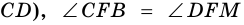
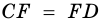
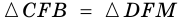
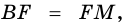
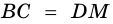
2) Поскольку 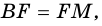
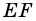
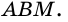
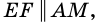
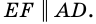
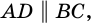
3) Кроме того,
Пример:
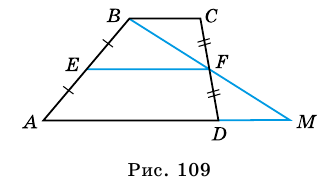
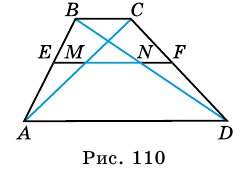
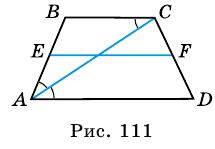
Докажите, что отрезок средней линии трапеции, содержащийся между ее диагоналями, равен полуразности оснований.
Доказательство:
Пусть 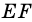
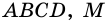
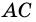
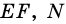
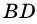
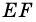
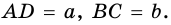
1) Так как 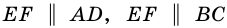
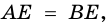
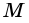
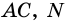
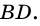
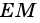
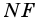
Тогда
2) 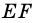
3)
Пример:
Решение:
Пусть 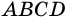
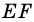
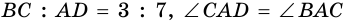
1) Обозначим 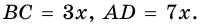
2) 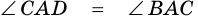
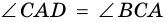
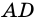
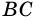
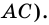
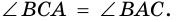
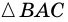
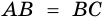
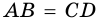
3) Учитывая, что 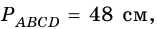
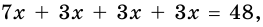
4) Тогда
То, что средняя линия трапеции равна полусумме оснований, было известно еще древним египтянам; эту информацию содержал папирус Ахмеса (примерно XVII в. до н. э.).
О свойстве средней линии трапеции знали также и вавилонские землемеры; это свойство упоминается и в трудах Герона Александрийского (первая половина I в. н. э.).
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.


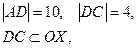
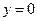
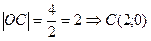
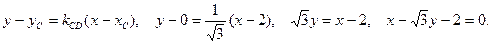
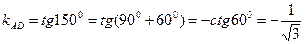
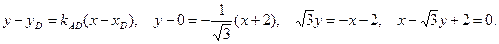
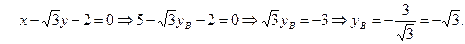
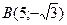
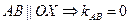
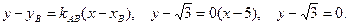
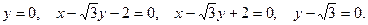
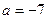
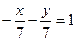
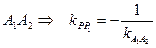
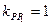
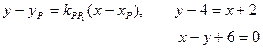
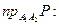
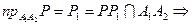
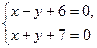
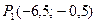
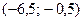
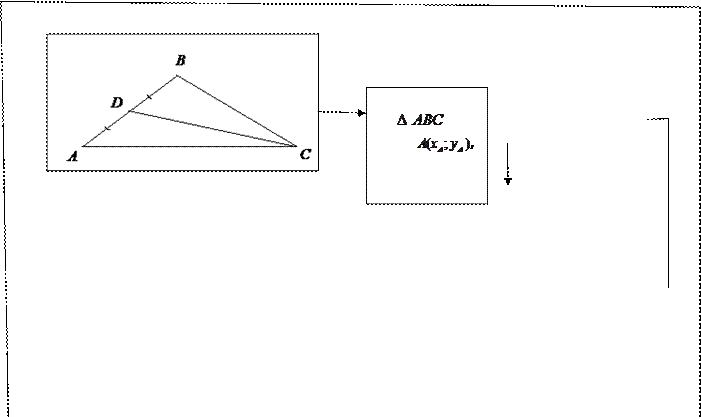
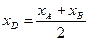 ,
, 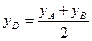


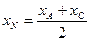 ,
,