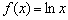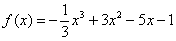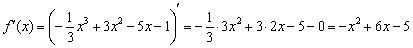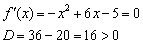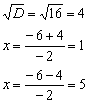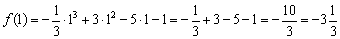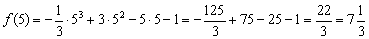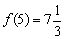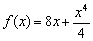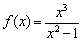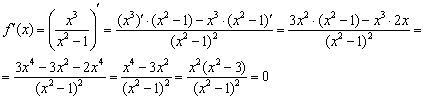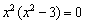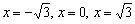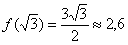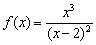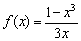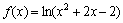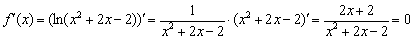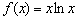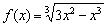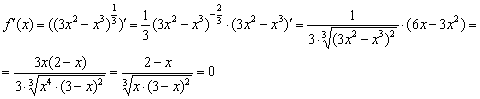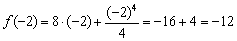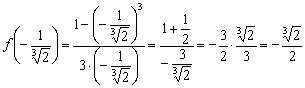Алгебра. Урок 5. Графики функций
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Парабола
Гипербола
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
0″ height=»346″ width=»346″ sizes=»(max-width: 346px) 100vw, 346px» data-srcset=»/wp-content/uploads/2017/01/Гипербола-1.png 346w,/wp-content/uploads/2017/01/Гипербола-1-150×150.png 150w,/wp-content/uploads/2017/01/Гипербола-1-300×300.png 300w,/wp-content/uploads/2017/01/Гипербола-1-176×176.png 176w,/wp-content/uploads/2017/01/Гипербола-1-60×60.png 60w, https://epmat.ru/wp-content/uploads/2017/01/Гипербола-1.png»>
Если k 0, ветви гиперболы проходят через II и IV четверти.
Квадратный корень
Функция y = x имеет следующий график:
Возрастающие/убывающие функции
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:
Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Возрастание и убывание функции
Вы будете перенаправлены на Автор24
При исследовании заданной функции особое внимание уделяется характеру ее поведения: возрастает, не возрастает, убывает, не убывает.
Примеры монотонных функций приведены на рисунках:
Рисунок 1. Возрастающая функция
Рисунок 2. Убывающая функция
Монотонные функции делят на:
Функция является возрастающей, если для большего значения аргумента соответствует большее значение заданной функции. Другими словами, если при возрастании значений аргумента значения заданной функции тоже возрастают, то заданная функция возрастает.
Функция является убывающей, если для большего значения аргумента соответствует меньшее значение заданной функции. Другими словами, если при возрастании значений аргумента значения заданной функции убывают, то заданная функция убывает.
Готовые работы на аналогичную тему
Функция является не возрастающей, если для большего значения аргумента соответствует большее или равное значение заданной функции.
Функция является не убывающей, если для большего значения аргумента соответствует меньшее или равное значение заданной функции.
Не возрастающая, не убывающая и постоянная функции не являются монотонными.
Монотонные функции обладают следующими свойствами:
Между монотонностью заданной функции и ее производной существует определенная связь, которая описывается следующими теоремами:
Сформулируем обратные теоремы.
Теорема, обратная к теореме 1.
Если заданная функция является возрастающей на некотором промежутке, то производная данной функции неотрицательна или не существует.
Теорема, обратная к теореме 2.
Если заданная функция является убывающей на некотором промежутке, то производная данной функции неположительная или не существует.
Для постоянной функции имеет место следующая теорема:
Алгоритм исследования функции на возрастание и убывание включает следующие этапы:
Следовательно, заданная функция убывает на всей области определения
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 16 02 2021
Убывающая функция: как распознать, примеры, упражнения
Содержание:
Хотя некоторые функции, подобные этой, характеризуются тем, что они уменьшаются по всей своей области, не все из них ведут себя так, есть те, которые увеличиваются, а также те, которые увеличиваются и уменьшаются в определенных интервалах домена. Изучение интервалов роста и уменьшения называется однообразие функции.
Точно так же можно рассматривать рост или уменьшение функции в определенной точке области. Но каждая функция, которая убывает в данном интервале, также убывает в каждой точке, которая ей принадлежит.
Как определить убывающую функцию?
График функции наглядно показывает, убывает она или нет. Если при движении в возрастающем смысле x функция «спускается», это означает, что она убывает.
И если у него есть интервалы, в которых он попеременно убывает и растет, что является наиболее обычным, так как они ясно показаны, наблюдая за поведением функции вдоль ее области определения, поскольку будут интервалы, в которых функция «поднимается» и другие, в которые он «спускается».
В качестве альтернативы, если график функции недоступен, аналитически можно определить, уменьшается ли он в точке или в интервале, по первой производной.
Критерий первой производной
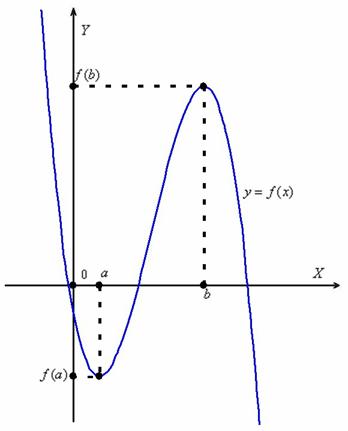
Обратите внимание на поведение убывающей функции, показанной на рисунке 2. Сегменты линии розового цвета касаются точек, координаты которых равны [а, е (а)] Y [а + ч, е (а + ч)] и имеют отрицательный наклон.
Для этой функции верно следующее:
Теорема для убывающих и возрастающих функций
Ранее упоминалось поведение функции в какой-то момент. Следующая теорема позволяет нам узнать интервалы, в которых функция убывает, увеличивается или становится постоянной:
-Если f´ (x) 0 для всех x, принадлежащих (a, b), говорят, что функция f (x) возрастает в (a, b).
-Наконец, если f´ (x) = 0 для всех x, принадлежащих интервалу (a, b), f (x) постоянна в указанном интервале.
Демонстрация
Функция 1 / x
Используя онлайн-программу построения графиков, такую как Geogebra, строят график функции f (x) = 1 / x, проверяя, что он убывает во всей области.
Аффинная функция
Решение
Первая производная от f (x) является непрерывной функцией, то есть не имеет точек разрыва, но обращается в нуль в:
Затем первая производная оценивается при произвольном значении x, принадлежащем каждому интервалу. Были выбраны следующие значения:
Для (- √3,0)
Для (0, √3)
Для (√3, ∞ +)
Ссылки
Исследование операций: для чего, модели, приложения
Возрастание, убывание и экстремумы функции
А сегодня в воздухе витает дух редкого единодушия, и я прямо чувствую, что все присутствующие горят желанием научиться исследовать функцию с помощью производной. Поэтому на экранах ваших мониторов незамедлительно появляется разумная добрая вечная терминология.
Зачем? Одна из причин самая что ни на есть практическая: чтобы было понятно, что от вас вообще требуется в той или иной задаче!
Монотонность функции. Точки экстремума и экстремумы функции
Рассмотрим некоторую функцию 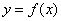
На всякий случай сразу избавимся от возможных иллюзий, особенно это касается тех читателей, кто недавно ознакомился с интервалами знакопостоянства функции. Сейчас нас НЕ ИНТЕРЕСУЕТ, как расположен график функции относительно оси 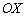
Функция возрастает на интервале, если для любых двух точек этого интервала, связанных отношением 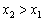
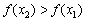
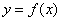
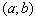
Аналогично, функция убывает на интервале, если для любых двух точек данного интервала, таких, что 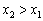
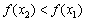
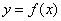
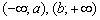
Если функция возрастает или убывает на интервале, то её называют строго монотонной на данном интервале. Что такое монотонность? Понимайте в буквальном смысле – однообразие.
Также можно определить неубывающую функцию (смягчённое условие 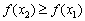
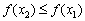
Теория рассматривает и другие подходы к определению возрастания/убывания функции, в том числе на полуинтервалах, отрезках, но чтобы не выливать на вашу голову масло-масло-масляное, договоримся оперировать открытыми интервалами с категоричными определениями – это чётче, и для решения многих практических задач вполне достаточно.
Таким образом, в моих статьях за формулировкой «монотонность функции» почти всегда будут скрываться интервалы строгой монотонности (строгого возрастания или строгого убывания функции).
Окрестность точки. Слова, после которых студенты разбегаются, кто куда может, и в ужасе прячутся по углам. …Хотя после поста Пределы по Коши уже, наверное, не прячутся, а лишь слегка вздрагивают =) Не беспокойтесь, сейчас не будет доказательств теорем математического анализа – окрестности мне потребовались, чтобы строже сформулировать определения точек экстремума. Вспоминаем:
Окрестностью точки называют интервал, который содержит данную точку, при этом для удобства интервал часто полагают симметричным. Например, точка 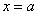
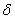

Собственно, определения:
Точка 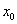
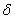
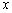
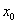
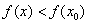
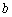
Точка 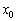
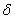
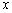
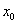
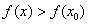
Примечание: требование симметричности окрестности вовсе не обязательно. Кроме того, важен сам факт существования окрестности (хоть малюсенькой, хоть микроскопической), удовлетворяющей указанным условиям
Точки 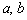
Как понимать слово «экстремум»? Да так же непосредственно, как и монотонность. Экстремальные точки американских горок.
Как и в случае с монотонностью, в теории имеют место и даже больше распространены нестрогие постулаты (под которые, естественно, подпадают рассмотренные строгие случаи!):
Точка 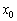
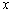
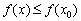
Точка 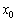
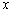
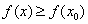
Заметьте, что согласно последним двум определениям, любая точка функции-константы (либо «ровного участка» какой-нибудь функции) считается как точкой максимума, так и точкой минимума! Функция 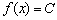
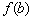
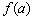
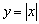
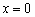
Да, кстати, о королевских особах:
– значение 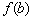
– значение 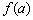
Общее название – экстремумы функции.
Пожалуйста, будьте аккуратны в словах!
Точки экстремума – это «иксовые» значения.
Экстремумы – «игрековые» значения.
! Примечание: иногда перечисленными терминами называют точки «икс-игрек», лежащие непосредственно на САМОМ ГРАФИКЕ функции.
Сколько может быть экстремумов у функции?
Ни одного, 1, 2, 3, … и т.д. до бесконечности. Например, у синуса бесконечно много минимумов и максимумов.
ВАЖНО! Термин «максимум функции» не тождественен термину «максимальное значение функции». Легко заметить, что значение 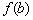
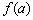
Чайникам на первых порах рекомендую создать и осмыслить небольшой терминологический конспект, чтобы не путать Иран с Ираком.
Подытожим наш небольшой экскурс в теорию контрольным выстрелом: что подразумевает задание «найдите промежутки монотонности и точки экстремума функции»?
Формулировка побуждает найти:
– интервалы возрастания/убывания функции (намного реже фигурирует неубывание, невозрастание);
– точки максимума и/или точки минимума (если таковые существуют). Ну и от незачёта подальше лучше найти сами минимумы/максимумы 😉
Как всё это определить? С помощью производной функции!
Как найти интервалы возрастания, убывания,
точки экстремума и экстремумы функции?
Многие правила, по сути, уже известны и понятны из урока о смысле производной.
Рассмотрим дифференцируемую на некотором интервале функцию 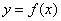
– если производная 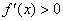
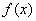
– если производная 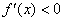
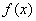
Примечание: справедливы и обратные утверждения.
Пусть точка 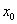
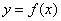
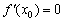
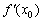
Но сначала потренируемся на кошках разделаемся с простейшими примерами. Почин положен в конце теоретической статьи о производной, и на очереди другие жертвы анализа. Заодно есть возможность провести маленькое самотестирование – насколько хорошо вы запомнили, как выглядят графики жизненно важных функций? В тяжелом случае, конечно же, следует открыть первый урок на соседней вкладке и щёлкать туда-сюда по мере комментариев.
Производная кубической функции 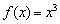
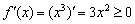
Действительно, кубическая парабола идёт «снизу вверх». Бесконечно близко около точки 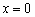
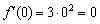
Функция 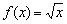
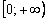
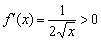
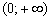
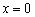
С геометрических позиций тут нет общей касательной. Однако в теории рассматриваются так называемые односторонние производные, и в указанной точке существует правосторонняя производная с правосторонней касательной. Желающие разобраться в этом подробнее могут покурить первый том матана.
Примечание: согласно информации первого параграфа, точка 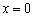
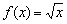
и слева и справа от данных точек. Так же не считаются точками экстремума крайние значения области определения арксинуса и арккосинуса (см. ниже).
Стандартная гипербола 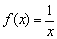
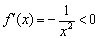
Здесь, к слову, точка 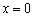
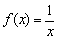
Экспоненциальная функция 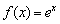
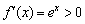
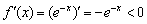
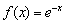
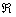
Что делает натуральный логарифм сегодня вечером?
Растёт:
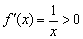
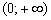
Начертите/распечатайте на соседних либо одном чертеже (иль просто представьте в уме) графики функции 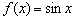
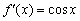
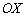
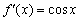
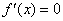
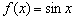
Аналогичная история с косинусом 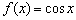
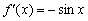
Производная тангенса 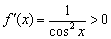
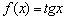
С котангенсом и его производной 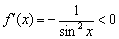
Арксинус на интервале 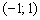
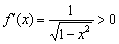
При 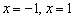
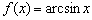
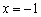
Думаю, вам не составит особого труда провести похожие рассуждения для арккосинуса и его производной.
Все перечисленные случаи, многие из которых представляют собой табличные производные, напоминаю, следуют непосредственно из определения производной.
Зачем исследовать функцию с помощью производной?
Чтобы лучше узнать, как выглядит график этой функции: где он идёт «снизу вверх», где «сверху вниз», где достигает минимумов максимумов (если вообще достигает). Не все функции такие простые – в большинстве случаев у нас вообще нет ни малейшего представления о графике той или иной функции.
Настала пора перейти к более содержательным примерам и рассмотреть алгоритм нахождения интервалов монотонности и экстремумов функции:
Найти интервалы возрастания/убывания и экстремумы функции
Решение:
1) На первом шаге нужно найти область определения функции, а также взять на заметку точки разрыва (если они существуют). В данном случае функция непрерывна на всей числовой прямой, и данное действие в известной степени формально. Но в ряде случаев здесь разгораются нешуточные страсти, поэтому отнесёмся к абзацу без пренебрежения.
2) Второй пункт алгоритма обусловлен
необходимым условием экстремума:
Если в точке 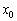
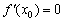
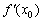
Смущает концовка? Экстремум функции «модуль икс».
Условие необходимо, но не достаточно, и обратное утверждение справедливо далеко не всегда. Так, из равенства 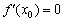
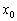
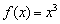
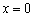
Но как бы там ни было, необходимое условие экстремума диктует надобность в отыскании подозрительных точек. Для этого следует найти производную и решить уравнение 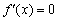
Получилось обычное квадратное уравнение:
Положительный дискриминант доставляет две критические точки:
Примечание: корни можно традиционно обозначить через 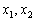
Итак, 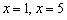
Но экстремумов в них может и не оказаться, поэтому нужно продолжить решение.
первое достаточное условие экстремума,
которое вкратце формулируется следующим образом: пусть функция дифференцируема в некоторой окрестности критической точки 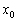
– если при переходе через точку 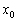
– если при переходе через точку 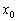
Тут всё очень и очень наглядно, представьте – функция росла-росла-росла, и после прохождения некоторого рубежа вдруг стала убывать. Максимум. Во втором случае график шёл-шёл-шёл «сверху вниз», а при переходе через точку 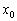
Исходя из вышесказанного, вытекает логичное решение: на числовой прямой нужно отложить точки разрыва функции, критические точки и определить знаки производной на интервалах, которые входят в область определения функции.
В рассматриваемом примере с непрерывностью на 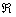
Напрашивается метод интервалов, который уже применялся для определения интервалов знакопостоянства функции. Так почему бы его не использовать для производной? Ведь производная тоже простая смертная функция, найдёшь её – и делай всё, что хочешь.
Внимание! Сейчас мы работаем с ПРОИЗВОДНОЙ, а не с самой функцией!
Перед нами парабола 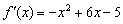

I) Берём какую-нибудь точку интервала 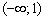
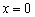
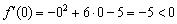
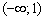
II) Выбираем точку 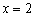
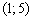
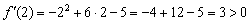
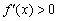
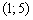
III) Вычислим значение производной в наиболее удобной точке 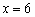
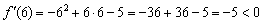
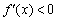
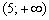
В результате получены следующие знаки производной:

Время собирать урожай!
На интервалах 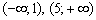
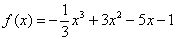
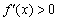
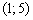
При переходе через точку 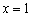
При переходе же через точку 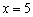
Ответ: функции возрастает на интервале 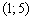
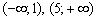
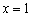
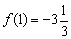
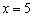
Остерегайтесь сокращенной записи 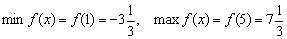
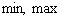
Пример так тщательно провёрнут через мясорубку, что грех не привести графическое изображение всех событий. Незнакомец теоретической части статьи снимает шляпу: 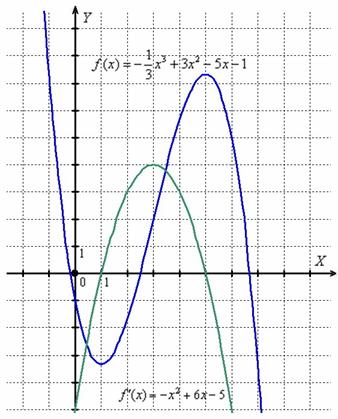
Что произошло? На первом этапе мы нашли производную 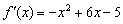
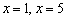
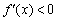
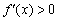
Помимо 1-го достаточного условия экстремума существует и 2-е достаточное условие, однако для исследования функций оно малоинформативно и больше используется в экстремальных задачах.
В начале первой статьи о графиках функции я рассказывал, как быстро построить параболу на примере 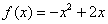
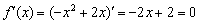
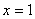
Найти промежутки монотонности и экстремумы функции
Это пример для самостоятельного решения. Полное решение и примерный чистовой образец оформления задачи в конце урока.
Наступил долгожданный момент встречи с дробно-рациональными функциями:
Исследовать функцию с помощью первой производной
Обратите внимание, как вариативно можно переформулировать фактически одно и то же задание.
Решение:
1) Функция терпит бесконечные разрывы в точках 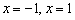
2) Детектируем критические точки. Найдём первую производную и приравняем её к нулю:
Решим уравнение 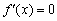
Таким образом, получаем три критические точки:
3) Откладываем на числовой прямой ВСЕ обнаруженные точки и методом интервалов определяем знаки ПРОИЗВОДНОЙ: 
Напоминаю, что необходимо взять какую-нибудь точку интервала, вычислить в ней значение производной 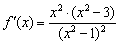
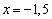
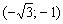
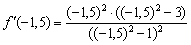
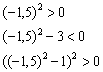
Два «плюса» и один «минус» дают «минус», поэтому 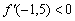
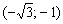
Действие, как вы понимаете, нужно провести для каждого из шести интервалов. Кстати, обратите внимание, что множитель числителя 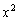
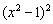
Итак, производная сообщила нам, что САМА ФУНКЦИЯ 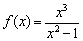
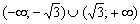
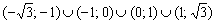
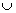
В точке 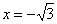
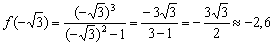
В точке 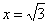
Подумайте, почему можно заново не пересчитывать второе значение 😉
При переходе через точку 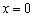
! Повторим важный момент: точки 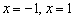
Ответ: функция возрастает на 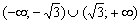
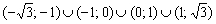
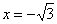
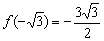
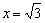
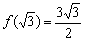
Знание интервалов монотонности и экстремумов вкупе с установленными асимптотами даёт уже очень хорошее представление о внешнем виде графика функции. Человек среднего уровня подготовки способен устно определить, что у графика функции 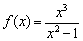
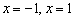
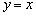
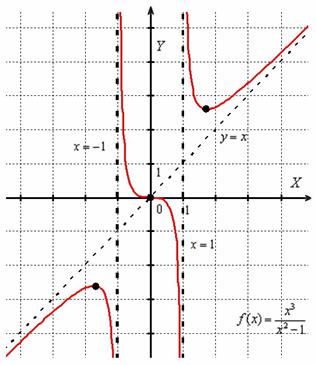
Постарайтесь ещё раз соотнести результаты исследования с графиком данной функции.
В критической точке 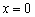
Найти экстремумы функции
Найти интервалы монотонности, максимумы и минимумы функции
…прямо какой-то Праздник «икса в кубе» сегодня получается.
Тааак, кто там на галёрке предложил за это выпить? =)
В каждой задаче есть свои содержательные нюансы и технические тонкости, которые закомментированы в конце урока.
Как отмечалось, в ходе выполнения задания всегда нужно внимательно следить за точками разрыва и интервалами, которые не входят в область определения функции. Казус состоит в том, что иногда производная может существовать на таких участках! Простейший пример: производная натурального логарифма 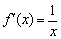
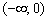
Типичный барьерный риф:
Найти интервалы монотонности и экстремумы функции
Приближаю оформление к боевым условиям и прекращаю нумерацию пунктов алгоритма.
Решение: в Примере 11 статьи об интервалах знакопостоянства была найдена область определения данной функции: 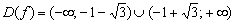
Вроде бы всё хорошо: у нас есть корень 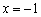
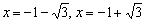
Но производная проявила своеволие – она в отличие от свого родителя определена и на интервале 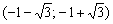
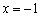

Функция убывает на интервале 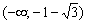
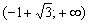
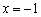
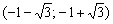
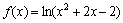
Ответ: функция убывает на интервале 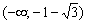
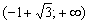
Будьте очень внимательны, если вам встретится логарифм или корень – в подобных примерах просто необходимо увАжить область определения функции!
Найти интервалы монотонности и экстремумы функции
Это приятный разгрузочный пример для самостоятельного решения.
И заключительный пример посвящен другому приключению непослушной дочери:
Найти точки экстремума функции
Решение: функция определена и непрерывна на всей числовой прямой.
Найдём критические точки:
На всякий случай детализирую преобразования знаменателя: 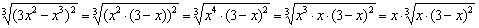
Таким образом, 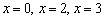
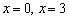
Определим знаки производной на полученных интервалах: 
Функция возрастает на интервале 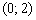
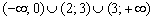
В точке 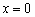
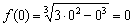
В точке 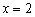
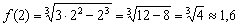
В точке 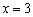
Ответ: 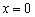
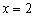
По условию требовалось найти точки экстремума и что-то добавлять излишне. Но в решении как бы невзначай вычислены и сами экстремумы 😉
Давайте посмотрим на на эту оригинальную картину: 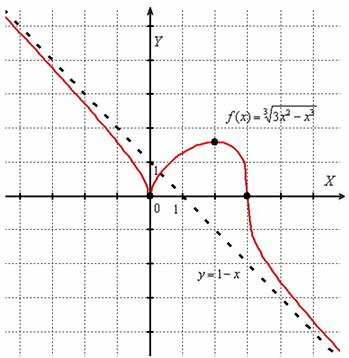
В точке 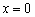
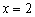
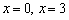
. да, родители и дети бывают разными. Но мама права в 95% случаев с погрешностью 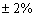
Пример 2: Решение:
1) Функция определена и непрерывна на всей числовой прямой.
2) Найдём критические точки: 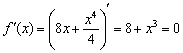
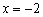
3) Методом интервалов определим знаки производной: 
Ответ: функция убывает на интервале 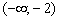
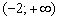
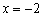
Пример 4: Решение:
1) Функция терпит бесконечный разрыв в точке 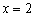
2) Найдём критические точки: 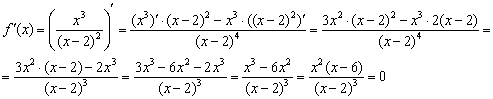
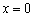
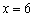
3) Методом интервалов определим знаки производной: 
В точке 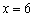
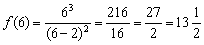
В точке 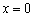
Ответ: в точке 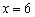
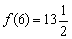
Примечание: обратите внимание, что информацию об интервалах монотонности раскрывать не обязательно, так как по условию требовалось найти только экстремумы функции
Пример 5: Решение:
1) Функция определена и непрерывна на всей числовой прямой кроме точки 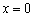
2) Найдём критические точки: 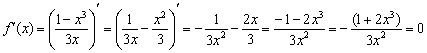
Примечание: в данном случае перед дифференцированием выгодно почленно разделить числитель на знаменатель
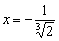
3) Определим знаки производной: 
Ответ: функция возрастает на 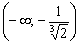
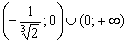
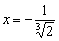
Пример 7: Решение:
Область определения: 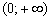
Найдём критические точки: 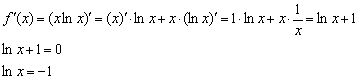
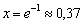
Определим знаки производной: 
Ответ: функция убывает на интервале 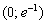
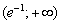
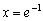
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5