Циклический алгоритм и его составление в информатике: примеры, решение
Содержание:
Алгоритм является классической совокупностью четко установленных норм для поиска решения задачи. Класс задач – произвольный. В структуру может входить последовательность действий, список инструментария, необходимый для поиска ответа на исходный вопрос задания.
Циклом называют некоторое повторение действия, вычисления.
Цикличный алгоритм, примеры которого можно встретить в повседневной жизни, описывает действия. Они повторяются до момента решения поставленной задачи. Иногда число повторений – обязательное условие задания. Информатика разделяет все структуры повторения на три вида:
Составление циклических алгоритмов – информатика и программирование
Главное правило составления конструктивов – конечность. Процесс должен осуществляться до определенного момента. Если окончание не наступает – структуру называют зацикленной. Состав структур с повторениями:
Часто встречается задание: приведите пример циклического алгоритма. Чтобы справиться с этой задачей, рекомендуется следовать принципам последовательности составления конструктивов:
Циклический алгоритм примеры – информатика
Сумма рассчитывается с помощью данной системы. Рассмотрим процесс на примере i-1nxiyi. Действуем по следующей схеме:
На уроке физики ученики должны использовать одинаковую формулу до того момента, пока выражение не станет верным. Без этого они не получат нужный результат.
§ 8.8. Программирование циклических алгоритмов. Цикл с условием
Содержание
Алгоритмическая конструкция цикл с условием
- цикл с предусловием (или типа while), цикл с постусловием и цикл с параметром (или цикл по переменной).
Инструкция while
Счетчики и накопители
Блок-схема 
Мы уже говорили, что в циклах часто используются операции постфиксного или префиксного инкремента или декремента. Эти операции могут сделать код более компактным. Например, две инструкции тела цикла в программе 8.8.2 можно заменить всего одной:
Аналогично программируется и накопление суммы. При этом, можно использовать изменяемое значение счетчика для каких-либо других целей, например, для нумерации вводимых чисел.
Задача 5. С клавиатуры вводится n целых чисел. Определить среднее арифметическое введенных чисел.
Вывод 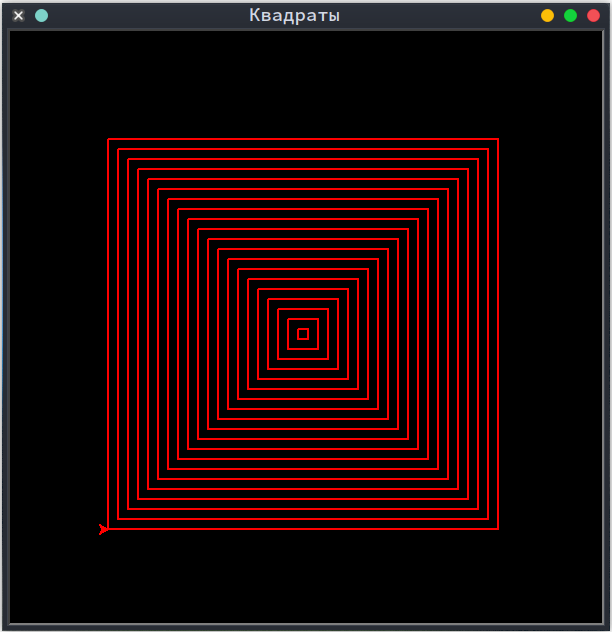
Параметры: n = 20, d = 10
Счетчик с произвольным шагом
В программах выше использовался счетчик с целочисленным шагом равным единице для определения количества шагов цикла. Но, в общем случае, счетчик может иметь произвольный шаг, в том числе дробный. Покажем это на примере.
Задача 7. Составить программу вывода таблицы значений квадратного корня чисел от 0.2 до 10.0 с шагом 0.2 и точностью до 4 знаков после запятой.
Возможно, программный код выглядит не очень изящно, но это неизбежная плата за табличное оформление вывода. Приведем пример с черепахой.
Задача 8. Составить программу в которой черепаха рисует параболу
Проход циклом по разрядам числа
Обсудим еще один тип задач в которых производится действия с разрядами числа. В этих задачах для работы с отдельными разрядами числа применяются операции целочисленного деления, которые мы изучили ранее. Поскольку количество разрядов в числе заранее неизвестно, то исходное число, на каждом шаге цикла, делится на 10 (с каждым шагом удаляется младший разряд), пока частное не станет равным нулю. Это значение является основанием прекратить деление и выйти из цикла.
Усовершенствуем программу 8.5.4 (задача 2) так, чтобы в итоге обрабатывалось число произвольной разрядности.
Инструкция do-while
Эту инструкцию цикла мы будем использовать в дальнейшем в тех задачах, где её применение будет более уместным, нежели другие инструкции циклов.
Блок-схема циклического алгоритма
Часто при решении задач приходится повторять выполнение операций по одним и тем же зависимостям при различных значениях входящих в них переменных и производить многократный проход по одним и тем же участкам алгоритма. Такие участки называются циклами. Алгоритмы, содержащие циклы, называется циклическими. Использование циклов существенно сокращает объем алгоритма.
Различают циклы с наперед известным и наперед неизвестным количеством проходов.
Пример 1. Рассмотрим пример алгоритма с циклом, имеющим наперед неизвестное количество проходов. Для этого решим следующую задачу. Указать наименьшее количество членов ряда натуральных чисел 1, 2, 3, …, сумма которых больше числа К.
Блок-схема алгоритма решения этой задачи приведена на рисунке 1. Она состоит из восьми блоков.
После начала работы в блоке 2 вводится значение числа К. Далее в блоке 3 переменная i получает значение 1, т. е. значение, с которого начнется отсчет натуральных чисел. Переменная S, предназначенная для накопления сумма этих чисел, перед началом суммирования получает значение 0. После этого управление передается блоку 5.
В нем при выполнении команды S = S + i производится сложение содержимого ячеек S и i, а результат записывается в ячейку S. Поскольку до операции сложения было S = 0, i = 1, то после операции будет S = 1. При записи нового значения старое содержимое ячейки S (нуль) стирается, а на его место записывается число 1.
Нужно обратить внимание на то, что если бы до этой операции в блоке 3 не была выполнена команда S = 0 (записать нуль в ячейку S ), то при нахождении суммы S + 1 возникла бы ошибка, поскольку из ячейки S была бы извлечена константа, которая оказалась там после распределения памяти.
После суммирования первого члена последовательности в блоке 6 выполняется проверка условия о превышении суммы S заданного числа К.
Если условие 6 не выполнится, то производится переход к блоку 4, где при выполнении операции значение переменной увеличивается на 1 и становится равным 2. Теперь алгоритм вновь вернется к блоку 5 и к старому значении суммы добавит новый член 2. После этого сумма станет равной 3. В блоке б вновь проверяется условие получения требуемой суммы и т. д. Цепочка блоков 5-4 будет обрабатываться вновь и вновь до того момента, когда однажды при определенном значении переменной i, наконец, выполнится условие S > К, т. е. когда накапливаемая в таком цикле сумма впервые превысит заданное значение К. Переменная i, значение которой при очередном проходе цепочки этих блоков увеличивается на 1, играет роль счетчика этого цикла.
Далее производится переход к блоку 7, где отпечатается значение количества членов ряда (извлечено и отпечатано число из ячейки i, которое там хранится в момент выполнения условия), суммы S и в блоке 8 алгоритм закончит работу.
Пример 2. Теперь приведем пример алгоритма, содержащего цикл с наперед известным количеством проходов (повторений). Алгоритм решает задачу накопления суммы положительных элементов одномерного массива Z длины N ( под длиной массива понимается количество его элементов ). Блок-схема алгоритма дана на рисунке 2.
Вначале в блоке 2 производится ввод двух переменных N и Z. Первая из них представляет одну ячейку. В нее записывается одна константа – число, равное количеству элементов массива Z. Именно такое количество ячеек объединяет другая переменная – Z.
Следует подчеркнуть, что если бы ввод этих переменных в блоке 2 производился в противоположном порядке, то это привело бы к ошибке. Действительно, невозможно заполнить N ячеек массива Z, когда самое N еще не известно (оно будет введено позже Z). Далее в блоке 3 переменной S присвоено начальное значение 0. Это сделано для того, чтобы приготовить ячейку к дальнейшему накоплению необходимой суммы.
Блоки 4-6 представляет собой сам цикл, в котором накапливается сумма.
Для того чтобы понять, как функционирует не только этот, а и любой другой цикл, обратимся к рисункам 3 и 4. На них показана общая структура цикла и его важнейшие параметры.
Как видно из рисунка 3, цикл состоит из заголовка и тела. Всякий цикл обязательно имеет свой счетчик.
На рисунке 4, где показана структура и параметры заголовка цикла, роль такого счетчика выполняет переменная i.
Внутри заголовка после счетчика и символа «=» через запятую указывает начальное и конечное значения счетчика и шаг его изменения (на рисунке 4 их роль выполняют переменные j, k, l соответственно). Если значение шага l = l, то его можно не указывать.
Сначала производится вход в цикл. После этого начинается его выполнение.
Внутри заголовка счетчику первоначально присваивается значение i = j. Затем выполняется блоки, образующие тело цикла. Обработка блоков внутри цикла производится по часовой стрелке. В результате после первого выполнения тела цикла управление вновь передается заголовку. Здесь к текущему значению счетчика добавится шаг. Теперь, если новое значение счетчика не вышло за свои пределы (т. е. не стало больше своего конечного значения при положительном шаге или меньше конечного значения – при отрицательном шаге), то снова выполняется тело цикла, вновь после возврата к заголовку к счетчику добавляется шаг. Так цикл будет выполняться до тех пор, пока значение счетчика однажды не выйдет за предписанный предел. Как только такой предел будет преодолен, произойдет выход из цикла и управление будет передано блоку, который следует сразу за циклом.
Вернемся к блок-схеме рис. 2. Заголовок ее цикла представлен блоком 4. Роль счетчика цикла играет переменная i, которая должна в цикле изменяться от 1 до N. Поскольку шаг явно не указан, то по умолчанию он подразумевается равным 1. Тело цикла образуют блоки 5 и 6.
Сразу после входа в цикл переменная i примет начальное значение i = 1. Далее в блоке 5 выполняется проверка положительности первого элемента массива Z (т. к. i = 1). Если этот элемент действительно положителен, то в блоке б он будет добавлен к переменной S, после чего выполняется возврат к заголовку цикла. Если этот элемент не положителен (т. е. нуль или отрицательный), то будет выполнен переход сразу к заголовку цикла, минуя блок суммирования 6.
На втором круге цикла счетчик i в заголовке увеличится на 1 и станет равным 2. Теперь, при новом выполнении тела цикла, в блоке 5 проверяется на положительность второй элемент массива Z и, если он положителен, то добавляется в сумму и т. д. Последний раз тело цикла выполнится при i = N. При этом значении счетчика проверяется последний элемент массива. Наконец, в заголовке цикла i примет значение N+1. Это значение выходит за предписанный предел, следовательно, произойдет выход из цикла и управление перейдет блоку 7. В этом блоке выводится накопленная сумма и алгоритм закончит работу.
Информатика
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
С повторяющимися действиями мы сталкиваемся и в обычной жизни и при решении задач. Проход стрелок часов каждую минуту, секунду, час, смена дня и ночи, ежедневные сборы в школу, еженедельная смена уроков, ежегодные поездки на море – примеров циклов повторения миллиарды. Несмотря на разнообразие происходящих процессов, большинство из них можно описать простыми конструкциями. Делая что-то раз за разом, мы не задумываемся, что ученые уже написали алгоритмы с повторением или циклы универсальными способами.
Циклы, их виды
Многие операции, действия выполняются однотипно много раз. Этот процесс повторения называют циклом, а повторяемая последовательность – телом цикла. Процедуру с повторяющимися этапами называют циклической.
Каждое повторение действий в алгоритмах – итерация.
Выделяют 3 основных вида повторяющихся структур:
Описывать подобные процессы удобно схематично или при помощи команд.
Цикл с предусловием
Описание цикла с условием двумя способами:
Особенность этой конструкции – существуют такие условия, когда команды не будут выполнены ни разу.
Циклический алгоритм, примеры:
алг забор
нц пока есть кирпичи и раствор цемента
если высота забора 1 алгоритм
Блок-схемы. Графическая реализация алгоритмов
Занятие 4. Графическая реализация циклического алгоритма
В рассмотрении циклического алгоритма следует выделить несколько понятий.
Тело цикла – это набор инструкций, предназначенный для многократного выполнения.
Итерация – это единичное выполнение тела цикла.
Переменная цикла – это величина, изменяющаяся на каждой итерации цикла.
Каждый цикл должен содержать следующие необходимые элементы:
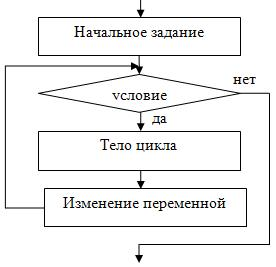
Циклы бывают двух видов – с предусловием и с постусловием. В цикле с предусловием сначала проверяется условие входа в цикл, а затем выполняется тело цикла, если условие верно. Цикл с предусловием представлен на рис. 2.9. Цикл с предусловием также может быть задан с помощью счетчика. Это удобно в тех случаях, когда точно известно количество итераций. В общем виде блок-схема, реализующая цикл с предусловием, представлена ниже. Сначала задается начальное значение переменной цикла, затем условие входа в цикл, тело цикла и изменение переменной цикла. Выход из цикла осуществляется в момент проверки условия входа в цикл, когда оно не выполняется, т.е. условие ложно. Цикл с предусловием может ни разу не выполниться, если при первой проверке условия входа в цикл оно оказывается ложным.
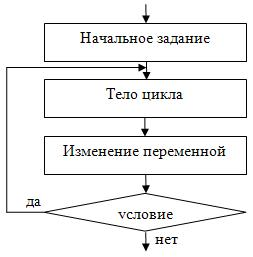
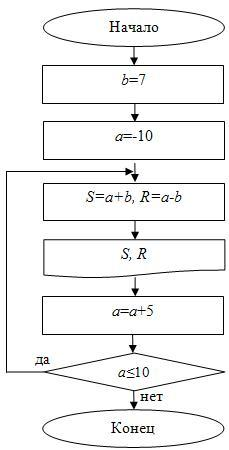
В цикле с постусловием сначала выполняется тело цикла, а потом проверяется условие. Циклический алгоритм с постусловием представлен на рис. 2.10.
Если условие верно, то итерация повторяется, если же неверно, то осуществляется выход из цикла. В отличие от цикла с предусловием, любой цикл с постусловием всегда выполнится хоть раз.
Примечание. Как видно из представленных блок-схем для циклов с предусловием и постусловием, условие записывается внутри блока условия (формы ромба), как и в разветвляющемся алгоритме. Принципиальная разница между разветвляющимся и циклическим алгоритмами при графической реализации состоит в том, что в циклическом алгоритме в обязательном порядке присутствует стрелка, идущая наверх. Именно эта стрелка обеспечивает многократный повтор тела цикла.
Приведем простейшие примеры, соответствующие циклическому алгоритму.
Пример 7. Вася звонит Пете, но у Пети может быть занята линия. Составить блок-схему действий Васи в этом случае.
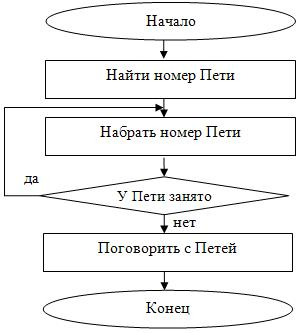
Решение. Когда телефонная линия занята, то необходимо снова и снова набирать номер, пока Петя не закончит предыдущий разговор, и телефонная линия не окажется вновь свободной. Блок-схема представлена на рис. 2.11.
Здесь тело цикла состоит из одного действия «Набрать номер Пети», т.к. именно это действие следует повторять, пока линия будет занята. Под итерацией цикла понимается очередная попытка дозвониться до Пети. Как таковой переменной цикла здесь нет, т.к. ситуация взята из жизни. Выход из цикла происходит в тот момент, когда условие «У Пети занято» стало неверным, т.е. телефонная линия свободна – действительно, нет необходимости больше набирать номер Пети. В данном примере применен цикл с постусловием, т.к. сначала необходимо набрать номер Пети, ведь иначе мы не можем ответить на вопрос – занята ли линия у Пети.
Пример 8. Ученику требуется купить учебник. Составить блок-схему, описывающую действия ученика в случае, если учебника нет в ряде магазинов.
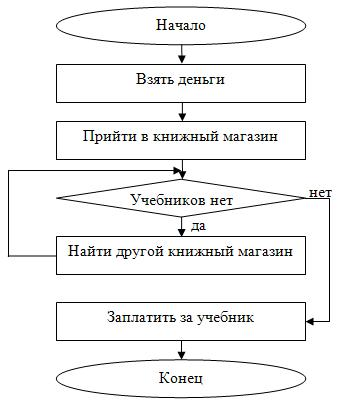
Решение. Действия ученика в данном примере очевидны: когда он приходит в первый и любой последующий магазины, то возможны два варианта – учебник имеется в наличии или учебника нет в продаже. Если учебника нет в продаже, то ученику следует пойти в другой книжный магазин и спросить данный учебник, и т.д. пока учебник не будет куплен, т.к. перед учеником стоит конечная цель – купить учебник. Мы будем использовать цикл с предусловием, т.к. сначала требуется найти магазин, имеющий в наличии данный учебник. Цикл будет выполняться, пока условие «В данном магазине нет учебника» будет верным, а выход из цикла осуществится, когда условие станет ложным, т.е. когда ученик придет в магазин, в котором есть данный учебник. Действительно, в этом случае ученик купит нужный ему учебник и не будет больше искать книжные магазины. Результат блок-схемы представлен на рис. 2.12.
Здесь тело цикла состоит из одного действия «Найти другой книжный магазин». Переменной цикла в явном виде нет, но можно подразумевать номер магазина, в который пришел ученик в очередной раз. Как любой другой цикл с предусловием, данный цикл может ни разу не выполниться (не иметь итераций), если в первом же магазине окажется нужный учебник.
Примечание. Если в данную задачу добавить условие выбора учебника в жесткой или мягкой обложке, как в примере 5, то оно появится после выхода из цикла. На реализацию циклического алгоритма данное условие не повлияет.
Тело цикла состоит из нескольких действий: вычисление суммы, вычисление разности и вывод полученных данных на экран. Таким образом, у нас получится несколько значений сумм и разностей, т.к. 

Данная задача может быть сделана и с циклом с предусловием, и с постусловием. В этом случае тело цикла, условие и изменение переменной цикла будут такими же, как и в цикле с предусловием, но сначала необходимо выполнить тело цикла, а потом проверить условие для выполнения следующей итерации.
Приведем блок-схему, использующую цикл с постусловием, на рис. 2.14.
В данной задаче также могут быть соединены циклический и разветвляющийся алгоритмы, если по условию задачи требуется сравнить полученные значения суммы и разности, как в примере 6. В этом случае цикл можно реализовать как с предусловием, так и с постусловием, а сравнение суммы и разности добавится внутрь тела цикла, т.к. следует сравнить между собой все полученные суммы и разности. Организация самого цикла останется прежней. Приведем на рис. 2.15а блок-схему с предусловием, а на рис. 2.15б блок-схему с постусловием.