Слово Как пишется значок перпендикулярности - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Перпендикулярные прямые — основные свойства, признаки и правила построения

В геометрии распространено понятие прямых. Они обозначаются двумя большими латинскими буквами или одной маленькой. При построении линии могут пересекаться и иметь только одну общую точку. Взаимно перпендикулярные прямые находятся относительно друг друга под углом 90°. Построение проводится при применении специальных инструментов.

Основные свойства

При рассмотрении того, какие прямые называют перпендикулярными, нужно уделить внимание свойствам. Они выглядят следующим образом:

Для обозначения перпендикуляра применяется знак «⊥». В подобном случае угол составляет 90°. На чертеже пересечение обозначается своеобразным квадратом, которые рисуется от двух пересекающихся линий.

Доказательство взаимного расположения

Рассматриваемый термин получил широкое распространение, он фигурирует практически в каждой геометрической задаче. В некоторых случаях о взаимном расположении известно, в других это нужно доказать. Задача доказательства заключается в определении прямого угла между двумя прямыми или плоскостями. Необходимое и достаточное условие перпендикулярности заключается в теореме:

Для определения расположения плоскостей или отрезков относительно друг друга следует провести геометрическое построение. Проходить отрезки должны в одной точке.

Определение перпендикулярности прямой и плоскости

Рассматривая определение перпендикулярных прямых следует учитывать, что подобное свойство применимо к плоскости. Основной признак заключается в перпендикулярности отрезка к любому другому, который находится в плоскости. Перпендикулярность прямых в пространстве указывается определенным знаком.

Доказать перпендикулярность можно проведя геометрические построения. Признаки расположения плоскости и прямой под углом 90° заключаются в следующем:

Отрезки могут быть также параллельными. В этом случае нет точки, в которой будут они пересекаться.

Построение перпендикуляра

Выдержать угловой коэффициент можно различным образом. В большинстве случаев для этого нужно иметь при себе циркуль. Построить перпендикуляр можно следующим образом:

Существенно упростить задачу можно путем применения специального чертежного инструмента, к примеру, любого прямоугольного треугольника. Он может называться угольником, основной его признак заключается в наличии двух перпендикулярных плоскостей. Построение проводится следующим образом:

В геометрии чаще всего применяется именно второй способ. Однако первый урок позволяет начертить два взаимно перпендикулярных отрезка с высокой точностью. Недостаток применения циркуля заключается в наличии вспомогательных линий, которые стереть сложно. Написать о взаимном расположении линий можно в описательной записке.

Трехмерное пространство

В начертательной геометрии линии всегда находятся в двухмерном пространстве. В специальных программах можно начертить отрезки в трехмерном пространстве. Подобное взаимное расположение может выглядеть следующим образом:

В жизни подобное расположение прямых встречается крайне часто. Проверить угол можно при применении специальных инструментов.

Четырехмерная система координат и лемма

Некоторые программы работают с четырехмерным пространством. Взаимное расположение плоскостей под прямым углом в этом случае имеет два смысла: они могут быть перпендикулярны в трехмерном смысле при образовании двугранного угла 90°.

Рассматриваться взаимное расположение плоскостей может и в 4-мерном смысле. Условия выглядят следующим образом:

Условия четырехмерного пространства определяют то, что через одну точку можно провести 6 взаимно перпендикулярных плоскостей. Определять их взаимное расположение можно несколькими различными способами.

Лемма, касающаяся перпендикулярности, связана с определением параллельности. Если одна из параллельных линий расположена под прямым углом относительно плоскости или отрезка, то вторая также перпендикулярна. Ответ на многие задачи связан с доказательством леммы:

При соблюдении условий полученный угол будет являться прямым. С учетом проведенных построений можно сформулировать определение перпендикулярности параллельных отрезков.

Применение термина

Как ранее было отмечено, встречается большое количество примеров применения рассматриваемого термина. На основе теоремы и доказательства были созданы различные формулы, позволяющие определить протяженность одного из сторон геометрической фигуры.

В средних и старших классах встречается большое количество задач, связанных с определением угла и протяженности сторон построенной фигуры. В некоторых случаях проводится построение диагонали, которая делит 90° на две равные части.

В жизни взаимное перпендикулярное расположение плоскостей встречается крайне часто. Примером служат несущие элементы различных сооружений. Подобное расположение позволяет правильно распределить оказываемую нагрузку. Править наклон можно путем применения специальных измерительных инструментов.

Многие геометрические фигуры построены на основе перпендикулярного расположения отрезков. Наиболее распространен параллелограмм или квадрат, треугольник. За счет выдерживания правильного угла обеспечивается также взаимное параллельное расположение сторон.

Приведенная выше информация указывает на то, что определение угла, под которым расположены плоскости, проводится в самых различных сферах. Инженеры и строители должны с высокой точностью контролировать этот показатель.

Источник

Как пишется значок перпендикулярности

Углы бывают острые, прямые и тупые.

Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.

Два угла с одной общей стороной называются смежными.

На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.

Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°

При пересечении двух прямых образуются четыре угла:

Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.

∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4

То же справедливо и для ∡1 и ∡3.

Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.

Перпендикулярность прямых принято обозначать так: a⟂b

Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!

Теорема о перпендикулярных прямых

Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.

Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.

Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.

Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.

Свойство перпендикулярных прямых

Две прямые, перпендикулярные третьей, не пересекаются.

Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.

У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Попробовать бесплатно

Интересное по рубрике

Найдите необходимую статью по тегам

Подпишитесь на нашу рассылку

Мы в инстаграм

Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Посмотреть

Рекомендуем прочитать

Реальный опыт семейного обучения

Звонок по России бесплатный

Посмотреть на карте

Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.

Источник

Перпендикулярность

Содержание

На плоскости

Перпендикулярные прямые

Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.

В аналитическом выражении прямые, заданные линейными функциями и будут перпендикулярны, если выполнено условие . Эти же прямые будут перпендикулярны, если . (Здесь — углы наклона прямой к горизонтали)

Для обозначения перпендикулярности имеется общепринятый символ: , предложенный в 1634 году французским математиком Пьером Эригоном.

Построение перпендикуляра

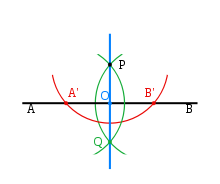
Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А’ и В’.

Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A’ и В’ соответственно, проходящими через точку Р. Кроме точки Р есть ещё одна точка пересечения этих полуокружностей, назовём её Q.

Шаг 3: (синий) Соединяем точки Р и Q. PQ и есть перпендикуляр к прямой АВ.

Координаты точки основания перпендикуляра к прямой

A(xa,ya) и B(xb,yb) — прямая, O(xo,yo) — основание перпендикуляра, опущенного из точки P(xp,yp).

Если xa = xb (вертикаль), то xo = xa и yo = yp. Если ya = yb (горизонталь), то xo = xp и yo = ya.

Во всех остальных случаях

xo = (xa*(yb-ya)^2 + xp*(xb-xa)^2 + (xb-xa) * (yb-ya) * (yp-ya)) / ((yb-ya)^2+(xb-xa)^2); yo = (yb-ya)*(xo-xa)/(xb-xa)+ya.

В трёхмерном пространстве

Перпендикулярные прямые

Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим прямым, лежащим в одной плоскости и перпендикулярным в ней.

Перпендикулярность прямой и плоскости

Определение: Прямая называется перпендикулярной плоскости, если она перпендикулярна всем прямым лежащим в этой плоскости.

Признак: Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Перпендикулярные плоскости

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.

В многомерных пространствах

Перпендикулярность плоскостей в 4-мерном пространстве

Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.

Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.

В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).

Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно : xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).

Перпендикулярность прямой и гиперплоскости

Пусть задано n-мерное евклидово пространство (n>2) и ассоциированное с ним векторное пространство , а прямая l с направляющим векторным пространством и гиперплоскость с направляющим векторным пространством (где , ) принадлежат пространству .

Прямая l называется перпендикулярной гиперплоскости , если подпространство ортогонально подпространству , то есть

Источник

Как пишется значок перпендикулярности

Допуск пересечения осей

Суммарные допуски формы и расположения

Допуск радиального биения

Допуск торцового биения

Допуск биения в заданном направлении

Допуск полного радиального биения

Допуск полного торцового биения

Допуск формы заданного профиля

Допуск формы заданной поверхности

Формы и размеры знаков приведены в приложении 1.

Примеры указания на чертежах допусков формы и расположения поверхностей приведены в приложении 2.

Примечание. Суммарные допуски формы и расположения поверхностей, для которых не установлены отдельные графические знаки, обозначают знаками составных допусков в следующей последовательности: знак допуска расположения, знак допуска формы.

— знак суммарного допуска параллельности и плоскостности;

— знак суммарного допуска перпендикулярности и плоскостности;

— знак суммарного допуска наклона и плоскостности.

1.2. Допуск формы и расположения поверхностей допускается указывать текстом в технических требованиях, как правило, в том случае, если отсутствует знак вида допуска.

1.3. При указании допуска формы и расположения поверхностей в технических требованиях текст должен содержать:

указание поверхности или другого элемента, для которого задается допуск (для этого используют буквенное обозначение или конструктивное наименование, определяющее поверхность);

числовое значение допуска в миллиметрах;

указание баз, относительно которых задается допуск (для допусков расположения и суммарных допусков формы и расположения);

указание о зависимых допусках формы или расположения (в соответствующих случаях).

1.4. При необходимости нормирования допусков формы и расположения, не указанных на чертеже числовыми значениями и не ограничиваемых другими указанными в чертеже допусками формы и расположения, в технических требованиях чертежа должна быть приведена общая запись о неуказанных допусках формы и расположения со ссылкой на ГОСТ 25069-81* или другие документы, устанавливающие неуказанные допуски формы и расположения.

* С 1 января 2004 г. введен в действие ГОСТ 30893.2-2002 (здесь и далее).

(Введен дополнительно, Изм. N 1).

2. НАНЕСЕНИЕ ОБОЗНАЧЕНИЙ ДОПУСКОВ

2.1. При условном обозначении данные о допусках формы и расположения поверхностей указывают в прямоугольной рамке, разделенной на две и более части (черт.1, 2), в которых помещают:

2.2. Рамки следует выполнять сплошными тонкими линиями. Высота цифр, букв и знаков, вписываемых в рамки, должна быть равна размеру шрифта размерных чисел.

Графическое изображение рамки приведено в приложении 1.

2.3. Рамку располагают горизонтально. В необходимых случаях допускается вертикальное расположение рамки.

Не допускается пересекать рамку какими-либо линиями.

2.4. Рамку соединяют с элементом, к которому относится допуск, сплошной тонкой линией, заканчивающейся стрелкой (черт.3).

Соединительная линия может быть прямой или ломаной, но направление отрезка соединительной линии, заканчивающегося стрелкой, должно соответствовать направлению измерения отклонения. Соединительную линию отводят от рамки, как показано на черт.4.

В необходимых случаях допускается:

проводить соединительную линию от второй (последней) части рамки (черт.5а);

заканчивать соединительную линию стрелкой и со стороны материала детали (черт.5б).

2.5. Если допуск относится к поверхности или ее профилю, то рамку соединяют с контурной линией поверхности или ее продолжением, при этом соединительная линия не должна быть продолжением размерной линии (черт.6, 7).

2.6. Если допуск относится к оси или плоскости симметрии, то соединительная линия должна быть продолжением размерной линии (черт.8а, б). При недостатке места стрелку размерной линии допускается совмещать со стрелкой соединительной линии (черт.8в).

Если размер элемента уже указан один раз, то на других размерных линиях данного элемента, используемых для условного обозначения допуска формы и расположения, его не указывают. Размерную линию без размера следует рассматривать как составную часть условного обозначения допуска формы или расположения (черт.9).

2.7. Если допуск относится к боковым сторонам резьбы, то рамку соединяют с изображением в соответствии с черт.10а.

Если допуск относится к оси резьбы, то рамку соединяют с изображением в соответствии с черт.10б.

Источник