Слово Как пишется интервал в математике - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Открытый числовой луч

Открытый луч – интервал с бесконечно большим числом точек. При объяснении понятие «числовой» часто опускается, при этом смысл не меняется.

Точки расположены по одну сторону от определенной переменной, признанной началом координат.

Находиться они могут как с правой, так и с левой стороны. При этом если за основу берется А, то множество обозначается следующим образом:

Таким образом указываются координаты. Читается как «от минус бесконечности до А» и «от А до плюс бесконечности».

Также можно охарактеризовать неравенством:

Знак зависит от расположения луча относительно А.

Замкнутый числовой луч

Замкнутый луч отличается от открытого тем, что к множеству относится А.

Также ему соответствует условие:

х ≤ А (значение меньше или равно А) или (-∞; А], то есть используются квадратные скобки;

х ≥ А (значение больше или равно А) или [А; +∞).

При графическом изображении А в этом случае закрашивается, на рисунке она черная.

Что касается открытого луча, то там А остается пустой, еще ее называют выколотой. Она связана с переменной строгим неравенством, не принадлежит к рассматриваемому множеству.

Числовой отрезок

Отрезок – замкнутый, закрытый промежуток или расстояние. Это множество переменных, расположенных на прямой между двумя точками, А и В. При этом они относятся к рассматриваемому множеству и называются концами.

При изображении они будут закрашены. Остальные точки отрезка считаются внутренними.

Интервал

Интервал представляет собой открытый отрезок, от которого он отличается тем, что границы к нему не относятся. Интервалу принадлежат исключительно внутренние точки прямой, границы же будут выколоты.

Источник

Поиск ответа

Слово «век» в научной литературе, как хорошо известно, сокращается и пишут «в.», а во множественном числе «вв.» Однако теперь при указании временного интервал а часто пишут в единственном числе: «XIX-XX в.» Правильно ли это? Не следует ли писать «XIX-XX вв.»? От чего это зависит? Спасибо!

Ответ справочной службы русского языка

Сокращение в. при указании на несколько веков неправильно, в этих случаях нужно использовать только сокращение вв.

Ответ справочной службы русского языка

Не рекомендуется применять тире в качестве знака интервал а значений, когда одно из значений величины положительное, а другое – отрицательное или когда оба значения отрицательные. Интервал в этом случае лучше обозначать многоточием: –4,0. +0,2 °С (лучше начать с отрицательного значения).

Как правильно писать «по не ответу» или «по неответу»? Пример предложения: «При установке переадресации «по неответу» можно установить интервал времени».

Ответ справочной службы русского языка

Какой символ между днями недели вставлять грамотно: Понедельник — пятница или Понедельник-пятница, или как-то еще?

Ответ справочной службы русского языка

Образцы из нефтенасыщенного и не*люминесцирующего интервал ов. Слитно или раздельно пишется не- с причастием?

Ответ справочной службы русского языка

Правильно ли я понимаю, что при указании интервал а в порядковых числительных всегда используется тире, а не дефис? То есть нормативным считается написание
«ученики 1—2-х классов»? И неверным будет написание «ученики 1-2-х классов»?

Ответ справочной службы русского языка

Добрый день!
Подскажите, пожалуйста, корректный вариант: «с интервал ом в 30 минут» ЛИБО «с интервал ом 30 минут».
Обновление списков выполняется сервером автоматически с интервал ом в 30 минут.
Благодарю!

Ответ справочной службы русского языка

Корректно: с интервал ом 30 минут (ср. с аналогичными конструкциями без предлога «в»: тиражом 5 тысяч экземпляров, глубиной 20 метров и т. п.) Но при этом: раз в тридцать минут, раз в час и т. п.

Здравствуйте! Как правильно: референТное (значение, интервал ) или референСное?

Ответ справочной службы русского языка

Подскажите, пожалуйста, в случае «полгода-год» между этими словами должно стоять тире с пробелами или без? Я знаю что при числах «два-три» пробелы не нужны. А как в этом случае?

Ответ справочной службы русского языка

При обозначении примерного интервал а (как в Вашем случае) используется дефис без пробелов.

Ответ справочной службы русского языка

А разве сочетание «временной интервал » не подходит?

В октябре-ноябре 1998 года он находился далеко от города. В октябре-ноябре правильно писать через дефис или через тире?

Ответ справочной службы русского языка

Написание зависит от значения. Если сочетание имеет значение приблизительного указания (то ли в октябре, то ли в ноябре), ставится дефис: в октябре-ноябре. Если же сочетание обозначает интервал значений («от. до»), ставится тире: в октябре – ноябре (т. е. с начала октября по конец ноября).

Ответ справочной службы русского языка

В справочнике Д. Э. Розенталя речь идет о правилах постановки тире. О том, надо или не надо отбивать тире от цифр пробелами, здесь ничего не сказано (это справочник по правописанию, а не по техническому оформлению текстов). Поэтому ориентироваться в этом вопросе на справочник Д. Э. Розенталя вряд ли целесообразно: конкретной рекомендации нет, а наличие пробелов в примерах вполне может быть ошибкой верстки. А вот в «Справочнике издателя и автора» А. Э. Мильчина, Л. К. Чельцовой (эта книга посвящена как раз вопросам редакционно-издательского оформления изданий) дано прямое указание: тире, по техническим правилам набора, не должно отбиваться от цифр.

В чём разница употребления среднего (–) и длинного (—) тире?
Слышала, что длинное тире используется лишь в СМИ и книгах, так ли это?
И какой знак лучше использовать в дипломных работах?
Спасибо!

Ответ справочной службы русского языка

Как правильно записывать слово век или века в след. выражении временного интервал а:

Ответ справочной службы русского языка

Первые два варианта вполне возможны.

Многие его стихотво­рения этого периода (1560–1562) содержат философские и политические мотивы.

Ответ справочной службы русского языка

Используется тире без пробелов.

Источник

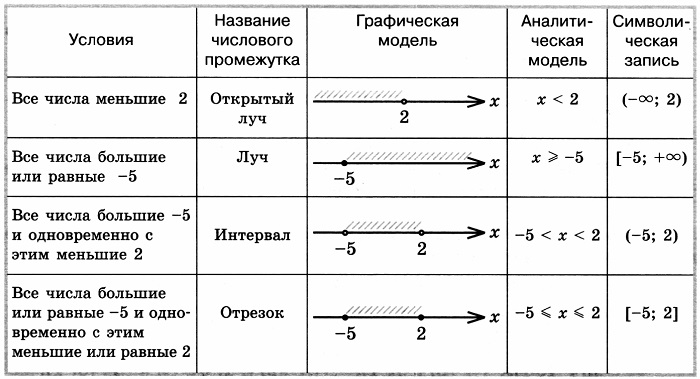
Числовые промежутки. Контекст. Определение

Введём понятие числового промежутка. Среди числовых множеств, то есть множеств, объектами которых являются числа, выделяют так называемые числовые промежутки. Их ценность в том, что очень легко вообразить множество, соответствующее указанному числовому промежутку, и наоборот. Поэтому с их помощью удобно записывать множество решений неравенства. Тогда как множеством решения уравнения будет не числовой промежуток, а просто несколько чисел на числовой прямой, с неравенствами, иначе говоря, любыми ограничениями значения переменной появляются числовые промежутки.

— это множество всех точек числовой прямой, ограниченное данным числом или числами (точками на числовой прямой).

Числовой промежуток любого вида (множество значений x, заключённых между некоторыми числами) всегда можно представить тремя видами математических обозначений: специальными обозначениями промежутков, цепочками неравенств (одним неравенством или двойным неравенством) или геометрически на числовой прямой. По сути, все эти обозначения имеют один смысл. Они дают ограничение(-я) для значений какого-то математического объекта, переменной величины (некоторой переменной, любого выражения с переменной, функции и т.д.).

Из вышесказанного можно понять, что так как можно по-разному ограничить область числовой прямой (есть разные типы неравенств), то и типы числовых промежутков бывают разные.

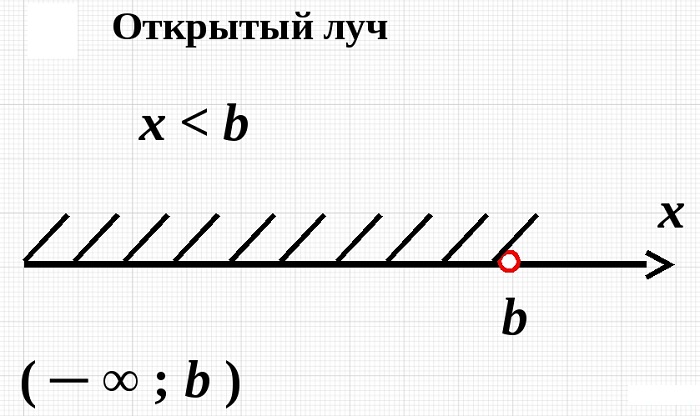
Виды числовых промежутков

Каждый тип числового промежутка имеет собственное название, особое обозначение. Для обозначения числовых промежутков используют круглую и квадратную скобку. Круглая скобка означает, что конечная, определяющая границу, точка на числовой прямой (конец) у этой скобки не входит во множество точек данного промежутка. Квадратная скобка означает, что конец входит в промежуток. С бесконечностью (с этой стороны промежуток не ограничен) используют круглую скобку. Иногда вместо круглых скобок можно писать квадратные, повёрнутые в обратную сторону: (a;b) ⇔]a;b[

С помощью промежутков в математике обозначается очень большое количество вещей: есть промежутки изоляции при решении уравнений, промежутки интегрирования, промежутки сходимости рядов. Промежутками принято всегда обозначать при при исследовании функции её область значений и область определения. Промежутки очень важны, например, есть теорема Больцано — Коши (можно узнать больше в «Википедии»).

Системы и совокупности неравенств

Система неравенств

Любую систему можно решать графически с использованием числовой прямой. Там, где решения составляющих систему неравенств пересекаются и будет решение самой системы.

Представим для каждого случая графическое решение.

Далее, системы неравенств можно классифицировать как равносильные, если они имеют общее множество решений. Отсюда (как можно видеть выше) следует, что более сложные системы можно упрощать (например, используя геометрическое решение).

Фигурную скобку можно условно, грубо говоря, назвать эквивалентом союза «И» для неравенств

Совокупность неравенств

Итак, все неравенства в совокупности объединяют скобкой совокупности «[«. Если значение переменной удовлетворяет хотя бы одному неравенству из совокупности, то оно принадлежит множеству решений всей совокупности. Также и с уравнениями (опять же их можно назвать частным случаем).

Источник

Реальные интервалы играют важную роль в теории интеграция, потому что они являются простейшими наборами, чей «размер» (или «меру», или «длину») легко определить. Затем понятие меры может быть расширено на более сложные наборы действительных чисел, что приведет к Мера Бореля и в конечном итоге Мера Лебега.

Интервалы имеют ключевое значение для интервальная арифметика, генерал числовые вычисления метод, который автоматически обеспечивает гарантированные вложения для произвольных формул, даже при наличии неопределенностей, математических приближений и арифметическое округление.

Аналогичным образом определяются интервалы на произвольной полностью заказанный набор, например целые числа или рациональное число. Обозначение целочисленных интервалов рассматривается в специальном разделе ниже.

Содержание

Терминология

Интервал называется левый закрытый если в нем есть минимальный элемент, закрыто вправо если есть максимум, и просто закрыто если есть и то, и другое. Эти определения обычно расширяются, чтобы включить пустое множество и неограниченные интервалы (слева или справа), так что закрытые интервалы совпадают с закрытые наборы в этой топологии.

Примечание о противоречивой терминологии

Условия сегмент и интервал были использованы в литературе двумя по существу противоположными способами, что привело к двусмысленности при использовании этих терминов. В Энциклопедия математики [4] определяет интервал (без квалификатора), чтобы исключить обе конечные точки (т. е. открытый интервал) и сегмент чтобы включить обе конечные точки (т.е. замкнутый интервал), в то время как Рудина Принципы математического анализа [5] вызывает наборы формы [а, б] интервалы и множества вида (а, б) сегменты на протяжении. Эти термины, как правило, встречаются в более старых работах; современные тексты все больше отдают предпочтение этому термину интервал (квалифицировано открыто, закрыто, или полуоткрытый), независимо от того, включены ли конечные точки.

Обозначения интервалов

Включение или исключение конечных точек

Чтобы указать, что одна из конечных точек должна быть исключена из набора, соответствующую квадратную скобку можно либо заменить скобкой, либо перевернуть. Оба обозначения описаны в Международный стандарт ISO 31-11. Таким образом, в обозначение конструктора наборов,

Оба обозначения могут пересекаться с другими случаями использования круглых и квадратных скобок в математике. Например, обозначение (а, б) часто используется для обозначения упорядоченная пара в теории множеств координаты из точка или вектор в аналитическая геометрия и линейная алгебра, или (иногда) комплексное число в алгебра. Поэтому Бурбаки ввел обозначения ]а, б[ для обозначения открытого интервала. [6] Обозначение [а, б] тоже иногда используется для заказанных пар, особенно в Информатика.

Бесконечные конечные точки

Целочисленные интервалы

Классификация интервалов

Свойства интервалов

Интервалы в точности соответствуют связанный подмножества р < Displaystyle mathbb > . Отсюда следует, что изображение интервала любым непрерывная функция это тоже интервал. Это одна из формулировок теорема о промежуточном значении.

Диадические интервалы

Диадические интервалы обладают следующими свойствами:

Следовательно, диадические интервалы имеют структуру, отражающую структуру бесконечного двоичное дерево.

Диадические интервалы важны для нескольких областей численного анализа, включая адаптивное уточнение сетки, многосеточные методы и вейвлет-анализ. Другой способ представить такую ​​структуру: p-адический анализ (для п = 2 ). [8]

Обобщения

Многомерные интервалы

Сложные интервалы

Топологическая алгебра

Это линейное отображение плоскости, которое составляет изоморфизм колец, придает плоскости мультипликативную структуру, имеющую некоторые аналогии с обычной комплексной арифметикой, например полярное разложение.

Источник