Формула скорости — обозначение, единицы измерения и примеры нахождения
Довольно часто в точных науках приходится сталкиваться с понятием скорость. Формула, дающаяся в школе на уроке математики, справедлива лишь для частного случая, при котором перемещение остаётся всегда постоянным. По сути, термин обозначает быстроту изменения чего-либо. Существует несколько видов движения и методов расчета.
Понятие и основные термины
Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.
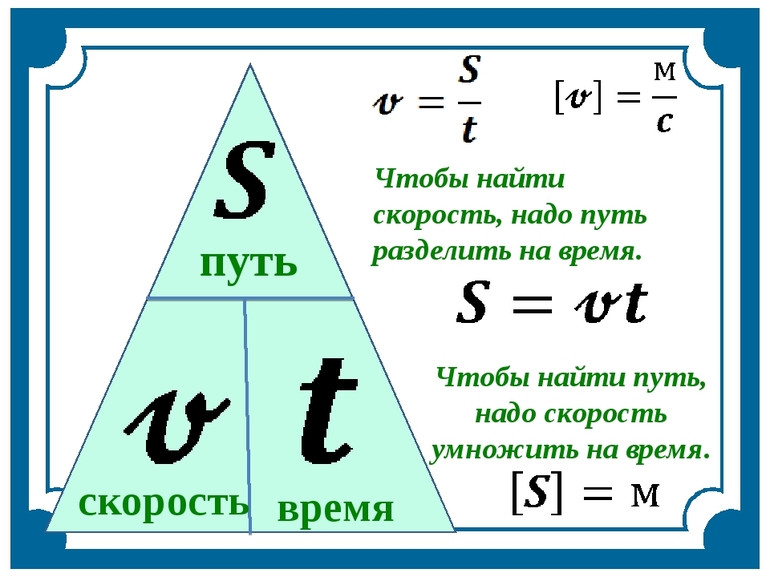
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:
Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.
Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.
Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:
Равноускоренное движение
Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.
Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.
В произвольно взятой точке скорость перемещения равна ускорению свободного падения.
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:
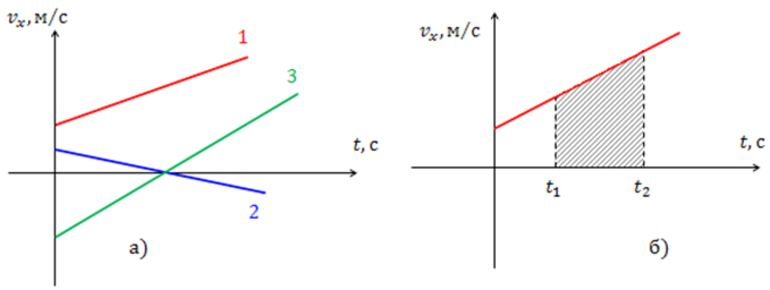
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.
По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство:
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
Угловая скорость
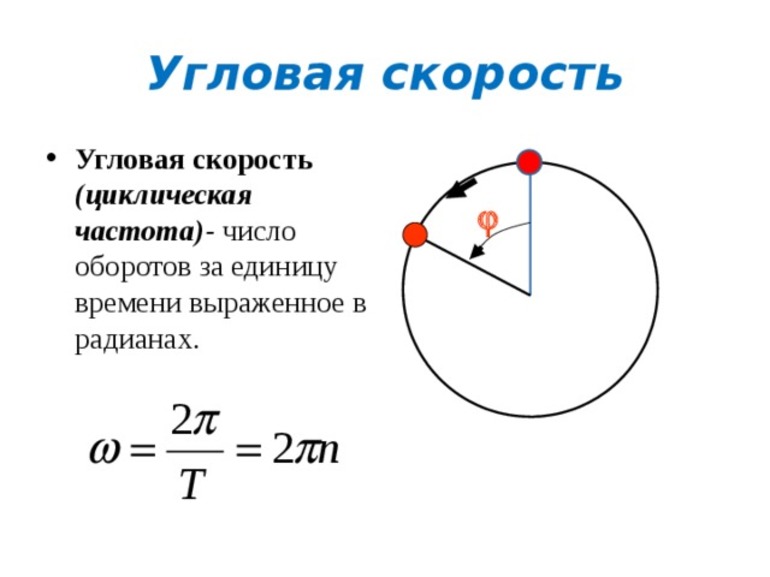
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.
В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.
Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).
Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.
Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.
Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Использование онлайн-калькулятора
В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.
Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.
Из множества сайтов можно выделить три наиболее популярных среди потребителей:
Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.
Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.
Понятие и основные термины
Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:
Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.
Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.
Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:
Равноускоренное движение
Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.
Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.
В произвольно взятой точке скорость перемещения равна ускорению свободного падения.
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.
По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство:
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
Угловая скорость
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.
В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.
Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).
Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.
Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.
Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Использование онлайн-калькулятора
В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.
Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.
Из множества сайтов можно выделить три наиболее популярных среди потребителей:
Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.
Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.
Основная особенность используемых в настоящее время систем единиц состоит в том, что между единицами разных величин имеются определенные соотношения. Эти соотношения установлены теми физическими законами (определениями), которыми связываются между собой измеряемые величины. Так, единица скорости выбрана таким образом, что она выражается через единицы расстояния и времени. При выборе единиц скорости используется определение скорости. Единицу силы, например, устанавливают при помощи второго закона Ньютона.
При построении определенной системы единиц, выбирают несколько физических величин, единицы которых устанавливают независимо друг от друга. Единицы таких величин называют основными. Единицы остальных величин выражают через основные, их называют производными.
Таблица единиц измерения «Пространство и время»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
l, s, d
Протяжённость объекта в одном измерении.
Протяженность объекта в двух измерениях.
Протяжённость объекта в трёх измерениях.
α, φ
Величина изменения направления.
α, β, γ
Быстрота изменения координат тела.
метр в секунду в квадрате
м/с 2
Быстрота изменения скорости объекта.
рад/с =
Скорость изменения угла.
радиан на секунду в квадрате
рад/с 2 =
Быстрота изменения угловой скорости
Таблица единиц измерения «Механика»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Величина, определяющая инерционные и гравитационные свойства тел.
килограмм на кубический метр
кг/м 3
Масса на единицу объёма.
Масса на единицу площади.
кг/м 2
Отношение массы тела к площади его поверхности
Масса на единицу длины.
Отношение массы тела к его линейному параметру
кубический метр на килограмм
м 3 /кг
Объём, занимаемый единицей массы вещества
килограмм в секунду
Масса вещества, которая проходит через заданную площадь поперечного сечения потока за единицу времени
кубический метр в секунду
м 3 /с
Объёмный расход жидкости или газа
килограмм-метр в секунду
кг•м/с
Произведение массы и скорости тела.
экстенсивная, сохраняющаяся величина
килограмм-метр в квадрате в секунду
кг•м 2 /с
Мера вращения объекта.
килограмм-метр в квадрате
кг•м 2
Мера инертности объекта при вращении.
Действующая на объект внешняя причина ускорения.
Произведение силы на длину перпендикуляра, опущенного из точки на линию действия силы.
Произведение силы на время её действия
Давление, механическое напряжение
Па = (кг/(м·с 2 ))
Сила, приходящаяся на единицу площади.
Дж = (кг·м 2 /с 2 )
Скалярное произведение силы и перемещения.
Дж = (кг·м 2 /с 2 )
Способность тела или системы совершать работу.
экстенсивная, сохраняющаяся величина, скаляр
Вт = (кг·м 2 /с 3 )
Скорость изменения энергии.
Таблица единиц измерения «Периодические явления, колебания и волны»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Промежуток времени, за который система совершает одно полное колебание
Частота периодического процесса
Число повторений события за единицу времени.
Циклическая (круговая) частота
рад/с
Циклическая частота электромагнитных колебаний в колебательном контуре.
секунда в минус первой степени
Периодический процесс, равный числу полных циклов, совершённых за единицу времени.
Расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
метр в минус первой степени
Пространственная частота волны
Таблица единиц измерения «Тепловые явления»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Средняя кинетическая энергия частиц объекта.
кельвин в минус первой степени
Зависимость электрического сопротивления от температуры
gradT
Изменение температуры на единицу длины в направлении распространения теплоты.
Теплота (количество теплоты)
Дж = (кг·м 2 /с 2 )
Энергия, передаваемая от одного тела к другому немеханическим путём
джоуль на килограмм
Дж/кг
Кол-во теплоты, которое необходимо подвести к веществу, взятому при температуре плавления, чтобы расплавить его.
Кол-во теплоты, поглощаемой (выделяемой) телом в процессе нагревания.
джоуль на килограмм-кельвин
Дж/(кг•К)
Теплоёмкость единичной массы вещества.
джоуль на килограмм
Дж/кг
Мера необратимого рассеивания энергии или бесполезности энергии.
Таблица единиц измерения «Молекулярная физика»
Физическая величина
Символ
Единица измерения физической величины
Описание
Примечания
моль
Количество однотипных структурных единиц, из которых состоит вещество.
M, μ
кг/моль
Отношение массы вещества к количеству молей этого вещества.
Дж/моль
Энергия термодинамической системы.
джоуль на моль-кельвин
Дж/(моль•К)
Теплоёмкость одного моля вещества.
метр в минус третьей степени
Число молекул, содержащихся в единице объема.
килограмм на кубический метр
кг/м 3
Отношение массы компонента, содержащегося в смеси, к объёму смеси.
моль на кубический метр
моль/м 3
Содержание компонента относительно всей смеси.
В, μ
квадратный метр на вольт-секунду
м 2 /(В•с)
Коэффициент пропорциональности между дрейфовой скоростью носителей и приложенным внешним электрическим полем.
Таблица единиц измерения «Электричество и магнетизм»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Протекающий в единицу времени заряд.
ампер на квадратный метр
А/м 2
Сила электрического тока, протекающего через элемент поверхности единичной площади.
Кл = (А·с)
Способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.
экстенсивная, сохраняющаяся величина
Электрический дипольный момент
Электрические свойства системы заряженных частиц в смысле создаваемого ею поля и действия на неё внешних полей.
кулон на квадратный метр
Кл/м 2
Процессы и состояния, связанные с разделением каких-либо объектов, преимущественно в пространстве.
Изменение потенциальной энергии, приходящееся на единицу заряда.
Работа сторонних сил (некулоновских) по перемещению заряда.
Отношение силы F, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда q
Мера способности проводника накапливать электрический заряд
Ом = (м 2 ·кг/(с 3 ·А 2 ))
сопротивление объекта прохождению электрического тока
Удельное электрическое сопротивление
Способность материала препятствовать прохождению электрического тока
Способность тела (среды) проводить электрический ток
Векторная величина, являющаяся силовой характеристикой магнитного поля
Величина, учитывающая интенсивность магнитного поля и занимаемую им область.
Напряженность магнитного поля
Разность вектора магнитной индукции B и вектора намагниченности M
А•м 2
Величина, характеризующая магнитные свойства вещества
Величина, характеризующая магнитное состояние макроскопического физического тела.
Коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и полным магнитным потоком
Дж = (кг·м 2 /с 2 )
Энергия, заключенная в электромагнитном поле
Объемная плотность энергии
джоуль на кубический метр
Дж/м 3
Энергия электрического поля конденсатора
Мощность в цепи переменного тока
Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока
Суммарная мощность с учетом активной и реактивной ее составляющих, а также отклонения формы тока и напряжения от гармонической
Таблица единиц измерения «Оптика, электромагнитное излучение»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Количество световой энергии, излучаемой в заданном направлении в единицу времени.
Световая, экстенсивная величина
Физическая величина, характеризующая количество «световой» мощности в соответствующем потоке излучения
Физическая величина, характеризует способность энергии, переносимой светом, вызывать у человека зрительные ощущения
Отношение светового потока, падающего на малый участок поверхности, к его площади.
люмен на квадратный метр
лм/м 2
Световая величина, представляющая собой световой поток
кандела на квадратный метр
кд/м 2
Сила света, излучаемая единицей площади поверхности в определенном направлении
Дж = (кг·м 2 /с 2 )
Энергия, переносимая оптическим излучением
Таблица единиц измерения «Акустика»
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Переменное избыточное давление, возникающее в упругой среде при прохождении через неё звуковой волны
кубический метр в секунду
м 3 /с
Отношение объема сырья, подаваемого в реактор в час к объему катализатора
Скорость распространения упругих волн в среде
ватт на квадратный метр
Вт/м 2
Величина, характеризующая мощность, переносимую звуковой волной в направлении распространения
скалярная физическая величина
паскаль-секунда на кубический метр
Па•с/м 3
Отношение амплитуды звукового давления в среде к колебательной скорости её частиц при прохождении через среду звуковой волны
ньютон-секунда на метр
Указывает силу, необходимую для движения тела при каждой частоте
Физическая величина
Символ
Единица измерения физической величины
Ед. изм. физ. вел.
Описание
Примечания
Масса объекта, находящегося в состоянии покоя.
Величина, выражающая влияние внутренних взаимодействий на массу составной частицы
Элементарный электрический заряд
Минимальная порция (квант) электрического заряда, наблюдающегося в природе у свободных долгоживущих частиц
Дж = (кг·м 2 /с 2 )
Разность между энергией состояния, в котором составляющие части системы бесконечно удалены
Период полураспада, среднее время жизни
Время, в течение которого система распадается в примерном отношении 1/2
Величина, характеризующая вероятность взаимодействия элементарной частицы с атомным ядром или другой частицей
Величина, равная отношению общего числа распадов радиоактивных ядер нуклида в источнике ко времени распада
Энергия ионизирующего излучения
Дж = (кг·м 2 /с 2 )
Вид энергии, высвобождаемой атомами в форме электромагнитных волн (гамма- или рентгеновское излучение) или частиц
Поглощенная доза ионизирующего излучения
Доза, при которой массе 1 кг передаётся энергия ионизирующего излучения в 1 джоул
Эквивалентная доза ионизирующего излучения
Поглощенная доза любого ионизирующего излучения, равная 100 эрг на 1 грамм облученного вещества
Экспозиционная доза рентгеновского и гамма-излучения
кулон на килограмм
Кл/кг
отношение суммарного электрического заряда ионов одного знака от внешнего гамма-излучения
Обозначения в физике с несколькими буквами
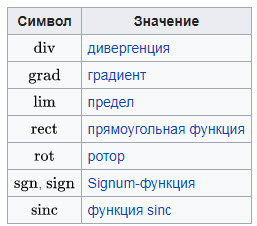
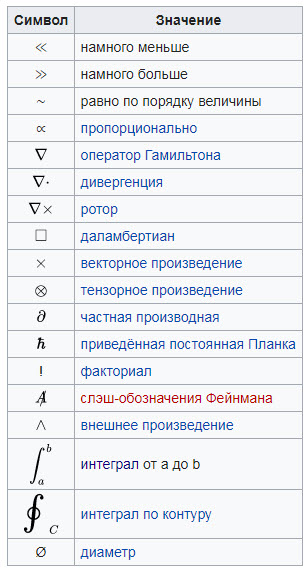
Специальные символы
Для удобства написания и чтения в среде ученых физиков принято использовать специальные символы, характеризующие те или иные явления и свойства.
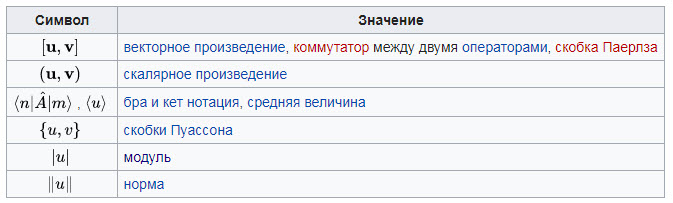
Скобки
В физике принято использовать не только формулы, которые применяют в математике, но и специализированные скобки.
Диакритические знаки
Диакритические знаки добавляются к символу физической величины для обозначения определённых различий. Ниже диакритические знаки добавлены для примера к букве x.