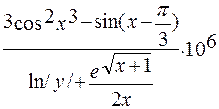Основные математические функции MatLab
В ML существует большое количество элементарных математических функций для выполнения действий с числами: тригонометрические, степенные, логарифмические, экспоненциальные и функции округления. Каждая функция обладает именем и списком аргументов, которые задаются в круглых скобках и, если их несколько, перечисляются через запятую.
Существуют встроенные тригонометрические и гиперболические функции: sin(x), cos(x), tan(x), cot(x), asin(x), acos(x), atan(x), acot(x), sinh(x) и т.д. Аргументы этих функций (в следующих версиях, начиная с версии 7.0) могут задаваться в радианах и градусах. У функций в градусной мере после названия добавляется буква d. sin(x) – аргумент в радианах, а sind(x) – аргумент в градусах.
Некоторые часто используемые математические функции:
· exp(x)–экспонента числа x;
· log(x)– натуральный логарифм;
· log10(x)– десятичный логарифм;
· sqrt(x)– квадратный корень;
· abs(x)– абсолютное значение x;
· mod(x, y)– остаток от целочисленного деления с учетом знака;
· rem(x, y)– остаток от целочисленного деления без учета знака;
· real(z)– вещественная часть комплексного числа;
· imag(z)– мнимая часть комплексного числа;
· round(x)– округление до ближайшего целого.
Более полный список основных математических функций MatLab:
| sqrt(x) | вычисление квадратного корня |
| exp(x) | возведение в степень числа e |
| pow2(x) | возведение в степень числа 2 |
| log(x) | вычисление натурального логарифма |
| log10(x) | вычисление десятичного логарифма |
| log2(x) | вычисление логарифма по основанию 2 |
| sin(x) | синус угла x, заданного в радианах |
| cos(x) | косинус угла x, заданного в радианах |
| tan(x) | тангенс угла x, заданного в радианах |
| cot(x) | котангенс угла x, заданного в радианах |
| asin(x) | арксинус |
| acos(x) | арккосинус |
| atan(x) | арктангенс |
| pi | число пи |
| round(x) | округление до ближайшего целого |
| fix(x) | усечение дробной части числа |
| floor(x) | округление до меньшего целого |
| ceil(x) | округление до большего целого |
| mod(x,y) | остаток от деления с учётом знака |
| sign(x) | знак числа |
| factor(x) | разложение числа на простые множители |
| isprime(x) | истинно, если число простое |
| rand | генерация псевдослучайного числа с равномерным законом распределения |
| randn | генерация псевдослучайного числа с нормальным законом распределения |
| abs(x) | вычисление модуля числа |
С использованием вышеупомянутых функций, записать и сосчитать значение арифметического выражения:
Вычислить: res=
Составление арифметического выражения лучше всего начинать с расстановки основных скобок выражения. Причем открытую скобку следует сразу закрывать и продолжать набор формулы внутри скобок. В этом случае число открывающих скобок будет равно числу закрывающих, и вероятность ошибки будет минимальной.
Если в выражении многократно встречаются одинаковые фрагменты, то их целесообразно вычислять 1 раз и результат помещать в отдельные переменные. Это позволяет избежать одинаковых вычислений и тем самым оптимизирует вычисления.
res=(3*cos(x^3)^2-sin(x-pi/3))/(log(abs(y))+exp (sqrt (x+1))/(2*x))*1E6
Для эффективной работы с большими наборами данных или при необходимости многократных вычислений рассмотренных средств недостаточно. В ML существует возможность записать последовательность команд в файл, сохранить его, дать ему имя и выполнить, набрав в командной строке имя файла. Это можно сделать во встроенном редакторе системы. Такие файлы называются файлами-сценариями или скрипт-файлами. При сохранении они автоматически получают расширение системы – m.
Файлы-программы (их называют скриптами или сценариями) являются самым простым типом m-файлов. Script-файл состоит из последовательности команд, не содержит заголовка, а также входных и выходных параметров. Все объекты, используемые внутри script-файла, считаются глобальными. Если в рабочем пространстве есть данные, то внутри script-файла их можно использовать, а по окончании его выполнения использовать данные, созданные с его помощью. Такие файлы используются для автоматизации выполнения большого набора инструкций. Их текст набирают в окне встроенного редактора ML.
Для выполнения файла-программы достаточно в командной строке указать имя этого скрипта. Перед запуском программы на выполнение необходимо установить нужный каталог в качестве текущего. Запуск файла на выполнение можно осуществить двумя способами: из окна редактора и из командного окна.
Для запуска программы на выполнение из окна редактора надо выбрать пункт меню Debug, Run или нажать функциональную клавишу F5, или выбрать соответствующую пиктограмму на панели инструментов. Выполнить программу, уже сохраненную на диске, можно из командного окна ML, просто набрав имя файла без расширения.
Дата добавления: 2016-04-02 ; просмотров: 5524 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Основные математические функции MatLab



MatLab содержит в себе все распространенные математические функции, которые доступны по их имени при реализации алгоритмов. Например, функция sqrt() позволяет вычислять квадрат числа и может быть использована в программе следующим образом:
Аналогичным образом вызываются и все другие математические функции, представленные в табл. 1.2.
Таблица 1.2. Основные математические функции MatLab
| sqrt(x) | вычисление квадратного корня |
| exp(x) | возведение в степень числа e |
| pow2(x) | возведение в степень числа 2 |
| log(x) | вычисление натурального логарифма |
| log10(x) | вычисление десятичного логарифма |
| log2(x) | вычисление логарифма по основанию 2 |
| sin(x) | синус угла x, заданного в радианах |
| cos(x) | косинус угла x, заданного в радианах |
| tan(x) | тангенс угла x, заданного в радианах |
| cot(x) | котангенс угла x, заданного в радианах |
| asin(x) | арксинус |
| acos(x) | арккосинус |
| atan(x) | арктангенс |
| pi | число пи |
| round(x) | округление до ближайшего целого |
| fix(x) | усечение дробной части числа |
| floor(x) | округление до меньшего целого |
| ceil(x) | округление до большего целого |
| mod(x) | остаток от деления с учётом знака |
| sign(x) | знак числа |
| factor(x) | разложение числа на простые множители |
| isprime(x) | истинно, если число простое |
| rand | генерация псевдослучайного числа с равномерным законом распределения |
| randn | генерация псевдослучайного числа с нормальным законом распределения |
| abs(x) | вычисление модуля числа |
Почти все элементарные функции допускают вычисления и с комплексными аргументами. Например:
Ниже показан пример задания вектора с именем a, и содержащий значения 1, 2, 3, 4:
a = [1 2 3 4]; % вектор-строка
Для доступа к тому или иному элементу вектора используется следующая конструкция языка:
disp( a(1) ); % отображение значения 1-го элемента вектора
disp( a(2) ); % отображение значения 2-го элемента вектора
disp( a(3) ); % отображение значения 3-го элемента вектора
disp( a(4) ); % отображение значения 4-го элемента вектора
т.е. нужно указать имя вектора и в круглых скобках написать номер индекса элемента, с которым предполагается работать. Например, для изменения значения 2-го элемента массива на 10 достаточно записать
a(2) = 10; % изменение значения 2-го элемента на 10
Часто возникает необходимость определения общего числа элементов в векторе, т.е. определения его размера. Это можно сделать, воспользовавшись функцией length() следующим образом:
N = length(a); % (N=4) число элементов массива а
Если требуется задать вектор-столбец, то это можно сделать так
a = [1; 2; 3; 4]; % вектор-столбец
b = [1 2 3 4]’; % вектор-столбец
при этом доступ к элементам векторов осуществляется также как и для векторов-строк.
Следует отметить, что векторы можно составлять не только из отдельных чисел или переменных, но и из векторов. Например, следующий фрагмент программы показывает, как можно создавать один вектор на основе другого:
a = [1 2 3 4]; % начальный вектор a = [1 2 3 4]
b = [a 5 6]; % второй вектор b = [1 2 3 4 5 6]
Здесь вектор b состоит из шести элементов и создан на основе вектора а. Используя этот прием, можно осуществлять увеличение размера векторов в процессе работы программы:
a = [a 5]; % увеличение вектора а на один элемент
Недостатком описанного способа задания (инициализации) векторов является сложность определения векторов больших размеров, состоящих, например, из 100 или 1000 элементов. Чтобы решить данную задачу, в MatLab существуют функции инициализации векторов нулями, единицами или случайными значениями:
a1 = zeros(1, 100); % вектор-строка, 100 элементов с
% нулевыми значениями
a2 = zeros(100, 1); % вектор-столбец, 100 элементов с
% нулевыми значениями
a3 = ones(1, 1000); % вектор-строка, 1000 элементов с
% единичными значениями
a4 = ones(1000, 1); % вектор-столбец, 1000 элементов с
% единичными значениями
a5 = rand(1000, 1); % вектор-столбец, 1000 элементов со
% случайными значениями
Матрицы в MatLab задаются аналогично векторам с той лишь разницей, что указываются обе размерности. Приведем пример инициализации единичной матрицы размером 3х3:
E = [1 0 0; 0 1 0; 0 01]; % единичная матрица 3х3
E = [1 0 0
0 1 0
0 0 1]; % единичная матрица 3х3
Аналогичным образом можно задавать любые другие матрицы, а также использовать приведенные выше функции zeros(), ones() и rand(), например:
A1 = zeros(10,10); % нулевая матрица 10х10 элементов

A2 = zeros(10); % нулевая матрица 10х10 элементов
A3 = ones(5); % матрица 5х5, состоящая из единиц
A4 = rand(100); % матрица 100х100, из случайных чисел
Для доступа к элементам матрицы применяется такой же синтаксис как и для векторов, но с указанием строки и столбца где находится требуемый элемент:
A = [1 2 3;4 5 6;7 8 9]; % матрица 3х3
disp( A(2,1) ); % вывод на экран элемента, стоящего во
% второй строке первого столбца, т.е. 4
disp( A(1,2) ); % вывод на экран элемента, стоящего в
% первой строке второго столбца, т.е. 2
Также возможны операции выделения указанной части матрицы, например:
B1 = A(:,1); % B1 = [1; 4; 7] – выделение первого столбца
B2 = A(2,:); % B2 = [1 2 3] – выделение первой строки
B3 = A(1:2,2:3); % B3 = [2 3; 5 6] – выделение первых двух
% строк и 2-го и 3-го столбцов матрицы А.
Размерность любой матрицы или вектора в MatLab можно определить с помощью функции size(), которая возвращает число строк и столбцов переменной, указанной в качестве аргумента:
a = 5; % переменная а
A = [1 2 3]; % вектор-строка
B = [1 2 3; 4 5 6]; % матрица 2х3
size(a) % 1х1
size(A) % 1х3
size(B) % 2х3
12. Тригонометрические и обратные им функции
Тригонометрические и обратные им функции
В системе MATLAB определены следующие тригонометрические и обратные тригонометрические функции. Функции вычисляются для каждого элемента массива. Входной массив допускает комплексные значения. Напоминаем, что все углы в функциях задаются в радианах.
Э acos (X) — возвращает арккосинус для каждого элемента X. Для действительных значений X в области [-1, 1] acos(X) возвращает действительное значение из диапазона диапазона [0, р], для действительных значений X вне области [-1, 1] acos(X) возвращает комплексное число.
acot (X) — возвращает арккотангенс для каждого элемента X. Пример:
acsc(X) — возвращает арккосеканс для каждого элемента X. Пример:
asec(X) — возвращает арксеканс для каждого элемента X. Пример:
asin(X) — возвращает арксинус для каждого элемента X. Для действительных значений X в области [-1, 1] asin(X) возвращает действительное число из диапазона [-р/2, р/2], для действительных значений X вне области [-1, 1] asin(X) возвращает комплексное число. Пример:
atan(X) — возвращает арктангенс для каждого элемента X. Для действительных значений X atan(X) находится в области [-р/2, р/2]. Пример:
atan2 (Y, X) — возвращает массив Р той же размерности, что X и Y, содержащий поэлементно арктангенсы отношения вещественных частей Y и X. Мнимые части игнорируются. Элементы Р находятся в интервале [-р, р]. Специфический квадрант определен функциями sign(Y) и sign(X). Это отличает полученный результат от результата atan(Y/X), который ограничен интервалом [-л/2, л/2].
cos(X) — возвращает косинус для каждого элемента X. Пример:
cot(X) — возвращает котангенс для каждого элемента X. Пример:
csc(X) — возвращает косеканс для каждого элемента X. Пример:
sec(X) — возвращает массив той же размерности что и X, состоящий из секансов элементов X. Пример:
sin(X) — возвращает синус для каждого элемента X. Пример:
1.0000 0.7071 0.5000 0.0000
tan(X) — возвращает тангенс для каждого элемента X.
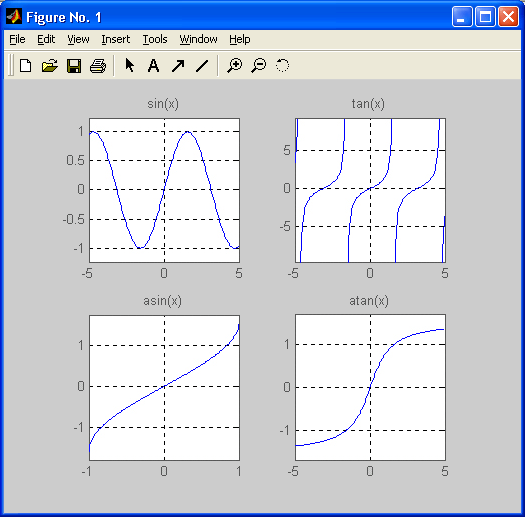
Рис. 8.2. Графики четырех тригонометрических функций
Следующий файл-сценарий позволяет наблюдать графики четырех тригонометрических функций (рис. 8.2):
syms xsubplot(2.2.1).ezplot(sin(x),[-5 5]).xlabel(«),gnd on
subplot(2.2.2),ezp»lot(tan(x).[-5 5]).xlabel(«).grid on
subplot(2,2,3),ezplot(asin(x),[-1 1]).grid on
subplot(2.2.4),ezplot(atan(x).[-5 5]),grid on
Поскольку многие тригонометрические функции периодичны, появляется возможность формирования из них любопытных комбинаций, позволяющих создавать типовые тестовые сигналы, используемые при моделировании радиоэлектронных устройств. Следующий файл-сценарий строит графики для таких комбинаций, создающих из синусоиды три наиболее распространенных сигнала — прямоугольные, пилообразные и треугольные импульсы:[ В пакете расширения Signal Processing Toolbox есть специальные функции для генерации таких сигналов — square и sawtooth. — Примеч. ред. ]
Соответствующие графики представлены на рис. 8.3.
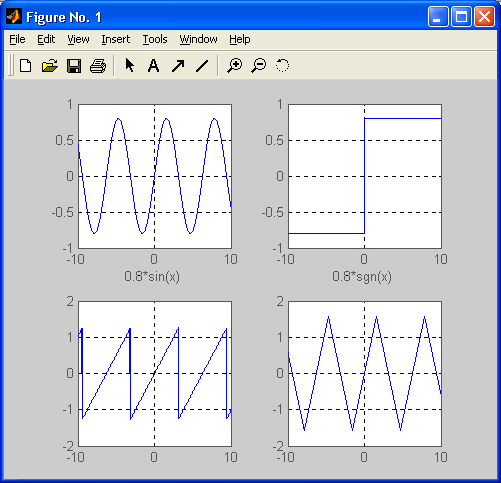
Рис. 8.3. Графики синусоиды, прямоугольных, пилообразных и треугольных колебаний
Дополнительный ряд графиков, полученных комбинациями элементарных функций, показан на рис. 8.4. Эти графики строятся следующим файлом-сценарием:
subplot(2.2.1).plot(x.sin(x). A 3).x1abel(‘sin(xr3’)
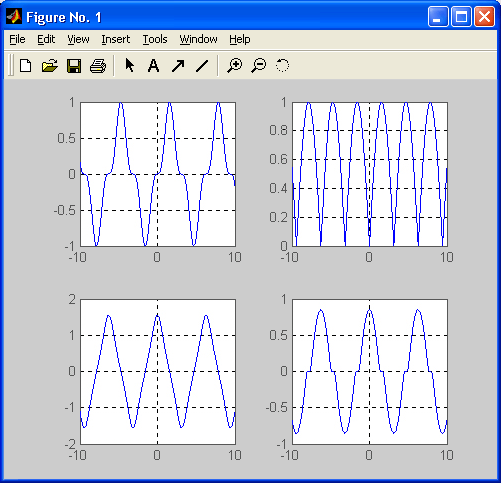
Рис. 8.4. Графики периодических сигналов без разрывов
Эти графики неплохо моделируют сигналы, получаемые при выпрямлении синусоидального напряжения (или тока) и при прохождении синусоидальных сигналов через нелинейные цепи.
Документация
Тангенс аргумента в радианах
Синтаксис
Описание
Примеры
Графическое изображение функции тангенса
Касательная вектора комплексных углов
Входные параметры
X — Введите угол в радианах
скаляр | вектор | матрица | многомерный массив
Введите угол в радианах в виде скаляра, вектора, матрицы или многомерного массива.
Типы данных: single | double
Поддержка комплексного числа: Да
Выходные аргументы
Y — Касательная входного угла
скаляр | вектор | матрица | многомерный массив
Касательная входного угла, возвращенного как скаляр с комплексным знаком или с действительным знаком, вектор, матричный или многомерный массив.
Больше о
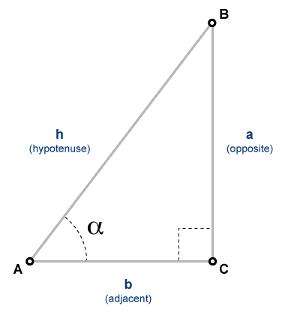
Функция тангенса
Касательная угла, α, заданный со ссылкой на право повернула, треугольник
Касательная сложного аргумента, α,
Советы
Расширенные возможности
«Высокие» массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.
Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.
Генерация кода графического процессора
Сгенерируйте код CUDA® для NVIDIA® графические процессоры с помощью GPU Coder™.
Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.
Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.
Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.
Смотрите также
Открытый пример
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
Документация MATLAB
Поддержка
© 1994-2021 The MathWorks, Inc.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.
Основные математические функции в MATLAB
Дата добавления: 2014-11-28 ; просмотров: 9359 ; Нарушение авторских прав
| № п/п | Математическая функция | Функция в MATLAB | № п/п | Математическая функция | Функция в MATLAB |
| sin(x) | sin(x) | arcsin(x) | asin(x) | ||
| cos(x) | cos(x) | arccos(x) | acos(x) | ||
| tg(x) | tan(x) | arctg(x) | atan(x) | ||
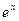 | exp(x) | sinh(x) | sinh(x) | ||
| ln(x) | log(x) | cosh(x) | cosh(x) | ||
| lg(x) | log10(x) | tgh(x) | tgh(x) | ||
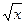 | sqrt(x) | arcsinh(x) | asinh(x) | ||
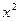 | x^2 | arccosh(x) | acosh(x) | ||
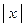 | abs(x) | arctgh(x) | atanh(x) |
Редактор Т.А. Жирнова
ИД № 06039 от 12.10.01
Свод. темплан 2006 г.
Подписано в печать 25.07.06. Формат 60х84 1/16. Бумага офсетная.
Отпечатано на дупликаторе. Усл. печ. л. 5,0. Уч.- изд. л. 5,0.
Издательство ОмГТУ. 644050, Омск, пр. Мира, 11.