Мощность алфавита в информатике
Понятие алфавита в информатике немного отличается от того, что изучают дети в первом классе. Здесь так называют знаковую систему, при помощи которой может быть передано информационное сообщение. Оно состоит из символов — минимально значимых составляющих, которые являются неделимыми. Одним из важнейших терминов в этой области является мощность алфавита.
Описание термина
Понятие мощности алфавита находится в основании изучения информатики. Алфавитом принято называть набор многочисленных символов. Сумма всех их в определённом языке и есть алфавитная мощность. Иными словами, это количество всех символов, входящих в конкретно взятый язык. Сюда входят не только буквы, но и прочие обозначения, в частности:
Это определение считается обобщённым и не принимает во внимание вычисления информационной составляющей сообщения. Она может содержать в себе числа, знаки препинания и прочее. В этом случае прибегают к использованию другого способа. Его суть основывается на том, что любая буква, цифра или знак обладают собственным информационным объемом данных. Компьютер работает с этим информационным кодом и распознает то, что было написано.
Основным постулатом в информатике является тот факт, что устройство разбирает введённую информацию исключительно в двоичном коде в форме нуля и единицы. В итоге получается, что абсолютно любой символ алфавита может быть успешно закодирован при помощи соответствующего подбора этих двух цифровых символов. Самая маленькая последовательность, применяемая при обозначении какой-либо цифры, буквы или другого знака, состоит из двух элементов.
Информационная масса отдельно взятого символа обычно изображается в форме информационной стандартной измерительной единицы, которая называется «бит». Восемь битов становятся равны одному байту.
Отображение символов в двоичном коде
Алфавитная мощность может быть использована на практике только при наличии двоичного кода. В качестве примера можно использовать упрощённый алфавит, состоящий всего из четырёх символов. В этом случае разрядность их и информационное представление описываются следующим образом:
Из этого списка можно сделать вывод о том, что если алфавитная мощность равняется 4, то масса отдельного единичного символа будет составлять 2 бита. Если же есть алфавит, состоящий из 8 символов, то при подборе двоичного трёхзначного кода для него комбинационное количество будет следующим:
Иными словами, если алфавитная мощность равна 8, то вес отдельно взятого символа для двоичного трёхзначного кода составит 3 бита.
Вычисление мощности алфавита
Эта формула была изобретена американским инженером Ральфом Хартли более сотни лет тому назад. Она применяется для работы с равновероятными событиями и используется для определения мощности конкретного буквенного набора, которая обозначается буквой N (информационная масса или объём). n означает численность бит в словесной единице, иными словами, количество знаков внутри двоичного кода. Так, если n равен 1, то N тоже равен 1, при n = 2 N = 4, при n = 3 N = 8, при n = 4 N = 16.
Чтобы сформулировать теорию о численности информации в набранном словосочетании, пользуются формулой I=K*i. В этом случае К обозначает численность всех символов в предложении, а i — это информационная масса символа.
При ответе на вопрос, как найти мощность алфавита, нужно сказать, что в русском языке 33 буквы, поэтому это можно выразить как N = 33. Для сравнения, аналогичный показатель в английском, немецком и французском языках равняется 26, в испанском — 27. Венгерский язык, например, является 40-символьным.
Существует также и клавиатурный язык, куда входят не только буквы, но и дополнительные знаки. Так, в русском языке есть ещё 10 цифр и 11 символов, а также пробел и пара скобок. Их мощность прибавляется к аналогичному буквенному показателю, и на выходе получается N = 33+10+11+1+2=57. В некоторых случаях букву «ё» не выделяют в качестве отдельного самостоятельного символа, и в таком случае полная мощность русского алфавита становится равна 56.
Определение информационного объёма в тексте
Почти всегда при наборе текста на компьютерах и других электронных устройствах приходится сталкиваться с написанием различных символов. К ним следует отнести:
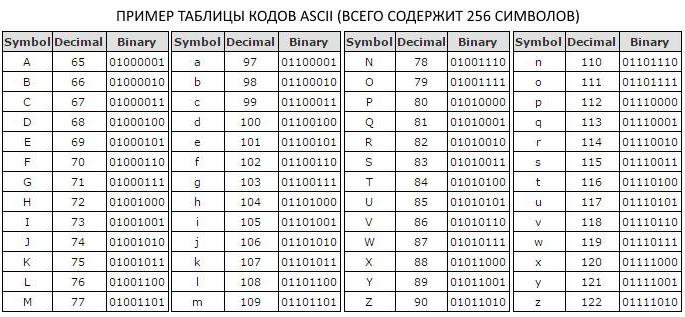
По всем расчётам получается, что мощность компьютерного алфавита составляет 256 различных символов и вариантов. В соответствии с формулой Хартли, N = 256, а i — масса любого из значков в клавиатурном алфавите соответствует одному байту, или восьми битам.
Размер любой напечатанной фразы может быть вычислен по формуле V=K ⋅ log2N. В этом случае N обозначает количество всех символов в алфавите, а K — это численность знаков непосредственно в напечатанной фразе. Так, например, имеется произвольный текст объёмом в 25 листов. На каждом из них расположено по 45 строчек текста, содержащих по 58 символов.
Исходя из этого, на любой отдельной странице будет 45*58 = 2610 байт информации. В целом же по всему тексту этот объём будет равен 2610*25 = 65250 байт. Для обозначения мощности алфавита в информатике общепринятым вариантом является буква N из формулы Хартли. Именно ее чаще всего указывают в большинстве учебников и профессиональной литературе.
В кодовой таблице ASCII используют восьмибитную кодировку текстовых сообщений. Она позволяет полностью вместить основной набор символов кириллического и латинского алфавитов как в строчном, так и в прописном вариантах. Также с её помощью можно отобразить знаки препинания, цифры и прочие базовые знаки. Часто пользователям приходится иметь дело с более крупными объёмами, состоящими из триллионов байтов.
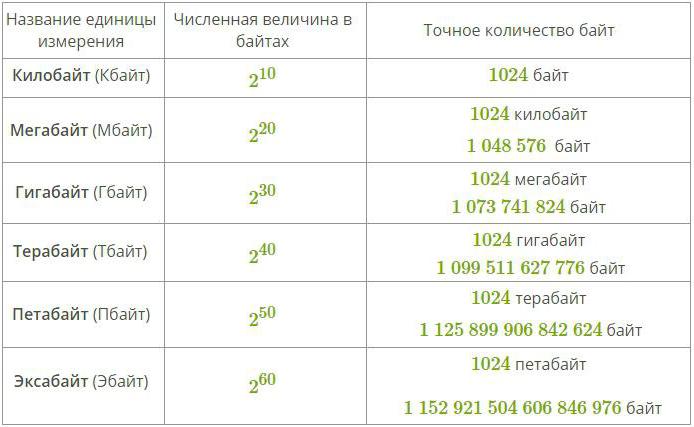
Для удобства их всегда переводят в увеличенные величины — кило-, мега-, гигабайты и прочее. Для их упрощённого обозначения используются специальные сокращения: Кб, Мб, Гб и так далее. 1 Кб равняется 1024 байтам (2 байта в десятой степени), 1 Мб составляет 1024 Кб (2 Кб в десятой степени) и так далее. Исходя из этого, 65250 байт будут составлять 63,72 килобайта.
Поскольку один отдельный символ состоит из 8 битов, то устанавливать их кодировку целиком не представляется возможным. Вместо этого предпочтительнее образовать кодировку трёхбитовых комбинаций. Расчёт этого действия проводится по формуле Хартли, где n-ная степень будет равняться трём. В результате получается N, равная 8.
При определении мощности чаще всего используют алфавитный подход. Он говорит о том, что объём информации, заложенной в тексте, зависит исключительно от мощности самого алфавита и размера сообщения (то есть количества символов, содержащихся в нём). Этот показатель не имеет никакой связи со смысловым наполнением для человека.
Примеры расчёта мощности
От пользователей или обучающихся в задачах часто требуют научиться определять информационный объём какого-либо сообщения, приняв информационный вес символа за один байт. Так, в отрывке из поэмы Н. Н. Некрасова «Крестьянские дети»:
Я из лесу вышел; был сильный мороз»
будет 67 символов вместе с пробелами, то есть, в соответствии с условиями задания, 67 байт. Их количество умножают на 8 (количество битов в байте), и на выходе получается 536 битов.
Таким образом, зная в теории суть мощности, можно без проблем определять информационный объем различных сообщений.
Что такое мощность алфавита
Алфавитом в информатике называется система знаков, с помощью которой можно подать информационное сообщение. Чтобы понять сущность этого определения, приведем немного дополнительных теоретических фактов:
Но на практике мы имеем следующее: компьютер не понимает, что такое буквы. Поэтому для передачи информационного сообщения его сначала нужно закодировать понятным компьютеру языком. Для того чтобы двигаться дальше, необходимо ввести дополнительные термины.
Что такое мощность алфавита
Под мощностью алфавита мы подразумеваем общее количество символов в нем. Для того чтобы узнать, какова мощность алфавита, необходимо просто посчитать количество символов в нем. Давайте разбираться. Для русского алфавита мощность алфавита равна 33 или же 32 символам, если не использовать «ё».
Давайте предположим, что все символы в нашем алфавите встречаются с равной вероятностью. Это предположение можно понимать так: допустим, у нас есть мешок с подписанными кубиками. Число кубиков в нем бесконечно, и каждый подписан лишь одним символом. Тогда при равномерном распределении, сколько бы мы кубиков ни доставали из мешка, количество кубиков с разными символами будет одинаково, или будет стремиться к этому при росте числа кубиков, которые мы достаем из мешка.
Оценка веса информационных сообщений
Почти сто лет назад американский инженер Ральф Хартли вывел формулу, с помощью которой можно оценивать количество информации в сообщении. Его формула работает для равновероятных событий и выглядит так:
Эта формула в общем виде задает связь между количеством равновероятных событий «M» и количеством информации «i».
Рассчитываем мощность
Скорее всего, вам уже известно из школьного курса информатики, что в современных вычислительных системах, построенных на архитектуре фон Неймана, используется двоичная система кодировки информации. Так кодируются как программы, так и данные.
Как измеряют информацию
Восьмибитная кодировка текстовых сообщений, которая используется в кодовой таблице ASCII, позволяет вместить базовый набор символов латиницы и кириллицы в прописном и строчном варианте, цифры, символы знаков препинания и другие базовые символы.
Для того чтобы измерять более крупные объемы данных, используют специальные приставки к словам байт и бит. Такие приставки приведены в таблице ниже:
Многие люди, изучавшие физику возразят, что рационально было бы использовать классические приставки для обозначения единиц информации (вроде кило- и мега-), но на самом деле это не совсем корректно, ведь такие префиксы к величинам обозначают умножение на ту или иную степень числа десять, когда в информатике везде используется двоичная система измерений.
Правильные названия единиц измерения данных
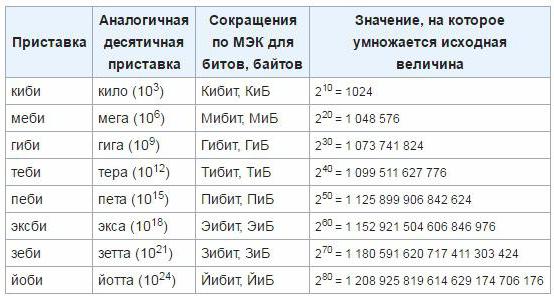
Для того чтобы устранить некорректности и неудобства, в марте 1999 года Международной комиссией в области электротехники были утверждены новые приставки к единицам, которые используются для определения объема информации в электронной вычислительной технике. Такими приставками стали «меби», «киби», «гиби», «теби», «эксби», «пети». Пока эти единицы еще не прижились, так что, скорее всего, необходимо время для введения этого стандарта и начала широкого применения. Как осуществлять переход от классических единиц к новоутвержденным, вы можете определить по следующей таблице:
Предположим, что мы имеем текст, который содержит K символов. Тогда, используя алфавитный подход, можно вычислить объем информации V, который в нем содержится. Он будет равен произведению мощности алфавита на информационный вес одного символа в нем.
По формуле Хартли мы знаем, как вычислить объем информации через двоичный логарифм. Предположив, что количество знаков алфавита равно N и количество знаков в записи информационного сообщения равняется K, получим такую формулу для вычисления информационного объема сообщения:
Алфавитный подход свидетельствует о том, что информационный объем будет зависеть только лишь от мощности алфавита и размера сообщений (то есть количества символов в нем), но никак не будет связан со смысловым содержанием для человека.
Примеры расчета мощности
На уроках информатики часто дают задачи на нахождение мощности алфавита, длины сообщения или информационного объема. Вот одна из таких задач:
«Текстовый файл занимает 11 Кбайт дискового пространства и содержит 11264 символа. Определите мощность алфавита данного текстового файла».
Каким будет решение, можно увидеть на картинке ниже.
Таким образом, алфавит мощностью 256 символов несет в себе всего лишь 8 бит информации, что в информатике называют одним байтом. Байт описывает 1 символ таблицы ASCII, что, если задуматься, совсем не много.
Современные хранилища данных вроде дата-центров Google и Facebook содержат не меньше, чем десятки петабайт информации. Точное количество данных, впрочем, трудно будет подсчитать даже им самим, ведь тогда нужно будет остановить все процессы на серверах и закрыть пользователям доступ к записи и редактированию их личной информации.
Но чтобы вообразить такие немыслимые объемы данных, необходимо четко понимать, что все складывается из маленьких деталей. Необходимо понимать, чему равна мощность алфавита (256) и сколько бит содержит 1 байт информации (как вы помните, 8).
Урок информатики и ИКТ «Измерение информации. Алфавитный подход»
Цель урока: познакомить с понятиями: “измерение информации”, “алфавит”, “мощность алфавита”, “алфавитный подход в измерении информации”, научить измерять информационный объём сообщений, с учётом информационного веса символов.
Тип урока: объяснительно-демонстрационный с элементами практикума.
Нагляднось: презентация “Измерение информации” (приложение 1).
Учебная литература: учебник “Информатика”. 8-й класс (базовый курс) И.Г.Семакин, “Информатика” задачник-практикум (1 часть) И.Г.Семакин.
Требования к знаниям и умениям:
II. Проверка домашнего задания.
Задачник-практикум № 1. с. 11 № 2, 5, 8, 11, 19 *.
III. Новый материал.
Процесс познания окружающего мира приводит к накоплению информации в форме знаний.
Как же узнать, много получено информации или нет?
Необходимо измерить объём информации. А как это сделать мы сегодня узнаем.
Получение новой информации приводит к расширению знаний или, как иначе можно сказать, к уменьшению неопределённости знания.
Если некоторое сообщение приводит к уменьшению неопределённости нашего знания, то можно сказать, что такое знание содержит информацию (рисунок 1).
2. Как можно измерить количество информации.
Для измерения различных величин существуют эталонные единицы измерения.
Следовательно, для измерения информации должна быть введена своя эталонная единица.
Существует два подхода к измерению информации:
а) Содержательный (вероятностный). Количество информации связывается с содержанием (смыслом) полученного сообщения или с учётом вероятности событий.
б) Алфавитный. Позволяет измерять информационный объём текста на любом языке (естественном или формальном), при использовании данного подхода объём информации не связывают с содержанием текста, в данном случае, объём зависит от информационного веса символов.
3. Алфавитный подход к измерению информации.
*Алфавит включают и пробел (пропуск между словами).
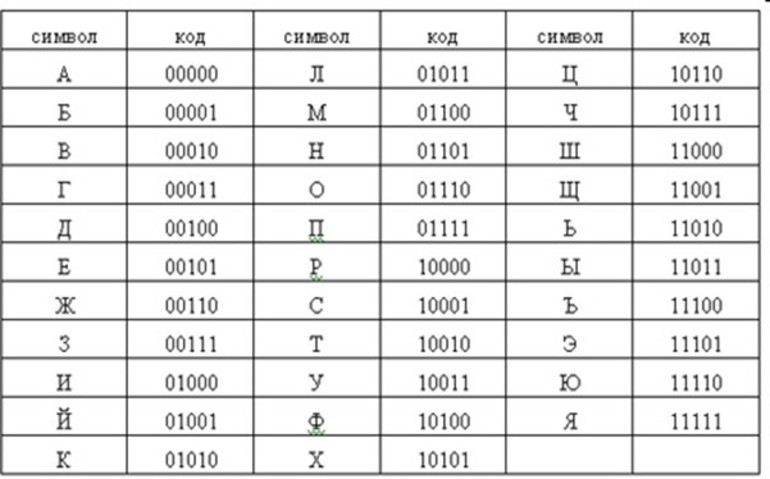
Например: мощность алфавита русских букв и используемых символов равна 54:
33 буквы + 10 цифр + 11 знаков препинания, скобки, пробел.
Наименьшую мощность имеет алфавит, используемый в компьютере (машинный язык), его называют двоичным алфавитом, т.к. он содержит только два знака “0”, “1”.
Информационный вес символа двоичного алфавита принят за единицу измерения информации и называется 1 бит.
Попробуйте определить объём информационного сообщения:
Информация, записанная на машинном языке, весит:
При алфавитном подходе считают, что каждый символ текста, имеет информационный вес.
Информационный вес символа зависит от мощности алфавита.
С увеличением мощности алфавита, увеличивается информационный вес каждого символа.
Для измерения объёма информации необходимо определить сколько раз информация равная 1 биту содержится в определяемом объёме информации.
1) Возьмём четырёхзначный алфавит (придуманный), (рисунок 2).
Все символы исходного алфавита можно закодировать всеми возможными комбинациями, используя цифры двоичного алфавита.
Получим двоичный код каждого символа алфавита. Для того чтобы закодировать символы алфавита мощность которого равна четырём, нам понадобится два символа двоичного кода.
Следовательно, каждый символ четырёхзначного алфавита весит 2 бита.
Вывод. Весь алфавит, мощность которого равна 8 можно закодировать на машинном языке с помощью трёх символов двоичного алфавита (рисунок 4).
— Как вы думаете, каков информационный объём каждого символа восьмизначного алфавита?
Каждый символ восьмизначного алфавита весит 3 бита.
3). Закодируйте с помощью двоичного кода каждый символ алфавита, мощность которого равна 16.
— Какой можно сделать вывод?
Алфавит из шестнадцати символов можно закодировать с помощью четырёхзначного двоичного кода.
Задача: Какой объём информации содержат 3 символа 16 – символьного алфавита?
Так как каждый символ алфавита мощностью 16 знаков можно закодировать с помощью четырёхзначного двоичного кода, каждый символ исходного алфавита весит 4 бита.
Так как всего использовали 3 символа алфавита мощностью 16 символов, следовательно: 4 бит • 3 = 12 бит
Ответ: объём информации записанный 3 знаками алфавита мощностью 16 символов равен 12 бит.
— Найдите закономерность (рисунок 5)!
— Какой вывод можно сделать?
Информационный вес каждого символа, выраженный в битах (b), и мощность алфавита (N) связаны между собой формулой: N = 2 b
Алфавит, из которого составляется на компьютере текст (документ) состоит из 256 символов.
Этот алфавит содержит символы: строчные и прописные латинские и русские буквы, цифры, знаки арифметических операций, всевозможные скобки, знаки препинания и другие символы.
— Узнайте, какой объём информации содержится в одном символе алфавита, мощность которого равна 256.
Вывод. Значит, каждый символ алфавита используемого в компьютере для печати документов весит 8 бит.
Эту величину приняли так же за единицу измерения информации и дали название байт.
1) На каждой странице 50 • 40 = 2000 символов;
2) во всей статье 2000 • 30 = 60000 символов;
3) т.к. вес каждого символа равен 1 байту, следовательно, информационный объём всей статьи 60000 • 1 = 60000 байт или 60000 • 8 = 480000 бит.
— Как видно из задачи байт “мелкая” единица измерения информационного объёма текста, поэтому для измерения больших объёмов информации используются более крупные единицы.
Единицы измерения информационного объёма:
1 килобайт = 1 Кб = 210 байт = 1024 байт
1 мегабайт = 1 Мб = 210 Кб = 1024 Кб
1 гигабайт = 1 Гб = 210 Мб = 1024 Мб
— Попробуйте перевести результат задачи, в более крупные единицы измерения:
60000 байт • 58,59375 Кб
60000 байт • 0,057 Мб
IV. Закрепление изученного.
Задачник-практикум № 1. С. 19 № 19, 20, 22, 23, 25.
V. Подведение итогов.
VI. Домашнее задание.
Задачник-практикум № 1. с. 20 № 21, 24, 26.
Мощность алфавита в информатике
Описание термина
Понятие мощности алфавита находится в основании изучения информатики. Алфавитом принято называть набор многочисленных символов. Сумма всех их в определённом языке и есть алфавитная мощность. Иными словами, это количество всех символов, входящих в конкретно взятый язык. Сюда входят не только буквы, но и прочие обозначения, в частности:
Это определение считается обобщённым и не принимает во внимание вычисления информационной составляющей сообщения. Она может содержать в себе числа, знаки препинания и прочее. В этом случае прибегают к использованию другого способа. Его суть основывается на том, что любая буква, цифра или знак обладают собственным информационным объемом данных. Компьютер работает с этим информационным кодом и распознает то, что было написано.
Основным постулатом в информатике является тот факт, что устройство разбирает введённую информацию исключительно в двоичном коде в форме нуля и единицы. В итоге получается, что абсолютно любой символ алфавита может быть успешно закодирован при помощи соответствующего подбора этих двух цифровых символов. Самая маленькая последовательность, применяемая при обозначении какой-либо цифры, буквы или другого знака, состоит из двух элементов.
Информационная масса отдельно взятого символа обычно изображается в форме информационной стандартной измерительной единицы, которая называется «бит». Восемь битов становятся равны одному байту.
Отображение символов в двоичном коде
Алфавитная мощность может быть использована на практике только при наличии двоичного кода. В качестве примера можно использовать упрощённый алфавит, состоящий всего из четырёх символов. В этом случае разрядность их и информационное представление описываются следующим образом:
Из этого списка можно сделать вывод о том, что если алфавитная мощность равняется 4, то масса отдельного единичного символа будет составлять 2 бита. Если же есть алфавит, состоящий из 8 символов, то при подборе двоичного трёхзначного кода для него комбинационное количество будет следующим:
Иными словами, если алфавитная мощность равна 8, то вес отдельно взятого символа для двоичного трёхзначного кода составит 3 бита.
Вычисление мощности алфавита
Эта формула была изобретена американским инженером Ральфом Хартли более сотни лет тому назад. Она применяется для работы с равновероятными событиями и используется для определения мощности конкретного буквенного набора, которая обозначается буквой N (информационная масса или объём). n означает численность бит в словесной единице, иными словами, количество знаков внутри двоичного кода. Так, если n равен 1, то N тоже равен 1, при n = 2 N = 4, при n = 3 N = 8, при n = 4 N = 16.
Чтобы сформулировать теорию о численности информации в набранном словосочетании, пользуются формулой I=K*i. В этом случае К обозначает численность всех символов в предложении, а i — это информационная масса символа.
При ответе на вопрос, как найти мощность алфавита, нужно сказать, что в русском языке 33 буквы, поэтому это можно выразить как N = 33. Для сравнения, аналогичный показатель в английском, немецком и французском языках равняется 26, в испанском — 27. Венгерский язык, например, является 40-символьным.
Существует также и клавиатурный язык, куда входят не только буквы, но и дополнительные знаки. Так, в русском языке есть ещё 10 цифр и 11 символов, а также пробел и пара скобок. Их мощность прибавляется к аналогичному буквенному показателю, и на выходе получается N = 33+10+11+1+2=57. В некоторых случаях букву «ё» не выделяют в качестве отдельного самостоятельного символа, и в таком случае полная мощность русского алфавита становится равна 56.
Определение информационного объёма в тексте
Почти всегда при наборе текста на компьютерах и других электронных устройствах приходится сталкиваться с написанием различных символов. К ним следует отнести:
По всем расчётам получается, что мощность компьютерного алфавита составляет 256 различных символов и вариантов. В соответствии с формулой Хартли, N = 256, а i — масса любого из значков в клавиатурном алфавите соответствует одному байту, или восьми битам.
Размер любой напечатанной фразы может быть вычислен по формуле V=K ⋅ log2N. В этом случае N обозначает количество всех символов в алфавите, а K — это численность знаков непосредственно в напечатанной фразе. Так, например, имеется произвольный текст объёмом в 25 листов. На каждом из них расположено по 45 строчек текста, содержащих по 58 символов.
Исходя из этого, на любой отдельной странице будет 45*58 = 2610 байт информации. В целом же по всему тексту этот объём будет равен 2610*25 = 65250 байт. Для обозначения мощности алфавита в информатике общепринятым вариантом является буква N из формулы Хартли. Именно ее чаще всего указывают в большинстве учебников и профессиональной литературе.
В кодовой таблице ASCII используют восьмибитную кодировку текстовых сообщений. Она позволяет полностью вместить основной набор символов кириллического и латинского алфавитов как в строчном, так и в прописном вариантах. Также с её помощью можно отобразить знаки препинания, цифры и прочие базовые знаки. Часто пользователям приходится иметь дело с более крупными объёмами, состоящими из триллионов байтов.
Для удобства их всегда переводят в увеличенные величины — кило-, мега-, гигабайты и прочее. Для их упрощённого обозначения используются специальные сокращения: Кб, Мб, Гб и так далее. 1 Кб равняется 1024 байтам (2 байта в десятой степени), 1 Мб составляет 1024 Кб (2 Кб в десятой степени) и так далее. Исходя из этого, 65250 байт будут составлять 63,72 килобайта.
Поскольку один отдельный символ состоит из 8 битов, то устанавливать их кодировку целиком не представляется возможным. Вместо этого предпочтительнее образовать кодировку трёхбитовых комбинаций. Расчёт этого действия проводится по формуле Хартли, где n-ная степень будет равняться трём. В результате получается N, равная 8.
При определении мощности чаще всего используют алфавитный подход. Он говорит о том, что объём информации, заложенной в тексте, зависит исключительно от мощности самого алфавита и размера сообщения (то есть количества символов, содержащихся в нём). Этот показатель не имеет никакой связи со смысловым наполнением для человека.
Примеры расчёта мощности
От пользователей или обучающихся в задачах часто требуют научиться определять информационный объём какого-либо сообщения, приняв информационный вес символа за один байт. Так, в отрывке из поэмы Н. Н. Некрасова «Крестьянские дети»:
Я из лесу вышел; был сильный мороз»
будет 67 символов вместе с пробелами, то есть, в соответствии с условиями задания, 67 байт. Их количество умножают на 8 (количество битов в байте), и на выходе получается 536 битов.
Таким образом, зная в теории суть мощности, можно без проблем определять информационный объем различных сообщений.