Перпендикулярность
Содержание
На плоскости
Перпендикулярные прямые
Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.
В аналитическом выражении прямые, заданные линейными функциями 




Для обозначения перпендикулярности имеется общепринятый символ: 
Построение перпендикуляра
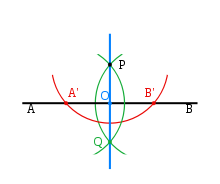
Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А’ и В’.
Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A’ и В’ соответственно, проходящими через точку Р. Кроме точки Р есть ещё одна точка пересечения этих полуокружностей, назовём её Q.
Шаг 3: (синий) Соединяем точки Р и Q. PQ и есть перпендикуляр к прямой АВ.
Координаты точки основания перпендикуляра к прямой
A(xa,ya) и B(xb,yb) — прямая, O(xo,yo) — основание перпендикуляра, опущенного из точки P(xp,yp).
Если xa = xb (вертикаль), то xo = xa и yo = yp. Если ya = yb (горизонталь), то xo = xp и yo = ya.
Во всех остальных случаях
xo = (xa*(yb-ya)^2 + xp*(xb-xa)^2 + (xb-xa) * (yb-ya) * (yp-ya)) / ((yb-ya)^2+(xb-xa)^2); yo = (yb-ya)*(xo-xa)/(xb-xa)+ya.
В трёхмерном пространстве
Перпендикулярные прямые
Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим прямым, лежащим в одной плоскости и перпендикулярным в ней.
Перпендикулярность прямой и плоскости
Определение: Прямая называется перпендикулярной плоскости, если она перпендикулярна всем прямым лежащим в этой плоскости.
Признак: Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.
Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Перпендикулярные плоскости
Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.
В многомерных пространствах
Перпендикулярность плоскостей в 4-мерном пространстве
Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.
Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.
В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).
Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно 
Перпендикулярность прямой и гиперплоскости
Пусть задано n-мерное евклидово пространство 







Прямая l называется перпендикулярной гиперплоскости 


Как пишется перпендикулярно знак
Углы бывают острые, прямые и тупые.
Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.
Два угла с одной общей стороной называются смежными.
На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.
Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°
При пересечении двух прямых образуются четыре угла:
Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.
∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4
То же справедливо и для ∡1 и ∡3.
Прямые, пересекающиеся под прямым углом, называются перпендикулярными.
∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.
Перпендикулярность прямых принято обозначать так: a⟂b
Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!
Теорема о перпендикулярных прямых
Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.
Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.
Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.
Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.
Свойство перпендикулярных прямых
Две прямые, перпендикулярные третьей, не пересекаются.
Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.
У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Интересное по рубрике
Найдите необходимую статью по тегам
Подпишитесь на нашу рассылку
Мы в инстаграм
Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Перпендикулярные прямые, условие перпендикулярности прямых.
В этой статье подробно рассмотрим перпендикулярные прямые на плоскости и в трехмерном пространстве. Начнем с определения перпендикулярных прямых, покажем обозначения и приведем примеры. После этого приведем необходимое и достаточное условие перпендикулярности двух прямых и детально разберем решения характерных задач.
Навигация по странице.
Перпендикулярные прямые – основные сведения.
Угол между пересекающимися прямыми на плоскости и в трехмерном пространстве может быть равен девяноста градусам. В этом случае говорят, что прямые пересекаются под прямым углом, а прямые называют перпендикулярными. Если угол между скрещивающимися прямыми в трехмерном пространстве равен 
Отметим, что фразы «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» равноправны. Поэтому можно слышать, что перпендикулярные прямые называют взаимно перпендикулярными.
Учитывая все сказанное, дадим общее определение перпендикулярных прямых.
Две прямые называются перпендикулярными, если угол между ними равен 
Для обозначения перпендикулярных прямых используют знак перпендикулярности вида «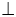
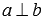
Перпендикулярные прямые фигурируют чуть ли не в каждой геометрической задаче. Иногда перпендикулярность прямых известна из условия, а в других случаях перпендикулярность прямых приходится доказывать. Для доказательства перпендикулярности двух прямых достаточно показать, используя любые геометрические методы, что угол между прямыми равен девяноста градусам.
А как ответить на вопрос «перпендикулярны ли прямые», если известны уравнения, задающие эти прямые в прямоугольной системе координат на плоскости или в трехмерном пространстве?
Для этого следует воспользоваться необходимым и достаточным условием перпендикулярности двух прямых. Сформулируем его в виде теоремы.
Доказательство этого условия перпендикулярности прямых основано на определении направляющего вектора прямой и на определении перпендикулярных прямых.
Итак, необходимое и достаточное условие перпендикулярности прямых a и b в прямоугольной системе координат Oxy на плоскости имеет вид 

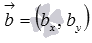
Это условие удобно использовать, когда легко находятся координаты направляющих векторов прямых, а также когда прямым a и b соответствуют канонические уравнения прямой на плоскости или параметрические уравнения прямой на плоскости.
да, прямые перпендикулярны.
Являются ли прямые 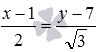

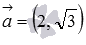
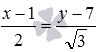



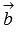

нет, прямые не перпендикулярны.
Аналогично, необходимое и достаточное условие перпендикулярности прямых a и b в прямоугольной системе координат Oxyz в трехмерном пространстве имеет вид 
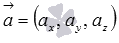

Перпендикулярны ли прямые, заданные в прямоугольной системе координат Oxyz в трехмерном пространстве уравнениями 
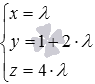
Числа, стоящие в знаменателях канонических уравнений прямой в пространстве, являются соответствующими координатами направляющего вектора прямой. А координатами направляющего вектора прямой, которая задана параметрическими уравнениями прямой в пространстве, являются коэффициенты при параметре. Таким образом, 
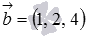

Для проверки перпендикулярности двух прямых на плоскости существуют другие необходимые и достаточные условия перпендикулярности.
Озвученное условие перпендикулярности прямых удобно использовать, если по заданным уравнениям прямых легко находятся координаты нормальных векторов прямых. Этому утверждению отвечает общее уравнение прямой вида 
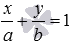
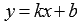
Убедитесь, что прямые 
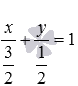
По заданным уравнениям прямых легко найти координаты нормальных векторов этих прямых. 

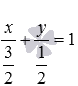
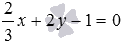

Векторы 

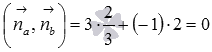
В частности, если прямую a на плоскости определяет уравнение прямой с угловым коэффициентом вида 

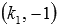


Перпендикулярны ли прямые 

Угловой коэффициент прямой 




заданные прямые перпендикулярны.
Можно озвучить еще одно условие перпендикулярности прямых на плоскости.
Для перпендикулярности прямых a и b на плоскости необходимо и достаточно, чтобы направляющий вектор одной прямой и нормальный вектор второй прямой были коллинеарны.
Этим условием, очевидно, удобно пользоваться, когда легко находятся координаты направляющего вектора одной прямой и координаты нормального вектора второй прямой, то есть, когда одна прямая задана каноническим уравнением или параметрическими уравнениями прямой на плоскости, а вторая – или общим уравнением прямой, или уравнением прямой в отрезках, или уравнением прямой с угловым коэффициентом.
Являются ли прямые 
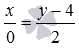


.jpg)

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)





