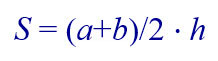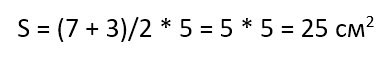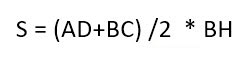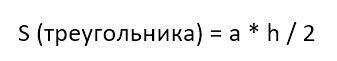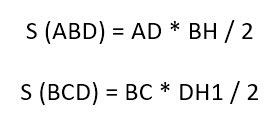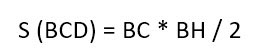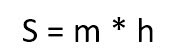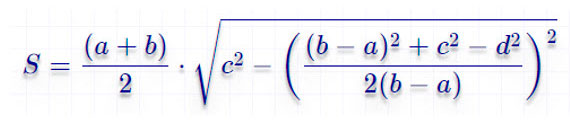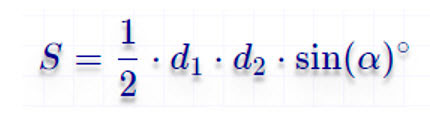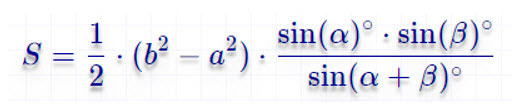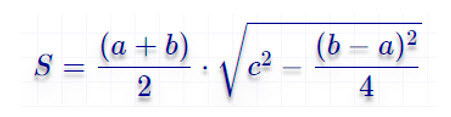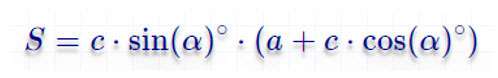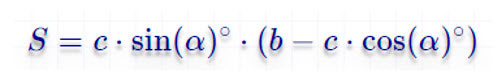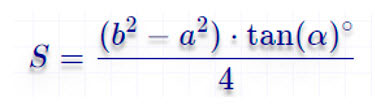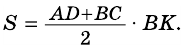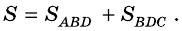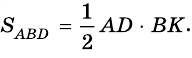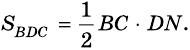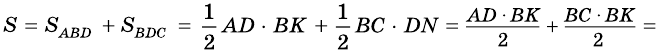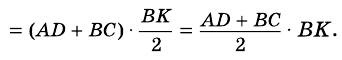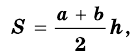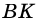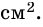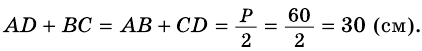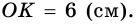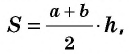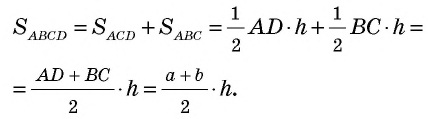Площадь трапеции
Трапеция — геометрическая фигура, представляющая собой выпуклый четырёхугольник, у которого основания параллельны, а боковые стороны – нет. Средняя линия трапеции — отрезок, соединяющий середины боковых сторон. Калькуляторы для нахождения площади трапеции находятся внизу страницы.
Формулы нахождения площади
Существует несколько базовых способов нахождения площади трапеции, в зависимости от того, какие исходные данные известны.
Через основания и высоту
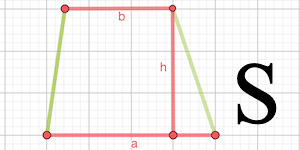
Площади трапеции можно определить, если известны значения длин ее оснований и высоты:
где a и b – основания, h – высота.
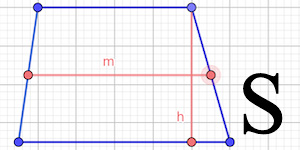
Через среднюю линию и высоту
где m – средняя линия, h – высота.
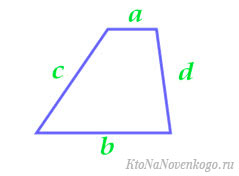
Через четыре стороны
Пусть a – верхнее основание, b – нижнее, c и d – боковые стороны трапеции. Тогда формула для нахождения площади:
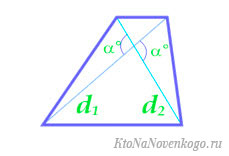
По диагоналям и углу между ними
где d1 и d2 – диагонали трапеции, α – угол между ними.
Через вписанную в равнобедренную трапецию окружность
где r – радиус окружности, α – угол при основании трапеции.
Расчет площади трапеции через высоту, верхнее и нижнее основание
Расчет площади трапеции через значения ее высоты и средней линии.
Как найти площадь трапеции
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, как посчитать площадь трапеции. Эту тему подробно изучают в школе в 8-м классе.
Но в классической программе учителя дают далеко не все формулы, с помощью которых можно вычислить нужное значение. И ограничиваются, как правило, одной или двумя.
Мы же дадим максимально развернутый ответ на этот вопрос. Ведь трапеция – это весьма примечательная и сложная фигура в геометрии. А соответственно, и формулы для вычисления ее площади отличаются определенной сложностью и громоздкостью.
Тут нет банальных «перемножить длины сторон», как у площади прямоугольника. Все гораздо мудреней.
Что такое трапеция
Но для начала будет нелишним напомнить, что из себя представляет трапеция.
Трапеция – это геометрическая фигура, которая является четырехугольником, и у которой две противоположные стороны параллельны.
Последнее утверждение очень важное. ТОЛЬКО ДВЕ противоположные стороны параллельны у трапеции. Ведь если бы обе пары лежали на параллельных прямых, то это был бы уже параллелограмм.
Вот так выглядит трапеция:
А вот так параллелограмм:
Кстати, именно по этому принципу древний математик Евклид и разделил все четырехугольники на две большие категории.
Именно он впервые описал разные геометрические фигуры, в том числе трапеции и параллелограммы. И все свои соображения подробно изложил в книге «Начала», которая датируется 300 годом до нашей эры.
Что такое площадь
Раз уж мы решили вычислять эту величину, напомним, что она обозначает.
Площадь – это численное значение геометрической фигуры, нарисованной в двухмерном (плоском) пространстве. А проще говоря, это пространство, которое ограничено границами фигуры, и находится как бы внутри нее.
В нашем случае площадь трапеции – это область, закрашенная синим цветом:
Кстати, в древности вместо термина «площадь» говорили «квадратура». Считалось, что любую фигуру можно разбить на равные квадраты со стороной «один». Частично это понятие докатилось и до наших дней.
Ведь именно в «квадратных метрах» мы измеряем площадь комнаты/квартиры/дачи/офиса. И в «квадратных километрах» частенько озвучивают площадь какой-то территории. Например, когда в телевизионных новостях говорят о масштабах лесных пожаров или наводнений.
Главная формула для вычисления площади трапеции
Та формула, которую изучают в школе, основана на вычислении площади трапеции по длине ее оснований и высоте.
Основания трапеции – это стороны, которые лежат на параллельных прямых. Другая пара сторон называется боковыми.
Высота – это отрезок, проведенный из вершины любого угла к противоположному основанию под углом 90 градусов.
То есть мы имеем вот такие исходные данные:
Здесь «a» и «b» являются основаниями трапеции, а «h» — высотой.
И тогда формула для вычисления площади трапеции выглядит вот так:
Например, если длины сторон и высота равны:
то площадь такой трапеции будет равна:
Опять же заметьте, если стороны и высота у трапеции обозначались в сантиметрах, то площадь будет измеряться в квадратных сантиметрах (то самое понятие «квадратуры», о котором мы писали выше).
То же самое – миллиметры/квадратные миллиметры, метры/квадратные метры, километры/квадратные километры и так далее.
Доказательство теоремы о площади трапеции
Любая формула в геометрии требует доказательства. И в нашем случае, формулы вычисления площади трапеции также доказывают во время уроков.
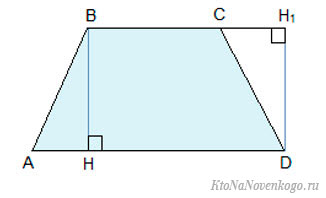
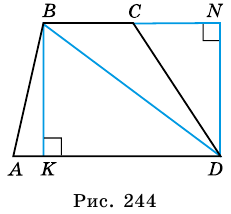
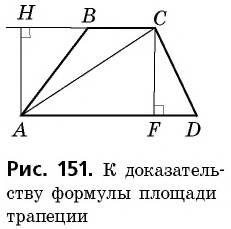
Возьмем для примера трапецию:
В ней AD и BC – основания, BH – высота. Нам надо доказать, что:
Доказательство строится на том, что если провести диагональ BD, то она разделит нашу трапецию на два треугольника. Это будут треугольники ABD и BCD.
И чтобы получить площадь нашей трапеции, нужно посчитать отдельно площади этих треугольников и сложить их.
А как вычислять площадь треугольника, мы уже знаем (или должны знать, согласно школьному курсу). Надо перемножить длину его основания и высоту и поделить на два.
У треугольника ABD высота – это BH. А у треугольника BCD в силу его выпуклости нам пришлось продлить зрительно основание BC, чтобы получить высоту DH1.
Но в случае с трапецией высоты равны, то есть BH = DH1. И тогда формулу площади для второго треугольника можно заменить на:
И наконец, с учетом всего вышесказанного начинаем вычислять площадь нашей трапеции. Она равна:
Как часто говориться на уроках геометрии – что и требовалось доказать!
Извиняемся за столь подробное описание доказательства. Но, во-первых, это требуется в рамках школьной программы. А во-вторых, всегда ведь интересно докопаться до самой сути и понять, как и почему именно так что-то устроено.
Как еще можно найти площадь трапеции (другие формулы)
На этот раз мы уже не будем приводить подробные доказательства каждой из формул. Иначе это займет слишком много времени и места. Просто поверьте, все они правильные и по ним можно вычислить площадь трапеции.
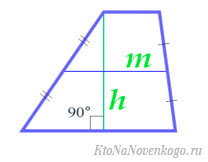
По высоте и средней линии
Средняя линия – это та, которая делит боковые стороны трапеции на две равные части. Формула площади выглядит совсем просто:
По четырем сторонам
Тут формула гораздо сложнее:
Площадь трапеции через диагонали
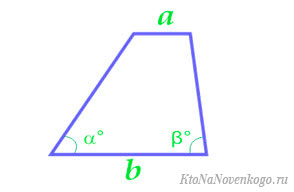
По основанию и углам при нем
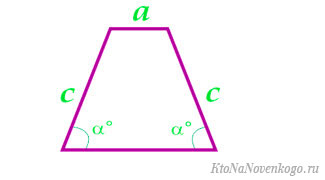
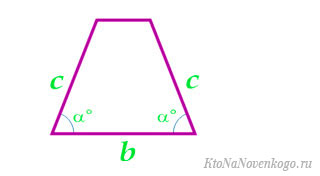
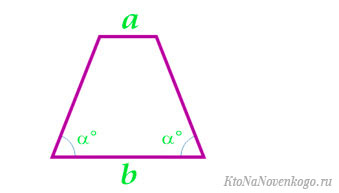
Формулы площади для равнобедренной трапеции
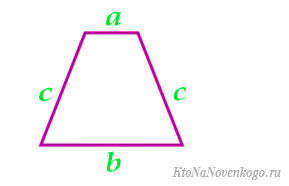
Равнобедренная трапеция – та, у которой боковые стороны равны. А соответственно, они еще и соприкасаются с основаниями под одинаковыми углами.
Это частный случай, и для него верны все перечисленные формулы. Но с учетом равенства сторон и углов формулы заметно упрощаются.
По четырем сторонам
По малому основанию, боковой стороне и углу у большого основания
По большому основанию, углу при нем и боковой стороне
По основаниям и углам
Как видите, формулы громоздкие и весьма сложные сами по себе. Без калькулятора здесь точно не обойтись. С другой стороны, они крайне редко применяются. И служат скорее дополнительными средствами.
Вот и все, что мы хотели рассказать о том, как вычислять площадь трапеции.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Теперь любой школьник сможет блеснуть знаниями перед учителем, продемонстрировав несколько способов нахождения площади трапеции. Я уже далеко не школьник, но тоже было интересно.
Теорема (о площади трапеции). Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Доказательство:
Пусть
Докажем, что площадь 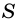
1) Диагональ 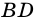
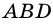
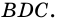
2) 
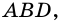
3) Проведем в трапеции высоту 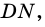
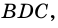
4) 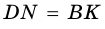
В общем виде формулу площади 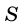
где 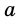
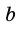
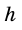
Следствие. Площадь трапеции равна произведению ее средней линии на высоту.
Пример:
В трапеции 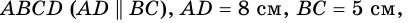
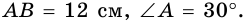
Решение:
1) Проведем в трапеции 
(рис. 245). В 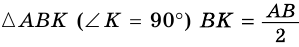
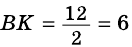
2)
Ответ. 39
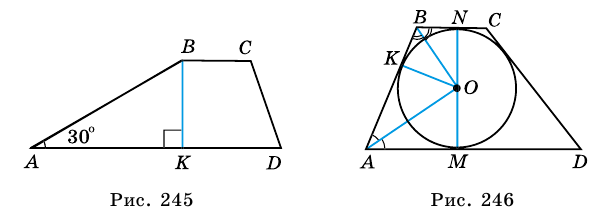
Пример:
Периметр трапеции 60 см, а одна из боковых сторон точкой касания вписанной окружности делится на отрезки 9 см и 4 см. Найдите площадь трапеции.
Решение:
1) Так как трапеция является описанной около окружности (рис. 246), то
3) Точка 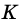
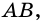
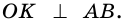
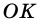
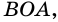
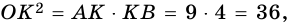
4) 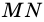
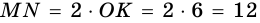
5) Следовательно,
Ответ. 180
Площадь трапеции
Часто для вычисления площади некоторого многоугольника его разбивают на несколько треугольников и находят искомую площадь как сумму площадей этих треугольников. Именно такой подход можно применить для вывода формулы площади трапеции.
Теорема (формула площади трапеции) Площадь трапеции равна произведению полусуммы ее оснований на высоту:
где 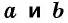
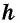
Пусть дана трапеция 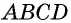
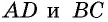
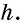
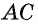
Проведем высоты этих треугольников 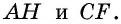
Следствие
Площадь трапеции равна произведению средней линии на высоту.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Трапеция
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a – h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a – c· cos α – d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
| с = | h | d = | h |
| sin α | sin β |
Как найти площадь трапеции через четыре стороны
Отнимите от большего основания меньшее.
Найдите квадрат полученного числа.
Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.
Поделите полученное число на удвоенную разность оснований.
Найдите квадрат результата и отнимите его от квадрата боковой стороны.
Найдите корень из полученного числа.
Умножьте результат на половину от суммы оснований.
Средняя линия трапеции
Средняя линия – отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
2. Формула определения длины средней линии через площадь и высоту:
| m = | S |
| h |
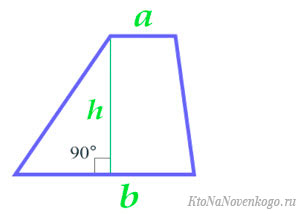
Через длины оснований и высоту
Чему равна площадь трапеции если известны основания a и b, а также высота h?
Формула
Пример
Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:
S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²
Площадь трапеции через перпендикулярные диагонали
Как вычислить площадь равнобедренной трапеции через четыре стороны
Отнимите от большего основания трапеции меньшее и поделите результат на два.
Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.
Найдите корень из результата.
Умножьте полученное число на сумму оснований и поделите на два.
Таблица с формулами площади трапеции
В зависимости от известных исходных данных и вида трапеции, площадь трапеции можно вычислить по различным формулам.
| эскиз | формула | ||
| Площадь для всех видов трапеции | |||
| 1 | высота и два основания |  | |
| 2 | высота и средняя линия |  | |
| 3 | четыре стороны |  | |
| 4 | диагонали и угол между ними |  | |
| 5 | основания и углы при одном из оснований |  | |
| Площадь равнобедренной трапеции | |||
| 6 | стороны |  | |
| 7 | основание, боковые стороны и угол при основании |  | |
| 8 | основание, боковые стороны и угол при основании |  | |
| 9 | основания и углы при одном из оснований |  | |
| 10 | диагонали и угол между ними |  | |
| 11 | средняя линия, боковые стороны и углы между основанием и боковыми сторонами |  | |
| 12 | радиус вписанной окружности и угол при основании |  | |
| 13 | основания и радиус вписанной окружности |  | |
| 14 | основания и углы при одном из оснований |  | |
| 15 | основания и боковые стороны |  | |
| 16 | основания и средняя линия |  | |
Найти площадь равнобедренной трапеции, зная радиус вписанной окружности и угол
Через среднюю линию, боковую сторону и угол при основании
Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Пусть a и b основания трапеции. доказать что отрезок, соединяющий середины её диагоналей равен 1/2 * | а – б|?
Возьмем трапецию ABCD
Определим точку М как середину диагонали АС, точку N как середину диагонали BD. Тогда средняя линия трапеции KF будет проходить через точки M и N.
Вспомним свойство средней линии трапеции: средняя линия трапеции является параллельной основаниям и равняется полусумме их длин.
Рассмотрим треугольник ACD:
Рассмотрим треугольник BCD
Выразим MN через отрезки MF и NF:
Подставим в формулу значения отрезков MF и NF: