Пустое множество
Пусто́е мно́жество (в математике) — множество, не содержащее ни одного элемента. Из аксиомы объёмности следует, что есть только одно множество, обладающее таким свойством. Пустое множество является своим (тривиальным) подмножеством, но не является своим элементом.
Пустое множество является конечным множеством и имеет наименьшую мощность среди всех множеств. Пустое множество — единственное множество, для которого класс множеств, равномощных ему, состоит из единственного элемента (самого́ пустого множества). Также, пустое множество — единственное множество, имеющее ровно 1 подмножество (само себя), и единственное множество, равномощное любому своему подмножеству.
Пустое множество тривиальным образом является разрешимым (а значит, перечислимым и арифметическим), транзитивным (англ.) и вполне упорядоченным множеством (для любого отношения порядка). Пустое множество является наименьшим порядковым числом и наименьшим кардинальным числом. В топологии, пустое множество является одновременно замкнутым и открытым множеством.
-цепочка, начинающаяся с произвольного множества, каждый последующий член которой является элементом предыдущего, всегда через конечное число шагов завершается пустым множеством (см. аксиому регулярности). Таким образом, пустое множество является «строительным кирпичиком», из которого строятся все остальные множества.
В некоторых формулировках теории множеств существование пустого множества постулируется (см. аксиому пустого множества), в других — доказывается.
Содержание
Обозначения пустого множества
Обычно пустое множество обозначают одним из следующих символов: 
, 
и 
.
Реже пустое множество обозначают одним из следующих символов: 
и 
.
В Юникоде имеется специальный символ «пустое множество» (U+2205, ∅ ).
Символы и введены в употребление группой Бурбаки (в частности, Андре Вейлем) в 1939 году.
Свойства пустого множества
См. также
Ссылки
Полезное
Смотреть что такое «Пустое множество» в других словарях:
пустое множество — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN empty set … Справочник технического переводчика
пустое множество — понятие теории множеств; пустое множество множество, не содержащее ни одного элемента; обозначается ø или 0. Понятие пустое множество (подобно понятию «нуль») возникает из потребности, чтобы результат всякой операции над множествами был также… … Энциклопедический словарь
пустое множество — tuščioji aibė statusas T sritis automatika atitikmenys: angl. empty set vok. Leerensemble, n rus. пустое множество, n pranc. ensemble vide, m … Automatikos terminų žodynas
Пустое множество — (математическое) «множество», не содержащее ни одного элемента. Понятие «П. м.» (подобно понятию «нуль»; возникает из потребности, чтобы результат всякой операции над множествами был также множеством (см. Множеств теория). Источником… … Большая советская энциклопедия
ПУСТОЕ МНОЖЕСТВО — понятие теории множеств; П. м. множество, не содержащее ни одного элемента; обозначается 0. Понятие П. м. (подобно понятию нуль ) возникает из потребности, чтобы результат всякой операции над множествами был также множеством … Естествознание. Энциклопедический словарь
Множество — У этого термина существуют и другие значения, см. Множество (значения). Запрос «Целое» перенаправляется сюда; о типе данных в программировании см. Целое (тип данных). Множество одно из ключевых понятий математики, в частности, теории… … Википедия
Множество (тип данных) — У этого термина существуют и другие значения, см. Множество (значения). Множество тип и структура данных в информатике, является реализацией математического объекта множество. Данные типа множество позволяют хранить ограниченное число значений… … Википедия
Множество (математика) — Множество один из ключевых объектов математики, в частности, теории множеств. «Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли» (Г. Кантор). Это не является в полном… … Википедия
Непустое множество
Пустым множеством в математике называется множество, не содержащее ни одного элемента.
В одних теориях множеств существование [по меньшей мере одного] пустого множества провозглашается (см. аксиому пустого множества), в других — доказывается. Во всех теориях множеств единственность пустого множества доказывается (см. аксиому объёмности).
Содержание
Обозначения пустого множества
Обычно пустое множество обозначают одним из следующих символов: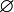 
, 
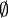
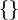
и 
.
Реже пустое множество обозначают одним из следующих символов: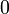 
и 
В Юникоде имеется специальный символ «пустое множество» (U+2205, ∅ ).
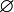
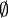
Символы и введены в употребление группой Бурбаки (в частности, Андре Вейлем) в 1939 году.
Символ 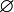идентичен букве Ø в Датско-норвежском алфавите. [1]
Свойства пустого множества
См. также
Ссылки
Полезное
Смотреть что такое «Непустое множество» в других словарях:
Множество — У этого термина существуют и другие значения, см. Множество (значения). Запрос «Целое» перенаправляется сюда; о типе данных в программировании см. Целое (тип данных). Множество одно из ключевых понятий математики, в частности, теории… … Википедия
ЧАСТИЧНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО — непустое множество, на к ром зафиксирован нек рый порядок. Ч. у. м. является примером модели. Примеры Ч. у. м.: 1) множество натуральных чисел с обычным порядком; 2) множество натуральных чисел, где означает, что аделит b; 3) множество всех… … Математическая энциклопедия
Направленное множество — В математике, направленным множеством называется непустое множество A с заданным на нем рефлексивным транзитивным отношением ≤ (т. е. предпорядком), обладающее дополнительным свойством: для любых двух элементов из A найдется элемент из A… … Википедия
ПРОЕКТИВНОЕ МНОЖЕСТВО — множество, к рое может быть получено из борелевских множеств повторным применением операций проектирования и перехода к дополнению. П. м. классифицируются по классам, образующим проективную иерархию. Пусть I=ww бэровское пространство… … Математическая энциклопедия
Частично упорядоченное множество — У этого термина существуют и другие значения, см. Упорядоченное множество. Подмножества
Нечёткое множество — Эту страницу предлагается объединить с Теория нечётких множеств … Википедия
Нечеткое множество — Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество понятие, введённое Лотфи Заде в 1965 г. в статье «Fuzzy Sets» (нечёткие множества) в журнале Information and Control [1]. Л. Заде расширил классическое канторовское понятие… … Википедия
Пушистое множество — Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество понятие, введённое Лотфи Заде в 1965 г. в статье «Fuzzy Sets» (нечёткие множества) в журнале Information and Control [1]. Л. Заде расширил классическое канторовское понятие… … Википедия
ПУСТОЕ МНОЖЕСТВО
— множество, не содержащее элементов. Обозначения: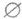 
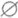
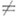
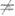
, Л. Иначе, 
=<х: х 
х>, при этом вместо х 
х в этом определении можно было бы использовать любое всегда ложное утверждение. П. м. является подмножеством любого множества. М. И. Войцеховский.
Смотреть что такое «ПУСТОЕ МНОЖЕСТВО» в других словарях:
пустое множество — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN empty set … Справочник технического переводчика
Пустое множество — Обозначение пустого множества Пустое множество (в математике) множество, не содержащее ни одного элемента. Из аксиомы объёмности следует, что есть только одно множество, обладающее таким свойс … Википедия
пустое множество — понятие теории множеств; пустое множество множество, не содержащее ни одного элемента; обозначается ø или 0. Понятие пустое множество (подобно понятию «нуль») возникает из потребности, чтобы результат всякой операции над множествами был также… … Энциклопедический словарь
пустое множество — tuščioji aibė statusas T sritis automatika atitikmenys: angl. empty set vok. Leerensemble, n rus. пустое множество, n pranc. ensemble vide, m … Automatikos terminų žodynas
Пустое множество — (математическое) «множество», не содержащее ни одного элемента. Понятие «П. м.» (подобно понятию «нуль»; возникает из потребности, чтобы результат всякой операции над множествами был также множеством (см. Множеств теория). Источником… … Большая советская энциклопедия
ПУСТОЕ МНОЖЕСТВО — понятие теории множеств; П. м. множество, не содержащее ни одного элемента; обозначается 0. Понятие П. м. (подобно понятию нуль ) возникает из потребности, чтобы результат всякой операции над множествами был также множеством … Естествознание. Энциклопедический словарь
Множество — У этого термина существуют и другие значения, см. Множество (значения). Запрос «Целое» перенаправляется сюда; о типе данных в программировании см. Целое (тип данных). Множество одно из ключевых понятий математики, в частности, теории… … Википедия
Множество (тип данных) — У этого термина существуют и другие значения, см. Множество (значения). Множество тип и структура данных в информатике, является реализацией математического объекта множество. Данные типа множество позволяют хранить ограниченное число значений… … Википедия
Множество (математика) — Множество один из ключевых объектов математики, в частности, теории множеств. «Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли» (Г. Кантор). Это не является в полном… … Википедия
Что такое множество в математике?
Понятие множества в математике — одно из фундаментальных понятий. Без его хотя бы поверхностного изучения не стоит начинать и изучение более сложных разделов математики. Теорию множеств на доступном уровне преподают уже в средней школе. Предлагаю Вам их еще раз пройти вместе со мной.
Что такое множество?
Строго говоря, дать определение «множества» нельзя. С точки зрения науки логики такие определения в любом случае противоречивы. Подойдем с другой стороны и будем считать, что мы УЖЕ работаем с множеством произвольной природы, обозначим его X, которое состоит из элементов x (буквы не принципиальны).
x — элемент множества X
В данном случае нам неинтересна природа множеств, нам важен только вопрос включения/не включения отдельного элемента в это множество, т.е. максимально абстрактное представление. Попытаться определить, что такое множество можно следующим образом. Пусть X — известное нам множество, тогда мы можем определить множество Y, состоящее из таких элементов x, принадлежащих X, которые удовлетворяют некоторому свойству.
Да, получается, что мы не можем дать определение множеству, если до этого не согласимся, что имеем с ним дело в другом месте. Классический парадокс Мюнхгаузена.
Приведем простой пример. Я думаю не подвергается сомнению, что существуют натуральные числа: 1,2,3 и т.д., другими словами, имеется множество натуральных чисел (обозначают N). Выделим из него, например, четные числа, обозначим их N2, N4 и т.д.. Теперь мы можем утверждать, что множество четных чисел S (буква не принципиальна) состоит из чиселN2, N4 и т.д, удовлетворяющих свойству четности и принадлежащих N.
n mod 2 — операция, вычисляющая остаток от деления на 2. Например, 5 mod 2 = 1, 4 mod 2 = 0.
Таким образом, мы только что задали множество четных чисел, выделив его из множества натуральных чисел. В теории множеств говорят, что мы выделили подмножество (часть) S в множестве N. Обозначается вот так:
Читается так: S является подмножеством N, что эквивалентно тому, что для любого элемента s его принадлежность множеству S определяет принадлежность к множеству N (или принадлежность к множеству N следует из принадлежности к множеству S).
Знак включения между S и N строгий. Он означает, что множества N и S не равны. Действительно в нашем примере во множестве N есть еще и множество нечетных чисел. Нестрогий знак обозначается так:
Здесь мы определили. что множество S является подмножеством самого себя и содержит те же элементы. Такое свойство называется рефлексивностью.
Понятие пустого множества
На самом деле пустое множество — множество, не содержащее ни одного элемента — одно из самых важных понятий всей теории. Обозначается оно следующим образом:
Чем же примечательно пустое множество? Во-первых, это единственное множество которое является подмножествами любых множеств. Во-вторых, пустое множество является подмножеством себя, но не является своим элементом (вспомните определение). В-третьих, в топологии пустое множество одновременно является открытым и замкнутым (крючок на будущее, пока без пояснения).
Парочка небольших примеров на закрепление:
На этом закончим. В этой статье мы рассмотрели как определяется множество, что такое подмножество и пустое множество, каковы их свойства (но пока не все). Рассмотрели несколько примеров для понимания.
В следующем материале мы рассмотрим основные операции над множествами.
Пустое множество
Смотреть что такое «Пустое множество» в других словарях:
пустое множество — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN empty set … Справочник технического переводчика
Пустое множество — Обозначение пустого множества Пустое множество (в математике) множество, не содержащее ни одного элемента. Из аксиомы объёмности следует, что есть только одно множество, обладающее таким свойс … Википедия
пустое множество — понятие теории множеств; пустое множество множество, не содержащее ни одного элемента; обозначается ø или 0. Понятие пустое множество (подобно понятию «нуль») возникает из потребности, чтобы результат всякой операции над множествами был также… … Энциклопедический словарь
пустое множество — tuščioji aibė statusas T sritis automatika atitikmenys: angl. empty set vok. Leerensemble, n rus. пустое множество, n pranc. ensemble vide, m … Automatikos terminų žodynas
ПУСТОЕ МНОЖЕСТВО — понятие теории множеств; П. м. множество, не содержащее ни одного элемента; обозначается 0. Понятие П. м. (подобно понятию нуль ) возникает из потребности, чтобы результат всякой операции над множествами был также множеством … Естествознание. Энциклопедический словарь
Множество — У этого термина существуют и другие значения, см. Множество (значения). Запрос «Целое» перенаправляется сюда; о типе данных в программировании см. Целое (тип данных). Множество одно из ключевых понятий математики, в частности, теории… … Википедия
Множество (тип данных) — У этого термина существуют и другие значения, см. Множество (значения). Множество тип и структура данных в информатике, является реализацией математического объекта множество. Данные типа множество позволяют хранить ограниченное число значений… … Википедия
Множество (математика) — Множество один из ключевых объектов математики, в частности, теории множеств. «Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли» (Г. Кантор). Это не является в полном… … Википедия