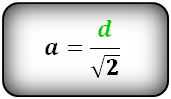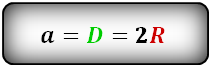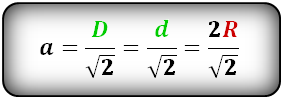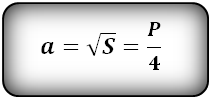Как найти сторону квадрата?
Ответ или решение 2
Нам нужно ответить на вопрос как найти сторону квадрата? Мы должны рассмотреть как минимум два возможных случая: 1) как найти сторону квадрата зная его периметр; 2) как найти сторону квадрата зная его площадь.
Отвечать на вопрос задачи будем по следующему плану
Как найти сторону квадрата зная его периметр
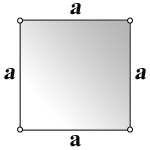
Квадратом в математике называется геометрическая фигура имеющая одинаковые углы (равные 90 градусам) и одинаковые стороны.
То есть, все стороны квадрата равны между собой.
Давайте вспомним как найти периметр квадрата.
Периметром в математике называется сумма длин всех сторон фигуры, периметр которой нужно найти.
С помощью формулы периметр квадрата можно записать так:
Если нам будет известен периметр прямоугольника, то сторону можно будет найти по формуле:
Иначе говоря, периметр нужно разделить на количество сторон (их у квадрата четыре).
Как найти сторону квадрата зная его площадь
Существует несколько формул для нахождения площади квадрата, но нам нужно вспомнить формулу площади через сторону.
Итак, зная площадь квадрата мы легко можем найти его сторону по формуле:
Иначе говоря, чтобы найти сторону квадрата нужно извлечь квадратный корень из значения площади.
У квадрата все стороны равны. Для того, чтоб найти сторону квадрата необходимо понимать, какие еще величины известны:
1) Если известна площадь квадрата, необходимо вычислить квадратный корень из площади;
2) Если известен периметр квадрата, необходимо периметр разделить на четыре.
Квадрат. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):
 |
Можно дать и другие определение квадрата.
Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).
Свойства квадрата
Изложеннные свойства изображены на рисунках ниже:
      |
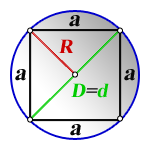
Диагональ квадрата
Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.
 |
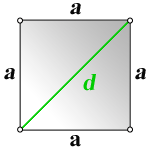
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 |
Из равенства (1) найдем d:
Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.
Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:
 |
Ответ:
Окружность, вписанная в квадрат
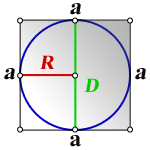
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):
 |
Формула вычисления радиуса вписанной окружности через сторону квадрата
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
 |
Ответ:
Формула вычисления сторон квадрата через радиус вписанной окружности
Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:
Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.
Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:
 |
Ответ:
Окружность, описанная около квадрата
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):
 |
Формула радиуса окружности описанной вокруг квадрата
Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.
Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:
 |
Из формулы (5) найдем R:
 |
или, умножая числитель и знаменатель на 
Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.
Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:
 |
Ответ:
Формула стороны квадрата через радиус описанной около квадрата окружности
Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.
Из формулы (1) выразим a через R:
 |
Пример 5. Радиус описанной вокруг квадрата окружности равен 
Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя 
 |
Ответ:
Периметр квадрата
Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:
где 
Пример 6. Сторона квадрата равен 
Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя 
 |
Ответ:
Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.
Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
 |
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
Так как AD и BC перпендикулярны, то
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
Эти реугольники также равнобедренные. Тогда
Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
Все формулы стороны квадрата
1. Формула стороны квадрата через диагональ
Формула стороны квадрата, ( a ):
2. Формула стороны квадрата через радиус вписанной окружности
Формула стороны квадрата, ( a ):
3. Формула стороны квадрата через радиус описанной окружности
Формула стороны квадрата, ( a ):
4. Формула стороны квадрата через площадь и периметр
Формула стороны квадрата, ( a ):
5. Формула стороны квадрата через линию выходящую из угла на середину стороны квадрата
Формула стороны квадрата, ( a ):
Квадрат. Периметр и площадь квадрата.
Рассмотрим фигуру 
Стороны AB, BC, CD, DA другое название они имеют ребра; углы A, B, C, D; второе название вершины, зеленим цветом обозначаются диагонали AD, BC. Диагонали в квадрате равны и точкой пересечения делятся пополам.
Периметр P=4•a, Площадь S=a·а
Свойства квадрата
1. Длины сторон квадрата равны.
2. Все углы квадрата прямые.
3. Противолежащие стороны квадрата параллельны друг другу AB∥CD,BC∥AD
4. Сумма всех углов квадрата равна 360 градусов ∠ABC+∠BCD+∠CDA+∠DAB=360∘
5. Величина угла между диагональю и стороной равна 45 градусов ∠BAC=∠BCA=∠CAD=∠ACD=45∘
6. Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.
7. Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника.
8. Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника.
Поделись с друзьями в социальных сетях:
Сторона квадрата
Свойства
Квадрат является правильным четырехугольников, у которого все стороны и величины всех углов равны. Это значительно упрощает вычисления, входящие в состав задачи. Диагонали, проведенные в квадрате, также равны друг другу и пересекаются под тем же углом, что и со сторонами: m(
Диагональ квадрата делит его на два конгруэнтных прямоугольных треугольника, в которых по теореме Пифагора можно вычислить сторону или диагональ квадрата. a^2+a^2=d^2 2a^2=d^2 d=√2 a
Периметр квадрата является суммой всех его сторон, а так как они одинаковы, то его можно представить в виде произведения стороны квадрата на 4. P=4a
Площадь квадрата вычисляется возведением его стороны во вторую степень. S=a^2
Радиус вписанной в квадрат окружности исходит из центра квадрата, который по совместительству является точкой пересечения диагоналей, и опускается под прямым углом на сторону. Из рисунка видно, что радиус вписанной окружности параллелен другой стороне квадрата и составляет ровно половину от ее длины. Таким образом, радиус вписанной окружности будет равен стороне квадрата, деленной на два. (рис. 69.2) r=a/2
Радиус описанной окружности исходит из центра квадрата – точки пересечения диагоналей, и опускается в угол квадрата, тем самым составляя половину диагонали квадрата. Преобразуя эту формулу для стороны получим следующее выражение. (рис. 69.3) R=d/2=(√2 a)/2=a/√2