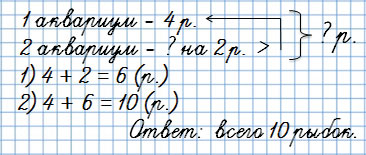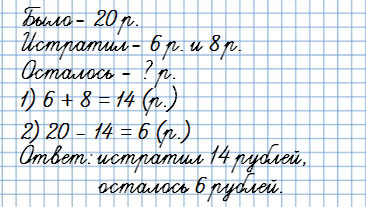Решение сложных уравнений. 3 класс.
Овладение детьми способом решения уравнений в начальной школе создает прочную основу для дальнейшего обучения алгебры, химии, физики и других предметов.
Начиная с 3-го класса, ученикам встречаются сложные уравнения, но справиться с ними очень просто.
Дети уже умеют решать простые уравнения, читай об этом здесь.
А эта статья будет посвящена решению сложных уравнений в 2-3 действия.
Очень часто родители, желая помочь, объясняют так: вот смотри, сейчас вот это число перенести в другую часть от знака равенства, надо поменять знак на противоположный: было умножение, меняем на деление; было сложение меняем на вычитание.
В начальной школе это объяснение не срабатывает, т.к. ребенок не знаком с законами алгебры.
Как сложное уравнение привести к тому, которые мы уже умеем решать, а именно к уравнению в 1 действие?
Рассмотрим уравнение в 2 действия:
х + 56 = 98 — 2 — оно достаточно легкое.
Здесь особого труда не будет в решении, потому что ребенок сразу догадается, что сначала надо 98-2.
х + 56 = 98 — 2
х + 56 = 96 – это простое уравнение. А его решаем очень быстро!
Сейчас мы рассмотрим уравнение:
Такое уравнение можно решить несколькими способами.
А когда к х + 5 – это число тоже известно.
Мы видим, что у нас получилось самое простое уравнение в 1 действие.
2 • b = 30
А чтобы найти а, нам нужно 30 : на 2.
А b не что иное, как х + 5.
х + 5 = 30 : 2
х + 5 = 15
х = 15 – 5
х = 10
Проверку делаем как обычно: переписываем первое уравнение: 2 • (10 + 5) = 30.
30 – переписываем, а левую часть считаем — будет 30.
30 = 30, значит, уравнение решили правильно.
При решении таких сложных уравнений самое главное – понять, что заменить на другое неизвестное число. Когда в уравнении всего 2 действия – это очень просто.
Наше уравнение 2 • (х + 5) = 30 читаем так: число 2 умножить на сумму х и пяти, получится 30. В данном случае – нам неизвестна сумма, чтобы ее найти, надо 30:2.
48 : (16 – а) = 4.
Если опять заменять часть уравнения другим неизвестным числом, можно запутаться. Поэтому легче использовать взаимосвязи компонентов и результата действия: число 48 разделить на разность.
Нам неизвестна разность, поэтому сначала нужно узнать чему она равна. Надо 48 : 4.
16 — а = 48 : 4
16 — а = 12 – это простое уравнение.
а = 16 — 12
а = 4
Проверка: 48 : (16 — 4) = 4
Давайте посмотрим еще одно:
Из 96 надо вычесть разность с и 16. Чтобы найти разность, надо 96-94.
Проверка: 96 — (16 — 14) = 94
А сейчас мы переходим к тем уравнениям, у которых не 2, а 3 действия. Как же нам поступать в этом случае? При решении таких сложных уравнения используем знания порядка выполнения действий в выражениях со скобками и без них.
Рассмотрим уравнение: 36 – (8 • у + 5) = 7
Прежде всего, нужно внимательно оценить левую часть уравнения: ту, которая с неизвестным числом. Вы должны четко себе представить какое вы будете делать действие первым, какое – вторым, какое – третьим: сначала делается умножение, потом сложение и последним – вычитание.
И вот то, которое вы будете делать третьим, с него и начнем, т.е. начинаем упрощать уравнение с последнего действия. Последнее действие – вычитание. С него и начнем: из числа 36 вычесть то, что в скобках и получим 7.
Значит, то что в скобках – вычитаемое, чтобы его найти, надо 36 — 7.
По правилам математики в данной записи скобки – не ставим.
8 • у + 5 = 29 – уравнение сложное. Нужно его упростить. Данное уравнение читаем так: к произведению 8 и у прибавили 5 и получилось 29. Нам неизвестно произведение, чтобы его найти, надо 29-5.
8 • у = 24 – это уравнение простое.
Итак: 7 = 7. Значит, уравнение решили правильно.
(36 + d) : 4 + 8 = 18. Определяем порядок действий: первое – сложение в скобках, второе – деление, третье сложение вне скобок. Значит, все, что до 8 – это первое слагаемое, чтобы его найти, надо 18 — 8
(36 + d) : 4 = 10 – уравнение сложное, теперь последнее действие — :, значит
36 + d = 40 – уравнение простое и его мы решаем легко!
Для удобства и быстроты решения сложных уравнений можете пользоваться данной памяткой
Дело в том, что при кажущейся сложности, если внимательно изучить все приемы, которые я вам сегодня показала, эти уравнения дети будете щелкать как семечки. Обязательно напишите в комментариях, какой способ вам более удобен.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 58
Образцы оформления задачи
В разделе «Задачи» мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
В вопросе задач такого типа всегда есть «Сколько всего?»
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
2. Задачи на нахождение остатка
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
Сколько грибов нашёл Володя?
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
4. Задачи на разностное сравнение
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
5. Задачи на нахождение неизвестного слагаемого
В условии «Было. Стало. «
В вопросе «Сколько добавили?»
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?
6. Задачи на нахождение неизвестного вычитаемого
В условии «Было. Осталось. «
В вопросе «Сколько уехало?»
«Сколько человек вышло?»
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?
7. Задачи на нахождение неизвестного уменьшаемого
В условии «Убрали. Осталось. «
В вопросе «Сколько было сначала?»
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?
Задачи в 2 и 3 действия
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
Сколько рыбок в двух аквариумах?
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?
Задачи с составлением рисунка по условию:
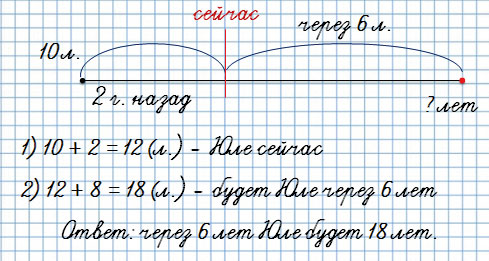
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
Поделись с друзьями в социальных сетях:
Решение простых линейных уравнений
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении: Числовой коэффициент — число, которое стоит при неизвестной переменной. Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз: Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем. Как решать простые уравненияЧтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила. 1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный. Для примера рассмотрим простейшее уравнение: x+3=5 Начнем с того, что в каждом уравнении есть левая и правая часть. Перенесем 3 из левой части в правую и меняем знак на противоположный. Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2. Решим еще один пример: 6x = 5x + 10. Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус. Приведем подобные и завершим решение. 2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок. Применим правило при решении примера: 4x=8. При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение. Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица. Разделим каждую часть на 4. Как это выглядит: Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения: Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12 Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах. Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные. Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки. Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе. Примеры линейных уравненийТеперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе! Пример 1. Как правильно решить уравнение: 6х + 1 = 19. Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1. 5х − 15 + 2 = 3х − 12 + 2х − 1 5х − 3х − 2х = −12 − 1 + 15 − 2 Ответ: х — любое число. Пример 3. Решить: 4х = 1/8. Пример 4. Решить: 4(х + 2) = 6 − 7х. Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье. Пример 5. Решить: Пример 6. Как решить линейное уравнение: х + 7 = х + 4. 5х — 15 + 2 = 3х — 2 + 2х — 1 Пример 7. Решить: 2(х + 3) = 5 − 7х. Решение задач с помощью уравнения. 3-й классКласс: 3 Презентация к урокуУрок я построила на содержании учебника математики для 3-го класса из УМК “Начальная школа ХХI века” под редакцией авторов – Виктории Наумовны Рудницкой и Татьяны Владимировны Юдачёвой. (Авторский коллектив УМК “Начальная школа ХХI века” удостоен премии Президента Российской Федерации в области образования. УМК “Начальная школа ХХI века” входит в федеральный перечень учебников, рекомендованных (допущенных) Министерством образования и науки Российской Федерации к использованию в образовательном процессе общеобразовательных учреждений.) Объяснительная часть урока не перегружена лишней информацией. Она имеет справочный характер. Ученики узнают, что многие трудные арифметические задачи можно решить с помощью составления уравнений. Сведения из истории математики, высказывание И.Ньютона (см. слайд презентации урока), приводят к возникновению проблемы: “Как перевести условие задачи с родного языка на язык алгебры?” и побуждают учащихся к поиску путей разрешения возникшего вопроса. Использование презентации к данному уроку по изучению темы: “Решение задач с помощью уравнения” помогло учащимся не только наглядно разобраться, но и научиться переводить условие задачи на язык алгебры, а также приобрести универсальные умения грамотно оформлять решение задачи уравнением. (Хотя в учебнике 3 класса и предлагается упрощённый образец оформления решения задачи уравнением, но я считаю, что рациональнее в целях преемственности и непрерывности содержания образования начинать раньше учить ребят более грамотной записи решения задач такого вида так, как этого требуют в среднем звене. Тогда у преподавателя математики не возникает проблемы переучивания, что даётся порой не всегда легко. Постепенно ученики привыкают к такому виду оформления решения задачи, и не испытывают трудности). Прослеживается система опережающего обучения Цель урока: “Провести исследование условия нескольких задач и найти новый способ решения” Ведущие задачи урока: познакомить учащихся с новым видом решения задач Время проведения урока: 2-я четверть, 3 класс. Возраст учащихся: 10 лет. Количество часов: 1 час (из четырёх). Тип урока: урок открытия новых знаний. Вид урока: урок-диалог. 1 уровень: Вова задумал число. Если к этому числу прибавить 23, то получится 52. Какое число задумал Вова? 2 уровень. У Оли было 82 рубля. Несколько рублей она заплатила за мороженое, после чего у неё осталось 63 рубля. Сколько рублей стоит мороженое? 3 уровень. В лагере 322 человека. Несколько человек ушло в поход, и в лагере осталось 275 человек. Сколько человек ушло в поход? Ход урокаI. Вводная часть. Знакомство со Смекалкиным. Слайд 2.– Ребята, к нам с вопросом обратился Смекалкин. Это внимательный и очень любознательный ученик. Сегодня на уроке он будет вам помогать обсуждать написанное в учебнике, объяснять и спрашивать. Смекалкин любит не только отвечать на ваши вопросы, но и задавать вопросы вам. А иногда и предлагать что-нибудь интересное. Хотя он иногда и попадает впросак, я всё-таки советую вам брать с него пример: не стесняться спрашивать учителя, если что-то будет непонятно. Вам желаю научиться догадываться, как Смекалкин, и проявлять инициативу. Смекалкин бы обязательно спросил: “Что такое инициатива?” Ответить можно так: инициатива – это когда ученик не только не ленится, но и не останавливается на достигнутых знаниях, всегда старается узнать как можно больше, выполнить задания как можно лучше. Инициатива в учении, да и в любом деле, – вещь важная. (Математика 5 – 6. Учебник-собеседник. Авторы: Л.Н.Шеврин, А.Г.Гейн и др. из серии “Библиотека учителя математики”, 1989 г.) II. Актуализация опорных знаний. Слайд 3.– Кто готов ответить на вопрос Смекалкина? (Мы знаем, что называется уравнением; умеем отличать уравнения от других видов выражений; умеем решать уравнения; проверять, какие числа являются корнем уравнения; определять, имеет ли данное уравнение корни) – Выбирайте себе посильное задание и, решая его, продумайте, как можно грамотно оформить ответ на заданный им вопрос. III. Проверка выполнения заданий.– Проверим, умеете ли вы рассуждать? Каждая группа доказывает правильность своего выбора и решения уравнения, нахождение корня уравнения (на экране проецируется слайд с последовательным раскрытием ответов группы)
Вывод: ваши ответы были убедительными. Вы правильно выбрали и решили именно уравнения, верно определили, какое из чисел 5, 2, 6, 3 является корнем уравнения а+ 7 = 10 и 15 – х = 9. И, конечно же, точно узнали, может ли уравнение 16 + а = 7 иметь корень. Смекалкин остался вами доволен. – А готовы ли вы пройти ещё одно испытание, которое он для вас подготовил? IV. Исследование условия нескольких задач.а) ученики записывают решение задач; б) проверка решения задач с сопроводительным объяснением. – Вызвала ли затруднение какая-нибудь задача? Каким образом вы решили 3-ю задачу? (сли покажут решение задачи так: 43 – 35 = 8 (книг), то это неплохо; тогда обратить внимание учащихся на слова в условии задач) – Есть ли разница в условии задач? Какая? (В третьей есть слово, не называющее число). – Слово несколько ключевое. Оно-то нам и будет давать сигнал к тому, как нужно действовать при решении задач такого содержания). – Смекалкин опять остался вами доволен. – А можете уже сейчас определить тему урока? ( могут и назвать, т. к. умеют пользоваться учебником: подсмотреть дома заранее; им это нравится) V. Работа с учебником.Определение темы и цели урока. – Определите тему урока. – Какие цели мы можем перед собой поставить? (ответы детей: научиться решать задачи уравнением; познакомиться с новым способом решения задач ). – Очень хорошо. Выдвинутые вами цели оказались удачными. Мы их объединим в одну и сформулируем так: Тема урока: “Решение задач с помощью уравнения” Цель: “Провести исследование условия нескольких задач и найти новый способ решения” – А чтобы каждый из Вас остался доволен результатом познания и изучения нового материала, вам нужно поставить перед собой задачи. (Дети: научиться решать задачи, составляя уравнение; научиться находить неизвестную величину.) – Задачи тоже поставлены вами нужные, но познакомившись с исторической справкой, вы поймёте, что на уроке мы будем решать задачи гораздо серьёзнее, чем вы думали. Сейчас поймёте, почему. (Задача, которую можно решить уравнением)
Если вы освоите искусство составлять уравнение по условию задачи и научитесь их безошибочно решать, то эти задачи будут вам по плечу. – Как можно перевести задачу с родного (а наш родной язык….русский) языка на язык алгебры (раздел математики). Вот как поступили наши герои Волк и Заяц. (см. стр.75, учебник математики-4 кл,. задача 1) – Вспомните, какую задачу можно решить уравнением? (Третью задачу) На полке стояло несколько книг, |
|---|