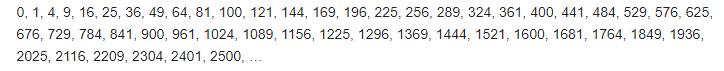Блог молодого админа
Увлекательный блог увлеченного айтишника
Как написать квадрат на клавиатуре компьютера или ноутбука?
Представим, что вы работаете с математическими примерами и появилась необходимость поставить квадрат в примере. Понятно, что слово «квадрат» будет выглядеть, мягко говоря, не к месту. Как быть? Решение есть — Windows поддерживает символ квадрата. Сейчас увидите, куда и на что необходимо нажать.
Способ первый
Используйте цифровую клавиатуру основной клавиатуры своего устройства.
Включите ее при необходимости, нажав клавишу Num Lock.
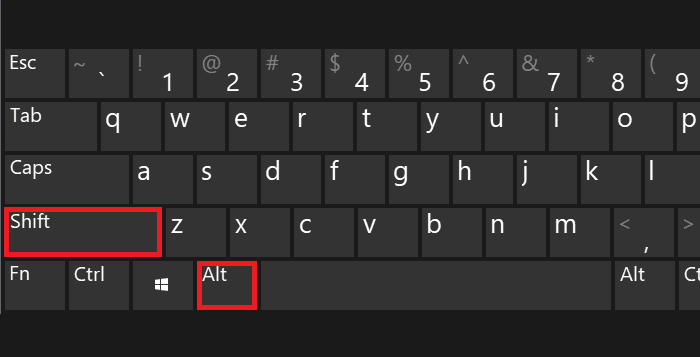
Затем зажмите Alt (левый или правый), удерживайте его и наберите на цифровой клавиатуре цифры 0178, после чего уберите палец с клавиши Alt.
Если все сделано верно, вы увидите символ квадрата сразу за нужной вам цифрой:
Если вы видите другой символ, скорее всего, дело в раскладке клавиатуры — включена русскоязычная, а нужна англоязычная. Поменяйте, нажав Shift+Ctrl:
Способ второй
Не столь удобный, но все же рабочий метод.
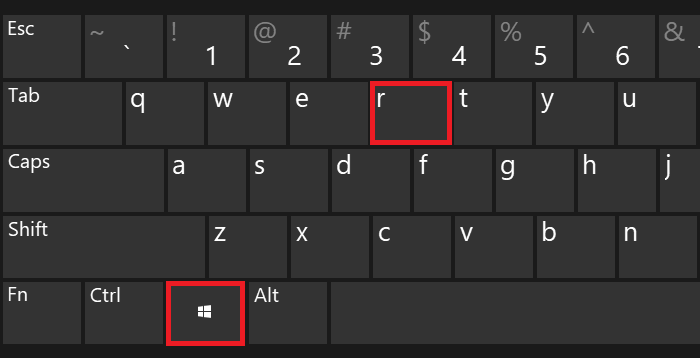
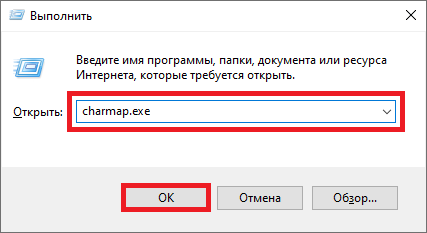
Нажмите на клавиши Win+R — чтобы вызвать окно «Выполнить».
Добавьте команду charmap.exe, нажмите ОК.
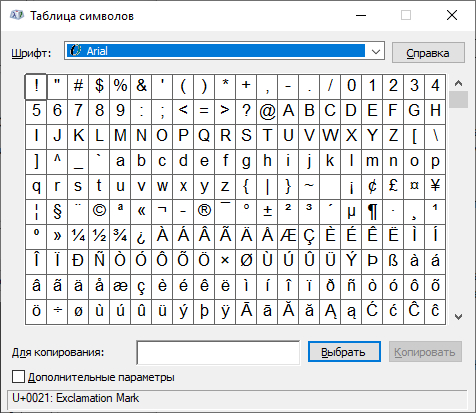
И если все было сделано верно, откроется таблица символов Windows.
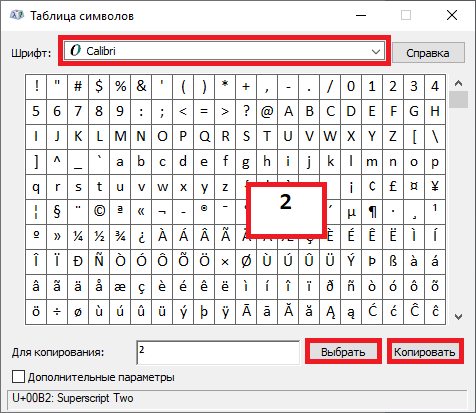
Здесь выбираете шрифт Calibri, находите знак второй степени, нажимаете на него, затем по очереди кликаете по кнопкам «Выбрать» и «Копировать».
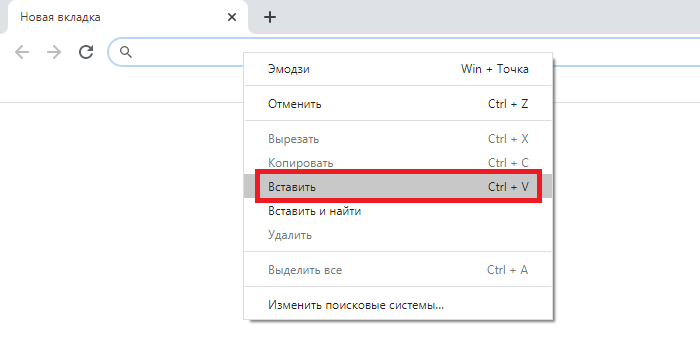
Вставляете за нужной вам цифрой.
И вот что получилось на выходе:
Согласитесь, первый способ несколько проще.
Квадратное число
Квадрат или квадратное число — целое число, которое может быть записано в виде квадрата некоторого другого целого числа (иными словами, число, квадратный корень которого целый). Геометрически такое число может быть представлено в виде площади квадрата с целочисленной стороной.
Например, 9 — это квадратное число, так как оно может быть записано в виде 3 × 3 (может быть представлено в виде квадрата 3 × 3 точки).
Содержание
Примеры
Последовательность квадратов начинается так:
0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, … (последовательность A000290 в OEIS)
| _0 | _1 | _2 | _3 | _4 | _5 | _6 | _7 | _8 | _9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0_ | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1_ | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| 2_ | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 3_ | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 4_ | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 |
| 5_ | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 6_ | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 7_ | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 8_ | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 9_ | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
Свойства
Геометрическое представление
Обобщения
Понятие квадрата обобщается на произвольные мультипликативные группы. В частности, в кольцах вычетов квадратам соответствуют квадратичные вычеты.
См. также
Примечания
Ссылки
Полезное
Смотреть что такое «Квадратное число» в других словарях:
КВАДРАТНОЕ ЧИСЛО — (от лат. quadratum. квадрат). Произведете какого нибудь числа, помноженного само на себя. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. КВАДРАТНОЕ ЧИСЛО от лат. quadratum, квадрат. Произведение какого нибудь… … Словарь иностранных слов русского языка
Центрированное квадратное число — – это центрированное полигональное число, которое представляет квадрат с точкой в центре и все остальные окружающие точки находятся на квадратных слоях. Таким образом, каждое центрированное квадратное число равно числу точек внутри данного… … Википедия
Квадратное пирамидальное число — Геометическое представление квадратного пирамидального числа: 1 + 4 + 9 + 16 = 30. В математике пирамидальное чис … Википедия
100 (число) — 100 сто 97 · 98 · 99 · 100 · 101 · 102 · 103 70 · 80 · 90 · 100 · 110 · 120 · 130 200 · 100 · 0 · 100 · 200 · 300 · 400 Факторизация: 2×2×5×5 … Википедия
200 (число) — 200 двести 197 · 198 · 199 · 200 · 201 · 202 · 203 170 · 180 · 190 · 200 · 210 · 220 · 230 100 · 0 · 100 · 200 · 300 · 400 · 500 … Википедия
Треугольное число — Треугольное число это число кружков, которые могут быть расставлены в форме равностороннего треугольника, см. рисунок. Очевидно, с чисто арифметической точки зрения, n е треугольное число это сумма n первых натуральных чисел.… … Википедия
30 (число) — 30 тридцать 27 · 28 · 29 · 30 · 31 · 32 · 33 0 · 10 · 20 · 30 · 40 · 50 · 60 Факторизация: 2×3×5 Римская запись: XXX Двоичное: 1 1110 … Википедия
Квадрат (число) — Квадрат или квадратное число целое число, которое может быть записано в виде квадрата некоторого другого целого числа (иными словами, число, квадратный корень которого целый). Геометрически такое число может быть представлено в виде площади … Википедия
10 (число) — У этого термина существуют и другие значения, см. 10 (значения). 10 десять 7 · 8 · 9 · 10 · 11 · 12 · 13 20 · 10 · 0 · 10 · 20 · 30 · 40 Факторизация: 2×5 Римская запись: X Двоичное … Википедия
Квадрат числа в математике и программировании
В этой статье мы поговорим, что такое квадрат числа, как его найти, а также каким образом производятся подобные вычисления в программировании.
Квадратом Х называют произведение 2-х множителей, каждый из которых равен Х.
Обозначение квадрата осуществляется с помощью степени, то есть Х² читается «Х в квадрате».
Если говорить еще более простым языком, то квадратом можно назвать число, которое умножено само на себя. Таким образом, мы можем написать простейшую формулу вычисления Х 2 :
Почему вообще такое выражение называют квадратом X? Дело в том, что именно данной формулой выражают площадь квадрата, сторона которого равна X, то есть геометрически это значение можно представить в виде площади квадрата, имеющего целочисленную сторону.
Вывод тут прост: для решение поставленной задачи следует требуемое значение взять в качестве множителя дважды, а потом вычислить произведение. Соответственно:
Это все элементарно и проходится в начальных классах средней школы. Решить такой пример в математике не проблема, а когда числовые значения выходят за рамки классической таблицы умножения, используют таблицу, ускоряющую расчеты.
Также описанную математическую операцию можно рассматривать в контексте частного случая возведения в степень — ведь именно этим, по сути, она и является — возведением в степень 2.
Интерес представляет и числовая последовательность для квадратов целых чисел, являющихся неотрицательными (речь идет о последовательности A000290 в OEIS):
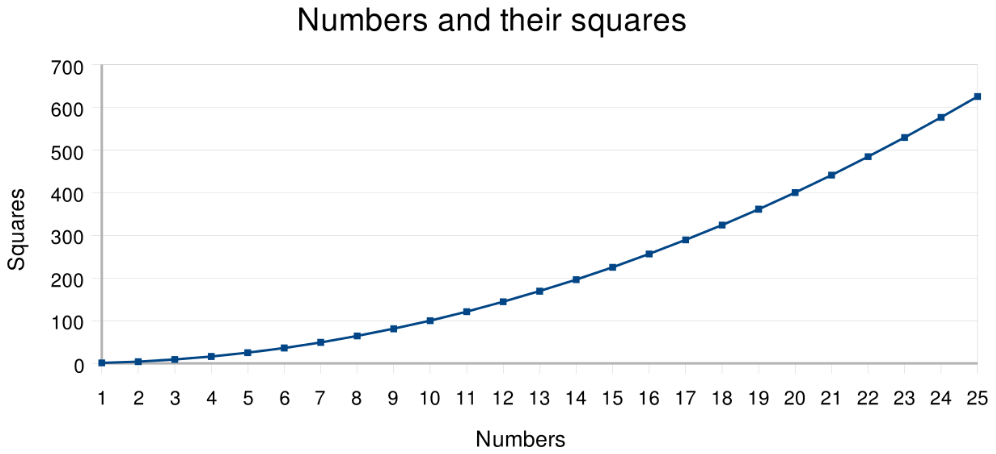
Нельзя не сказать и про график y=x², где представлены целые значения x на отрезке 1-25.
Квадратные числа
Если же говорить о натуральных числах из последовательности, упомянутой выше, в историческом контексте, то их всегда называли «квадратными». Квадратное числовое значение также называют полным либо точным квадратом, то есть целым значением, квадратный корень из которого можно извлечь нацело. К примеру, найти корень из 9 несложно (√9 = 3, т. к. 3 ⋅ 3 = 9). Не составляет проблем и вычислить корень из ста: (√100 = 10, ведь десять на десять равно сто).
А что в программировании?
Теперь давайте посмотрим, как все это работает в программировании. Для примера возьмем такой язык программирования, как Java (кстати, статья о том, как выполнять возведение в степень в Java, уже была).
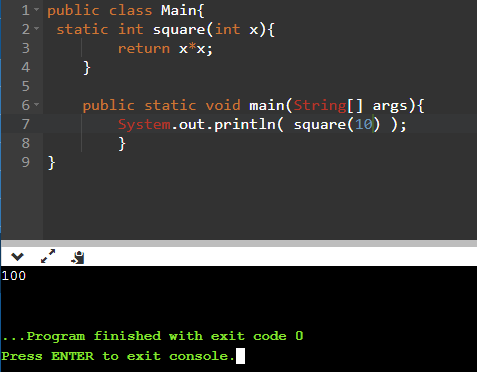
Напишем простой метод по возведению любых числовых значений в квадрат:
static int square(int x)<
public static void main(String[] args)<
Вы можете воспользоваться любым онлайн-компилятором для проверки этого кода. Также никто не мешает вписать любое число вместо десяти.
Теперь воспользуемся простейшей программой для того, чтобы найти квадратный корень из 100:
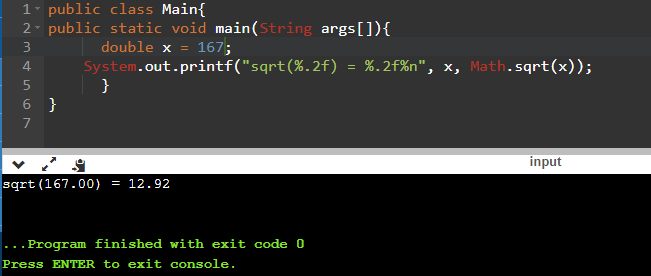
public static void main(String args[])<
System.out.printf(«sqrt(%.2f) = %.2f%n», x, Math.sqrt(x));
Программа позволяет извлекать корень и из неквадратных значений. Ниже мы находим корень из 167:
Да, в современную эпоху калькуляторов мало кто считает в уме. Вдобавок ко всему, сегодня даже не надо покупать настоящий калькулятор, так как калькулятор есть в любом мобильном телефоне, не говоря уже об онлайн-калькуляторах, коих существует огромное количество. Однако это не значит, что можно забыть азы алгебры. Не зря же великий русский ученый Михаил Ломоносов когда-то сказал:
Компьютерная грамотность с Надеждой
Заполняем пробелы — расширяем горизонты!
Как написать степень на клавиатуре в Word или Блокноте
Числа бывают не только простые. Порой числа возводят в степень: в квадрат (во вторую степень), в куб (в третью), и вообще в любую другую степень. Как это записать на бумаге – понятно. Ставишь возле числа сверху еще одно дополнительное число «2», либо «3» или любое другое – вот вам и степень числа.
А вот как написать степень на клавиатуре в Блокноте или в Word? Ведь на клавиатуре нет маленьких чисел для обозначения степеней.
Два кода, чтобы написать степень в квадрате и в кубе
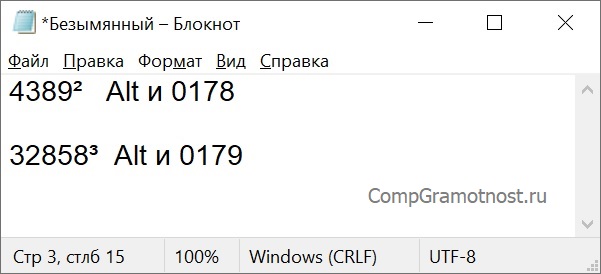
Рис. 1. Вторая и третья степень появились в Блокноте с помощью комбинаций клавиш.
Проблема в том, что клавиатура не оснащена такой клавишей, которая позволила бы вот так просто поставить степень. Но для этого существуют специальные комбинации клавиш:
«Alt+0178» – с ее помощью можно написать вторую степень (²);
«Alt+0179» – используя эту комбинацию, можно написать третью степень (³).
Однако не все так просто, есть нюансы.
Как написать степень на клавиатуре с помощью кодов
1) Перед тем как воспользоваться вышеперечисленными комбинациями, следует убедиться, что выставлен английский язык.
2) Затем нужно активировать цифровую панель путем нажатия на «Num Lock». Такую панель называют еще малой цифровой клавиатурой.
На полноразмерной клавиатуре из 104 клавиш малая клавиатура находится справа на отдельной панели. Там достаточно один раз нажать на клавишу «Num Lock».
На ноутбуке в силу его компактных размеров малая цифровая клавиатура находится обычно на основной клавиатуре. Чтобы ее активировать, чаще всего надо, удерживая вспомогательную клавишу «Fn», нажать на «Num Lock».
3) Поставить курсор в то место текста, куда требуется вставить степень.
4) Удерживая клавишу «Alt», поочередно набрать цифры на малой клавиатуре, например, 0, 1, 7, 8. Отпустив «Alt», на экране сразу увидим степень 2 («в квадрате»).
Также удерживая «Alt», можно последовательно нажать на малой цифровой клавиатуре цифры 0, 1, 7, 9. Отпустив «Alt», получим 3 степень («в кубе»).
Частая ошибка при вводе степени числа. Зажав «Alt», можно по идее набирать цифры 0, 1, 7, 8 или 0, 1, 7, 9 с помощью тех цифровых клавиш, что находятся на основной клавиатуре в ее верхнем ряду. Но степень 2 или 3 в результате комбинации таких клавиш, увы, НЕ появится. Необходимо код 0178 набирать только с помощью клавиш малой цифровой клавиатуры. Хотя, казалось бы, чем могут отличаться цифры на обычной клавиатуре и на малой цифровой клавиатуре? Тем не менее – они отличаются, и еще как.
5) Затем можно выключить цифровую панель, нажав на «Num Lock». На ноутбуке, как правило, надо зажать «Fn», потом нажать «Num Lock» и панель будет выключена.
Этот способ для ввода степени числа работает в большинстве стандартных текстовых редакторах, например, в Word и в Блокноте.
«Надстрочный знак» в Word, чтобы напечатать любую степень числа
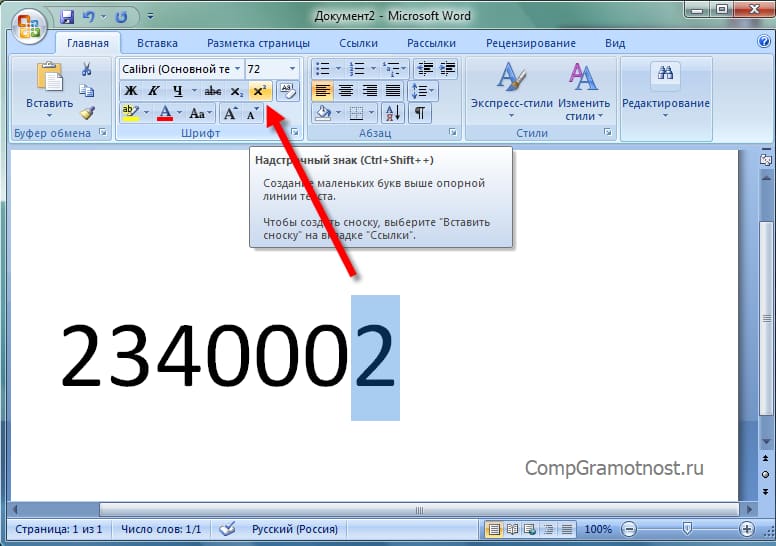
В Word есть встроенная кнопка, при помощи которой можно написать степень числа на клавиатуре. Она называется «Надстрочный знак» («X²») и располагается во вкладке «Главная».
Рис. 2 (Клик для увеличения). «Надстрочный знак» («X²») во вкладке «Главная» позволяет написать степень числа.
Кроме цифр, можно также превращать в степень и буквы. Так можно сделать текст маленького размера и поместить его наверху строки текста.
Такое выделение текста, возможно, кому-то понадобится в разных ситуациях. Так что кнопка Ворда для написания степени числа является универсальной. Она превращает в «степень» любую последовательность символов.
Пункт «Надстрочный» превращает любой символ в степень
Этот вариант работает во всех версиях Word, в том числе в устаревших.
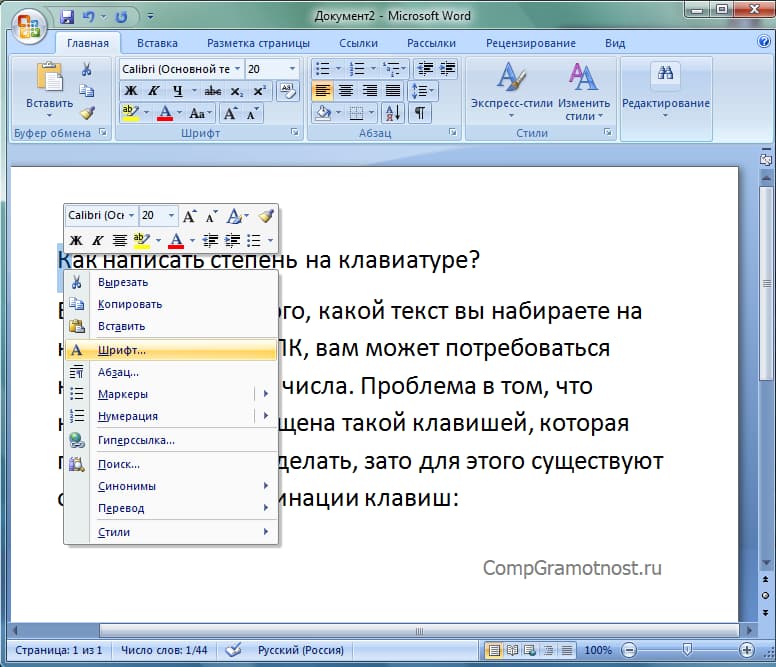
Рис. 3. Выделен символ «К». Клик по нему с помощью правой кнопки мыши открывает меню с опцией «Шрифт».
Процесс написания степени числа осуществляется следующим образом:
1) Необходимо выделить число или букву, которому требуется придать вид степени.
2) Затем кликнуть по выделенному числу ПКМ (правой кнопкой мыши).
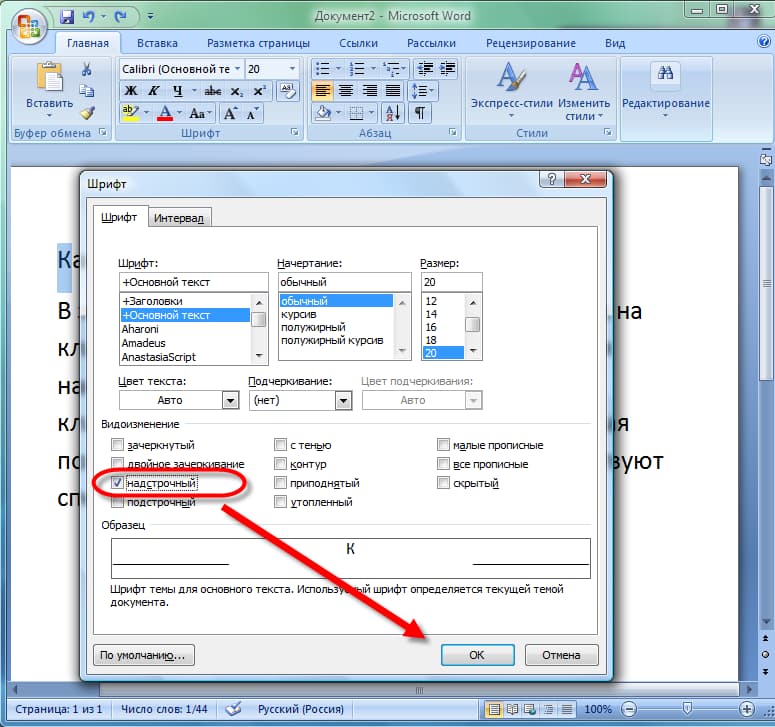
3) Далее следует перейти в «Шрифт» и отметить пункт «Надстрочный».
4) Нажать «OK», чтобы подтвердить действия.
Рис. 4 (Кликните для увеличения). Меню «Шрифт» с опцией «надстрочный».
После выполнения этих несложных действий выделенная цифра или буква примет вид степени числа. Выделять также можно не только отдельную букву или символ, но и любую длинную последовательность символов. Тогда вся выделенная последовательность приобретет вид «надстрочный».
Таблица символов для ввода степени
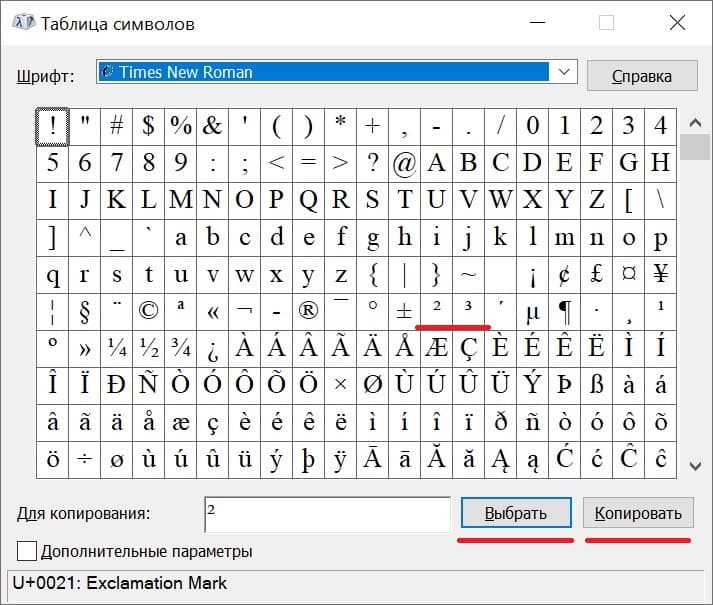
Рис. 5. Таблица символов. Выделены степени 2 и 3.
В операционной системе Windows есть Таблица символов. Она позволяет найти и вставить в свой текст какой-либо символ, которого нет на клавиатуре.
1) В строке поиска набираем: таблица символов. Будет найдена таблица, надо ее открыть.
2) Открываем шрифт «Times New Roman» (рис. 5), либо «Arial» или по своему выбору. В указанных шрифтах есть 2 и 3 степень. Кликаем по ней и нажимаем кнопку «Выбрать». Степень появится в поле «Для копирования».
3) Далее жмем кнопку «Копировать». Таким образом, выбранная степень будет скопирована в буфер обмена, то есть в оперативную память компьютера.
4) Ставим курсор в то место, где требуется вставить степень. Нажимаем на кнопку «Вставить», которая находится в Ворде в левом верхнем углу.
Демонстрация степени числа или написание надстрочных символов позволяет украшать текст, делать его более привычным и понятным для восприятия.
Нашли ошибку? Выделите фрагмент текста и нажмите Ctrl+Enter.
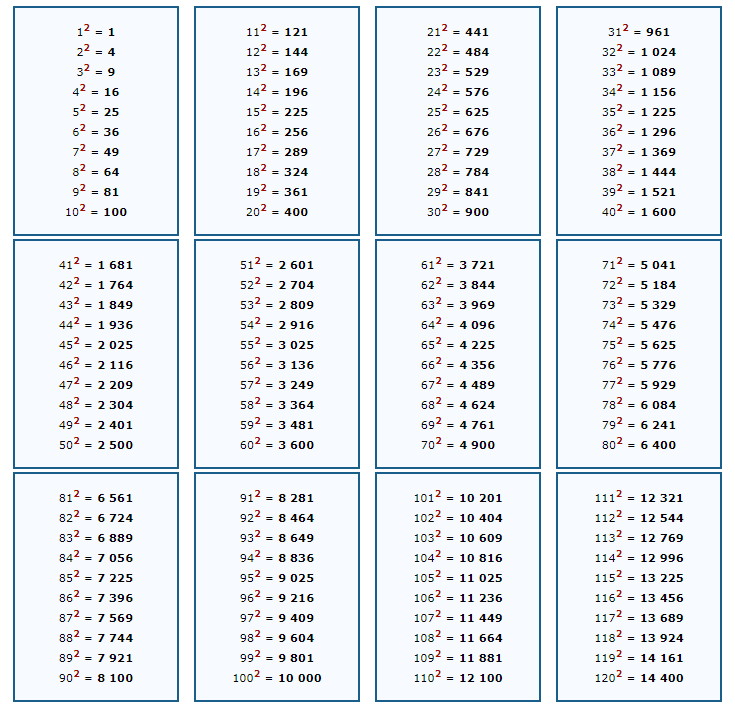
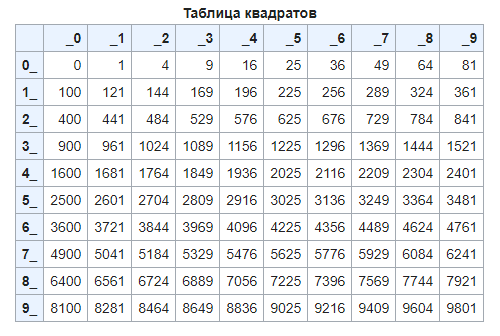
Таблица квадратов
Таблица квадратов или таблица возведения чисел во вторую степень. Интерактивная таблица квадратов и изображения таблицы в высоком качестве.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
Таблица квадратов
Теория
Квадрат числа – это результат умножения числа само на себя. Операция вычисления квадрата числа – это частный случай возведения числа в степень, в данном случае во вторую:
Данное выражение читается: «возвести в квадрат число 6» или «6 в квадрате».