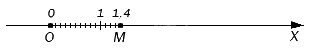Дробные числа
Типографика. Числа и знаки. Количественные числительные.
Форма набора простых дробей
Простые дроби принято набирать цифрами на верхнюю и нижнюю линии шрифта: 3/4. Но для набора именно таким образом наборщик должен получить письменное указание. Поэтому в оригинале простые дроби, написанные в одну линию через косую черту, следует пометить верхней или нижней дугой, повторить ее на боковом поле и рядом написать в кружке: дробь. Напр.:
В выборах приняла участие всего

Простую дробь набирают без отбивки от целого числа. Напр.: 51/2.
Форма набора десятичных дробей
Дробная часть десятичных дробей, как и целые числа, делится пробелами на группы по 3 знака в каждой, но в обратном направлении по сравнению с целыми числами, т. е. слева направо. Напр.:
25,128 137; 20 158,675 8
Падеж существительных при дробных числах
Дробное число управляет существительным при нем, и поэтому последнее ставят в род. падеже ед. ч. Напр.: 1/3 метра; 0,75 литра; 0,5 тысячи; 105/6 миллиона.
Употребление слов «часть», «доля» при дробных числах
Как правило, следует считать словесным излишеством употребление слов часть, доля после простых дробных чисел. Напр.:
Поиск ответа
| Вопрос № 307952 |
Здравствуйте. Задаю свой вопрос во второй раз и все же надеюсь, что вы мне ответите. Возможно ли сокращение слов » десятич ный» и «шестнадцатеричный» таким образом: 10-тичный, 16-теричный? И если нет, то возможно ли в принципе написание этих слов в буквенно-цифровой форме? Я знаю об общем правиле сокращения слов, включающих в себя числа, типа 150-летие или 20-тонный. Однако конкретно таких слов в буквенно-цифровом виде я не видела и очень сильно сомневаюсь, что их можно писать подобным образом. Автор текста настаивает на сокращении.
Ответ справочной службы русского языка
Такие сокращения не являются общепринятыми, они будут непонятны читателю. Наша рекомендация — не сокращать.
Добрый день! Подскажите, пожалуйста, как правильно написать словами «74-километровый»: семи десятич етырехкилометровый или семидесяти четырехкилометровый?
Ответ справочной службы русского языка
Правильно: семи десятич етырехкилометровый.
Ответ справочной службы русского языка
В сочетании с дробным числительным существительное ставится в форме единственного числа родительного падежа.
Здравствуйте! Подскажите, каким правилом руководствоваться, когда формируются фразы «в N раз(а)», где N – число с десятич ными долями. Например: в 1,5 разА, в 2,7 раз(А?) и т.п.
Ответ справочной службы русского языка
При дробных числах существительные ставятся в форме единственного числа родительного падежа: в 1,5 раза, в 2,7 раза.
Добрый день, уважаемые эксперты. Я патрулирующий русской Википедии. В своей работе нередко сталкиваюсь с числительными, а именно с денежными наименованиями. Постоянно возникают трудности с десятич ными дробями. Не знаю как склонять существительные рядом с ними. Например, 2,89 миллиардА или миллиардОВ доллара(-ов). Обычно проверяю себя, проговаривая дробное число: «Две целых восемьдесят девять сотЫХ миллиардОВ долларОВ», но не знаю, правильно ли это. Можете, пожалуйста, объяснить и просклонять данное число и, например одна целая тридцать одна сотая. Благодарю.
Ответ справочной службы русского языка
Правило простое: при дробных числительных существительное употребляется в форме единственного числа родительного падежа: 4,3 рубля, 67,84 километра, 2,89 миллиарда. Слово доллар уже не зависит напрямую от числительного, поэтому ставится во множественном числе: 2,89 миллиарда (чего?) долларов.
Поэтому верно: Две целых восемьдесят девять сотых миллиарда долларов; одна целая тридцать одна сотая миллиарда долларов.
Доброго времени суток! Возникла трудность со склонением десятич ных дробей, и ответ найти самостоятельно не получилось. Ниже представлен пример предложения. Прошу помочь разобраться с этим. Если масса половины кубического дециметра вещества равна нулю целым сорока пяти сотым килограмма, то масса одного кубического дециметра вещества равна нулю целых девять десятых килограмма. (Написано по-разному для наглядности вариантов). Спасибо за помощь!
Ответ справочной службы русского языка
Склоняются все части числительного. Верно: Если масса половины кубического дециметра вещества равна нулю целым сорока пяти сотым килограмма, то масса одного кубического дециметра вещества равна нулю целым девяти десятым килограмма.
Обратите внимание, что слова ноль целых обычно опускаются.
Ответ справочной службы русского языка
Союз не нужен: десять целых пять десятых.
Ответ справочной службы русского языка
В русском языке в дробных числах ставится запятая, а не точка. Например: 6,87.
Уважаемые специалисты! Я уже задавала Вам похожий вопрос и получила на него ответ, за что Вам очень благодарна. Большое спасибо! Позвольте, пожалуйста, вопрос ради уточнения. Дело в том, что я не могу найти похожий вопрос среди других вопросов на Вашей сайте. После десятич ных дробей имя существительное всегда стоит в родительном падеже единственном числе. Например, три целых две десятых яблока или семь целых четыре десятых окна. Верно? А вот например, три целых две десятых тысячи автомобилей или семь целых четыре десятых миллиона дорог. Второе имя существительное «автомобилей» и «дорог» всегда стоит в родительном падеже множественном числе? Правило о том, что один автомобиль; два, три, четыре автомобиля; пять, шесть и т. д. автомобилей сюда не подходит? Очень прошу ответить на мой вопрос! Пожалуйста! Заранее благодарю Вас.
Ответ справочной службы русского языка
Правильно, например: три яблока, три целых две десятых яблока, три целых две десятых тысячи яблок; пять яблок, пять целых семь десятых яблока, пять целых семь десятых миллиона яблок.
Объясните, пожалуйста. Мой вопрос касается имён существительных, которые употребляются после десятич ный дробей. Как будет правильно? Семь целых шесть десятых ЯБЛОКА или ЯБЛОК? Восемь целых пять десятых ТЫСЯЧИ или ТЫСЯЧ? Восемь целых пять десятых ТЫСЯЧИ или ТЫСЯЧ автомобилей? Заранее благодарю за ответ!
Ответ справочной службы русского языка
Существительным управляет дробная часть: семь целых шесть десятых яблока, восемь целых пять десятых тысячи автомобилей.
Меня интересуют окончания слов после десятич ных дробей: 422,8 квадратн(ых, ого) метр(ов, а). Ответ нужен срочно.
Ответ справочной службы русского языка
Существительным управляет дробная часть: 422,8 квадратного метра (восемь десятых чего? квадратного метра).
Скажите пожалуйста, какой вариант правильнее использовать с десятич ными дробями: миллиардА или миллиардОВ (миллионА или миллионОВ). Напр. 3,5 миллиарда/миллиардов, 8,2 миллиарда/миллиардов, 21,7 миллиона/миллионов. Зависит ли правильная форма от конкретной цифры? Если да, подскажите пожалуйста общее правило. Спасибо!
Ответ справочной службы русского языка
Существительным управляет дробная часть, поэтому нужен родительный падеж единственного числа: 3,5 миллиарда, 8,2 миллиарда, 21,7 миллиона (пять десятых миллиарда, две десятых миллиарда, семь десятых миллиона).
Здравствуйте. Существует ли какое-то правило по поводу произношения (выбора) «года» или «лет» в десятич ных дробях? Например, «Средний возраст составляет 30.4 года» и
«Повысился до 30.4 лет». Спасибо.
P.S. В корректности примеров не уверен.
Ответ справочной службы русского языка
Если в словосочетании существительное зависит от дробного числительного, то существительное ставится в форме родительного падежа единственного числа: 30,4 года; до 30,4 года.
Ответ справочной службы русского языка
Не следует использовать один и тот же знак как знак перечисления и как знак-разделитель между целой и дробной частью числа. Постановка точки с запятой оправданна.
Подскажите, пожалуйста, как написать «84-пушечный корабль» прописью.
С уважением, Мария
Ответ справочной службы русского языка
Десятичные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Десятичные дроби: определения, запись, примеры, действия с десятичными дробями
Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.
Что такое десятичная запись дробных чисел
Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.
Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.
Определение десятичных дробей
Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:
Десятичные дроби представляют собой дробные числа в десятичной записи.
О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.
Как правильно читать десятичные дроби
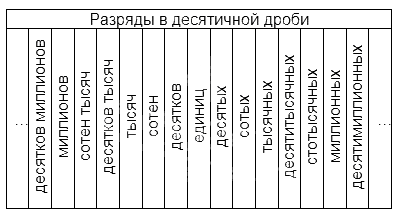
Что такое разряды в десятичных дробях
Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:
Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.
Что такое конечные десятичные дроби
Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:
Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.
Основные виды бесконечных десятичных дробей: периодические и непериодические дроби
Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.
Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.
В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.
Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.
Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.
Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.
Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.
К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.
Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.
Основные действия с десятичными дробями
С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.
Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.
Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.
Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.
Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.
Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.
Положение десятичных дробей на оси координат
Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.
Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.
Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.
Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.
Понятие десятичной дроби
В данной публикации мы рассмотрим, что из себя представляет десятичная дробь, как она пишется и читается, какой обыкновенной дроби соответствует и в чем заключается ее основное свойство. К теоретическому материалу прилагаются примеры для лучшего понимания.
Определение десятичной дроби
Десятичная дробь – это особый вид записи обыкновенной дроби, знаменатель которой равен 10, 100, 1000, 10000 и т.д.
Такие дроби вместо привычного варианта написания ( с числителем, знаменателем и черточкой-разделителем), принято записывать так: 0,3 ; 2,6 ; 5,62 ; 7,238 и т.д.
Десятичные дроби бывают двух типов:
Запись десятичной дроби
Десятичная дробь состоит из целой и дробной частей, между которыми находится десятичный разделитель – в виде запятой или точки.
Соответствие десятичной дроби обыкновенной:
Примеры:
, т.к. после запятой одна цифра.
, т.к. после запятой одна цифра.
, т.к. после запятой две цифры.
, т.к. после запятой три цифры.
Примечание: Если в десятичной дроби сразу после запятой идут нули и затем только цифры, то в виде обыкновенной дроби это выглядит так: числитель – только цифры без нулей, знаменатель – единица и количество нулей, соответствующее количеству цифр после запятой.
Например:
Чтение десятичной дроби
Читается десятичная дробь следующим образом: сначала произносится целая часть с добавление слова “целых”, затем дробная – с указанием разряда, который зависит от количества цифр после запятой:
Например:
Основное свойство десятичной дроби
Величина десятичной дроби не изменится, если справа к ней добавить любое количество нулей. Т.е. если такие нули встречаются, их можно просто отбросить (только те нули, которые расположены справа от цифр в дробной части).
Например:
Теперь вы знаете какие однокоренные слова подходят к слову Как правильно прописью написать десятичную дробь, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову "Как правильно прописью написать десятичную дробь", предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором.