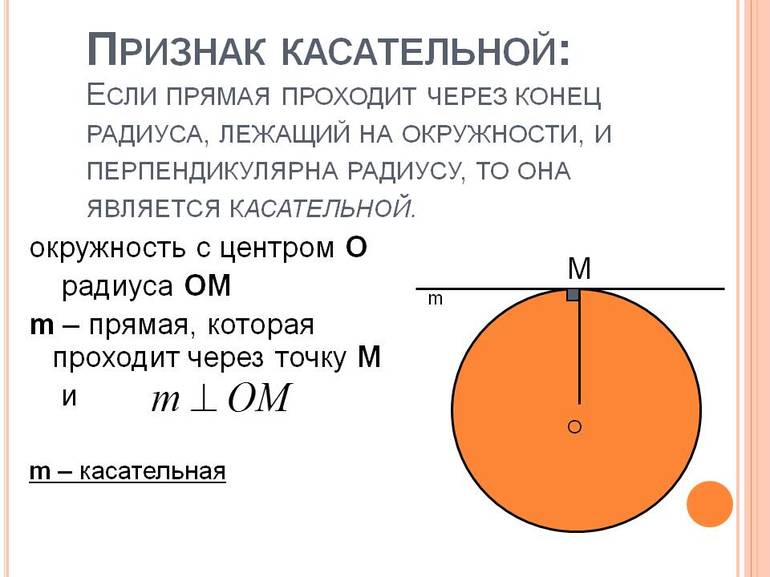
Касательная (геометрия)
Было бы неправильно, как это иногда делается, определить касательную как прямую, которая «касается кривой, но не пересекает ее», поскольку
Аналогом понятия касательной к поверхностям является понятие касательной плоскости. Его можно определить, рассматривая набор кривых, нарисованных на поверхности и проходящих через заданную точку, и рассматривая набор полученных касательных. Затем мы можем обобщить на объекты размерности больше 2.
Резюме
Геометрическое определение касательной
Касательная к кривой C в точке A абсциссы a является предельным положением, если оно существует, секущей линии (AB), когда точка B кривой стремится к точке A.
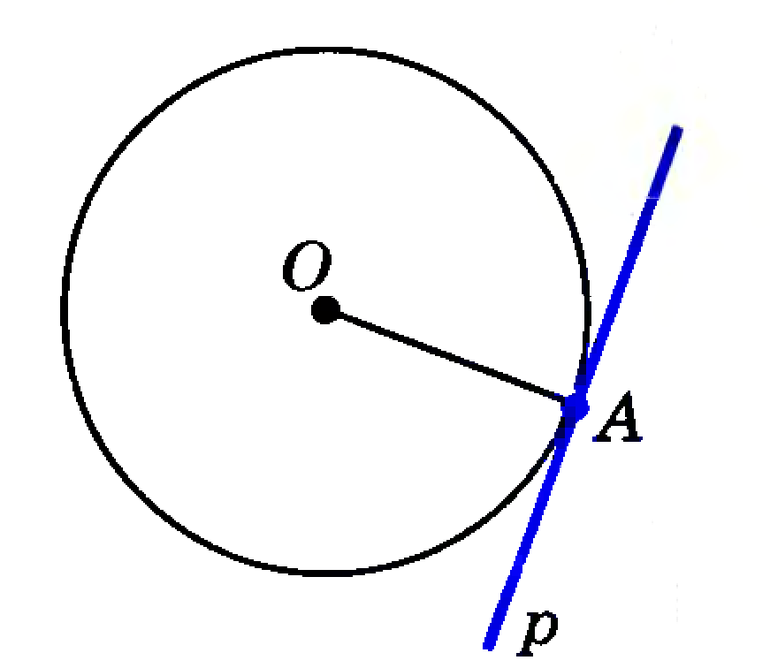
Пример: касательная к окружности
Угол между двумя кривыми
Рассмотрим две кривые C и C ‘, проходящие через одну и ту же точку M; предполагается, что в этой точке у них обоих есть касательные.
Расчет касательной
Касательная к числовому функциональному графу
По касательной к параметрической дуге
Связь с дифференциальным исчислением
Если f допускает последовательность нулевых производных по a, то первая ненулевая производная, идущая к порядку p
тогда идет касательная, направленная по первой ненулевой производной. В такой точке мы говорим, что существует контакт порядка p между кривой и ее касательной (в то время как в регулярной точке контакт имеет только порядок 1).
Половина касательных
Мы говорим, что имеется полукасательная вправо, когда существует следующий предел
Мы говорим, что есть полукасательная слева, когда существует следующий предел (обратите внимание на порядок)
Если есть полукасательные, мы используем следующий словарь:
График функции абсолютного значения дает пример угловой точки
В случае дельтовидной мышцы мы видим три бугорка.
Кривая в полярных координатах
Касательная для неявной кривой
Рассмотрим кривую декартовой уравнения Р (х, у) = C в евклидовой плоскости, для функции F из класса на открытой одной плоскости. ПРОТИВ 1 <\ Displaystyle <\ mathcal
Положение относительно касательной
Выпуклость
График дифференцируемой числовой функции выпуклый тогда и только тогда, когда кривая всегда находится выше своих касательных. Она вогнута тогда и только тогда, когда кривая находится ниже своих касательных.
В тех случаях, которые встречаются на практике, кривая попеременно вогнута или выпукла на различных интервалах, разделенных точками перегиба (для которых касательная пересекает кривую).
Использование дифференциального исчисления для замечательных точек
В этом кадре дуга принимает вид ( X ( t ), Y ( t )). Затем мы выполняем ограниченное разложение функций X и Y :
Распространение на поверхности и за их пределы
Касательная в художественном рисовании
В рисовании и анимации художники стараются избегать касания двух кривых. Действительно, касание рискует нарушить эффект перспективы, поскольку мы не знаем, какая поверхность находится перед другой, с одной стороны; и, с другой стороны, прямые линии, касательные к двум кривым, образуют крест, который притягивает взгляд и не позволяет ему перемещаться по рисунку.
Общие сведения
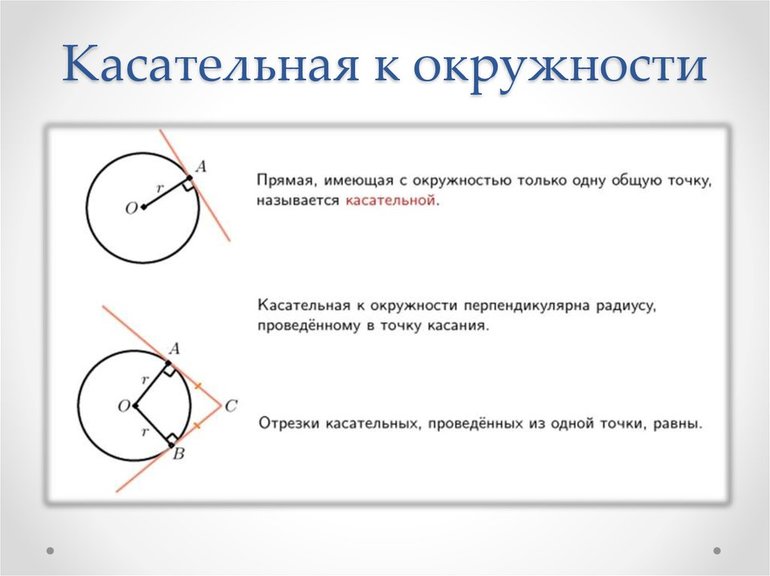
Важно знать терминологию, соотношения и теоремы для решения задач этого класса. Касательной к окружности называется прямая, которая имеет с ней только одну точку соприкосновения. Прямая — это линия, не имеющая границ, т. е. она ничем не ограничена. Окружностью называется геометрическое место точек, удаленных от центра на одинаковые расстояния.
Следует отметить, что касательные бывают внешними и внутренними. Внешней называет прямая линия, проходящая с внешней стороны окружности. Внутренние касательные пересекают отрезок, который соединяет центры двух окружностей. Последний тип прямых не существует, когда два круга пересекаются. Касательные нужно уметь правильно строить, поскольку от этого зависит правильность решения задачи.
Построение касательных
Для построения касательной к окружности следует на последней отметить произвольную точку. Затем необходимо через нее провести прямую. Нужно отметить, что у круга может быть несколько таких прямых. Когда даны две окружности, тогда можно проводить не только внешние, но и внутренние. Существует определенный алгоритм, по которому можно построить первый тип:
Существует более простая модель построения таких прямых. Для этого следует начертить один круг, а затем отметить две произвольные точки на его противоположных сторонах. Далее начертить II круг, превышающий I по радиусу. Отметить на нем точки, воспользовавшись подобием, т. е. они должны быть в тех же местах, что и на I. Затем провести прямые, которые должны соприкасаться с I и II кругами только в одной точке.
Для построения внутренних касательных существует определенная методика. В интернете можно найти много информации. В одних источниках алгоритм построения является сложным, а в других — простым. Однако есть один метод, позволяющий осуществить данную операцию. Специалисты описали его на «понятном» языке для новичков. Суть методики заключается в следующем:
Далее нужно рассмотреть некоторые свойства, на основании которых можно решать задачи и доказывать геометрические тождества.
Основные свойства
Свойства — утверждения, полученные в результате доказательства теорем о касательной к окружности. Первые нет необходимости доказывать, поскольку об этом уже позаботились математики. Они выделяют всего 4 свойства касательных к окружности:
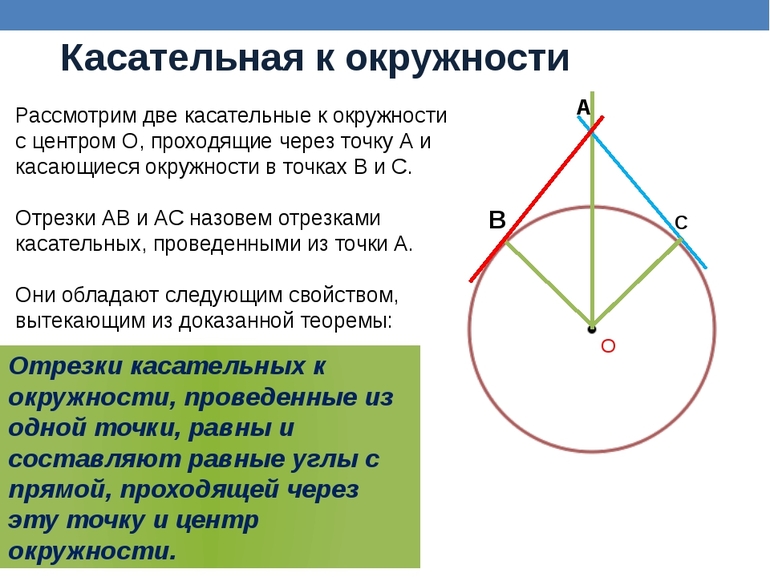
Для рассмотрения I свойства необходимо начертить окружность с центром О1. Затем нужно отметить точку М вне окружности. Из М провести одну прямую, которая соприкасается с кругом в точке А. Такую же операцию следует проделать и для другой касательной. Точку соприкосновения назвать В. Отрезки АМ и ВМ равны между собой.
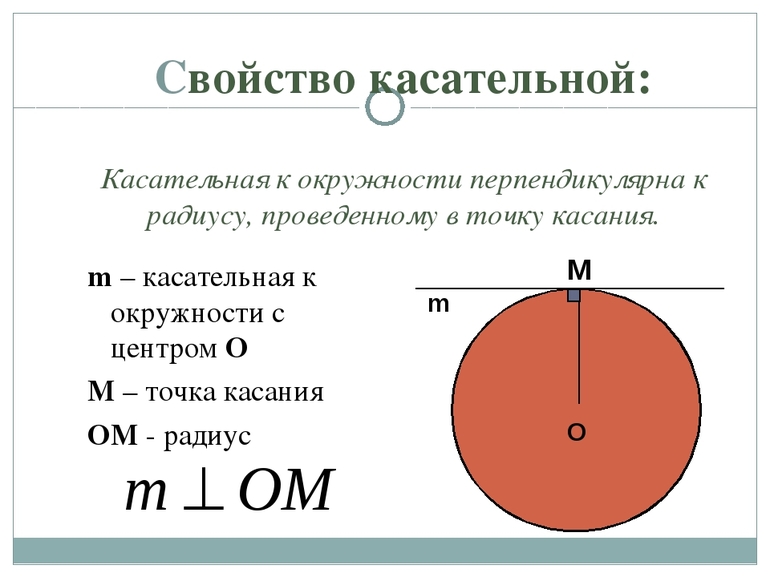
Если провести радиусы к точкам А и В, то можно сделать вывод, что углы являются прямыми. Чтобы понять третье свойство, необходимо начертить окружность и отметить некоторую точку М за ее пределами. После этого следует из искомой точки провести секущую и касательную. Первой называется прямая, проходящая через окружность и пересекающая ее в двух точках. Для касательной точку соприкосновения необходимо обозначить А. Тогда секущая пересекает круг в точках В (ближняя) и С (дальняя). В результате этого получается такое соотношение: АМ 2 = АВ * МС.
Когда для произвольной окружности существуют касательная и секущая, тогда между ними образуется некоторый угол.
Хорда, полученная в результате прохождения через окружность, образует также угол. Он опирается на искомую хорду и является вписанным. Следовательно, по свойству градусные меры углов равны между собой. Далее нужно разобрать частные случаи, на основании которых можно сделать вывод о количестве касательных.
Когда окружность вписана в ромб, тогда их точки касания нужно рассматривать по первому свойству. Радиус окружности можно найти по следующим формулам:
Следует отметить, что у ромба две диагонали. Они различаются по размеру. Одна из них больше другой (d1 > d2).
Частные случаи
В некоторых задачах нужно определить количество касательных у двух окружностей. Можно выполнить ряд сложных и трудоемких доказательств. В результате этого будет потрачено много времени, а можно воспользоваться уже готовыми дополнительными свойствами:
Когда заданы окружности, радиус одной из которых равен 0, тогда «нулевой» круг эквивалентен двойной точке. Прямая является двойной и проходит через эту точку. В этом случае математики определяют всего две внешних. Если r1 = r2 = 0, то всего 4 внешних общих касательных. Далее для решения задач нужно разобрать доказательства некоторых свойств.
Доказательства утверждений
Очень важно знать доказательства некоторых свойств и теорем, поскольку одним из типов задач считаются упражнения повышенной сложности, требующие логических расчетов в общем виде. Например, нужно доказать, что касательная образует с радиусом, проведенным к точке касания, прямой угол. Существует тип доказательства от противного.
Следует отметить, что уравнение окружности с радиусом, равным единице, описывается функцией x 2 + y 2 = 1. Эта запись применяется для решения задач в общем виде. Прямая — функция, описанная прямой пропорциональностью у = кх + b. Чтобы связать окружность и касательные, нужно составить систему уравнений. Этот математический ход объясняется тем, что у функций должны быть общие решения (точка на окружности). После решения можно выполнить проверочные вычисления, подставив корни в систему.
Таким образом, для решения задач об окружности и касательной следует знать общие понятия, а также основные свойства и теоремы.
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.
Получаем формулу для нахождения секущей вида:
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.
Решение
Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3
Отсюда следует, что α x = a r c t g 3 3 = π 6
Ответ: уравнение касательной приобретает вид
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
Для наглядности изобразим графически.
Решение
Необходимо продифференцировать функцию. Имеем, что
Вычисляем соответствующие значения функции
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
Другое уравнение имеет два действительных корня, тогда
Перейдем к нахождению значений функции. Получаем, что
Возможно существование бесконечного количества касательных для заданных функций.
Решение
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у :
Ответ: необходимы уравнения запишутся как
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Данное равенство может быть записано как объединение двух функций:
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Касательная к эллипсу
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
Решение
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид
Графически касательные обозначаются так:
Касательная к гиперболе
Гипербола может быть представлена в виде двух объединенных функций вида
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
Ответ: уравнение касательной можно представить как
Наглядно изображается так:
Касательная к параболе
Графически изобразим как:
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.
Отсюда определим значение х для точек касания.
Первая функция запишется как
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.
Вторая функция запишется как
Ответ: уравнение касательной принимает вид
Касательная к окружности
Касательная к окружности, секущая и хорда — в чем разница
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.