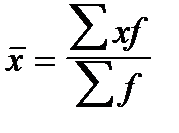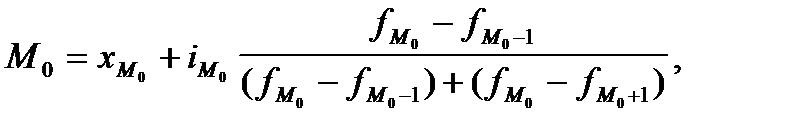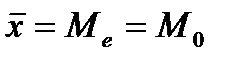Графическое изображение вариационного ряда
Графическое изображение вариационных рядов облегчает их анализ и позволяет судить о форме распределения. Для графического изображения вариационного ряда в статистике строят гистограмму, полигон и кумуляту распределения.
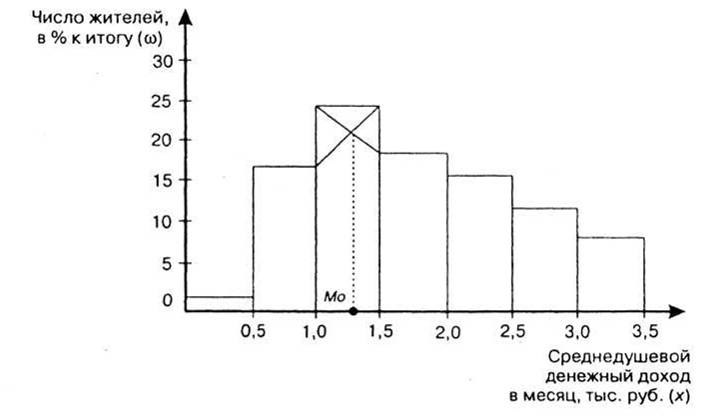
Гистограмма— столбиковая диаграмма, для построения которой на оси абсцисс откладывают отрезки, равные величине интервалов вариационного ряда. На отрезках строят прямоугольники, высота которых в принятом масштабе по оси ординат соответствует частотам (или частостям) (рис. 4.1).
Для графического изображения дискретного вариационного ряда применяют полигон распределения, для построения которого необходимо соединить прямыми отрезками точки с координатами х, 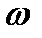
Рис. 4.1. Гистограмма распределения населения
по величине среднедушевого дохода
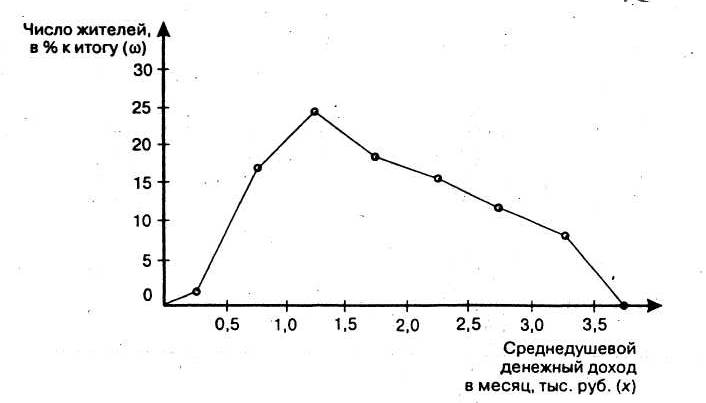
Рис. 4.2. Полигон распределения населения
по величине среднедушевого дохода
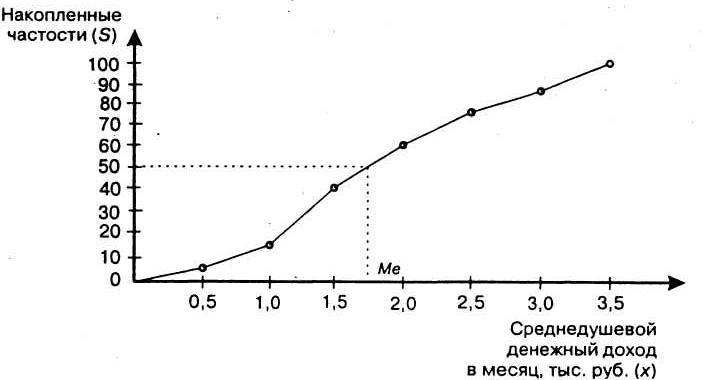
Рис. 4.3. Кумулята распределения населения
по величине среднедушевого дохода
Очевидно, что гистограмма легко может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить отрезками прямых, при этом середины верхних сторон двух крайних прямоугольников соединить с осью абсцисс в точках, отстоящих в принятом масштабе на величину интервалов от середины первого и последнего интервалов.
Кумулятараспределения строится по накопленным частотам (частостям). Накопленные частоты (частости) определяют последовательным суммированием частот (частостей), они показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое значение (гр. 4, табл. 4.1). При построении кумуляты интервального ряда (рис. 4.3) нижней границе первого интервала соответствует нулевая частота (частость), верхней — вся частота (частость) первого интервала. Верхней границе второго интервала — сумма частот (частостей) первого и второго интервалов и т. д. Верхней границе последнего интервала — сумма накопленных частот (частостей) во всех интервалах, что соответствует общей численности изучаемой совокупности или 100 %.
4.3. Показатели центра распределения
и структурные характеристики вариационного ряда
Для характеристики среднего значения признака в вариационном ряду используются так называемые показатели центра распределения. К ним относятся средняя величина признака, мода и медиана.
Расчет средней величины признака( 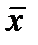
где х — варианты признака;
f — частоты (частости).
При расчете средней величины интервального ряда в качестве вариантов признака используются значения середины интервалов (гр. 5, табл. 4.1). Для нахождения середины открытых интервалов (в нашем примере это первая и последняя группы) необходимо их предварительно условно закрыть, т.е. определить недостающую верхнюю и нижнюю границы. Принято считать, что в первой группе величина интервала равна интервалу второй группы, а в последней — интервалу предыдущей. В рассматриваемом примере используется ряд с равными интервалами, величина которых 0,5 тыс. руб. Тогда условная нижняя граница первого интервала будет равна: 0,5 тыс. руб. – 0,5 тыс. руб. = 0, а середина — 0,25 тыс. руб., условная верхняя граница последнего интервала: 3,0 тыс. руб. + 0,5 тыс. руб. = 3,5 тыс. руб., а середина — 3,25 тыс. руб.
Осуществим расчет средней величины месячного среднедушевого денежного дохода ( 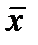
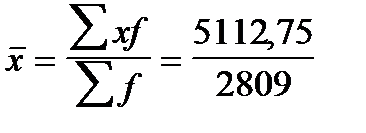
Месячный среднедушевой доход составляет 1820 руб.
Можно при расчете средней величины в качестве весов использовать частости распределения (ω) (промежуточные расчеты в гр. 7 табл. 4.1). Величина средней от этого не меняется.
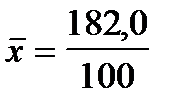
Мода— значение признака, наиболее часто встречающееся в изучаемой совокупности. В дискретном ряду модой является вариант с наибольшей частотой (частостью). В интервальном вариационном ряду мода рассчитывается по формуле:
где 
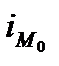
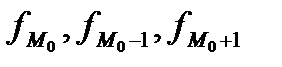
Модальный интервал — это интервал, имеющий наибольшую частоту (частость). В нашем примере это третий интервал — от 1,0 до 1,5 тыс. руб.
Рассчитаем модальное значение признака, используя в качестве весов частости распределения:
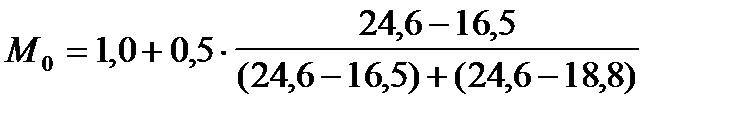
Таким образом, в нашем примере наиболее часто встречающаяся величина среднедушевого дохода составляет 1 290 руб.
Расчет моды с использованием в качестве весов частот распределения даст аналогичный результат:
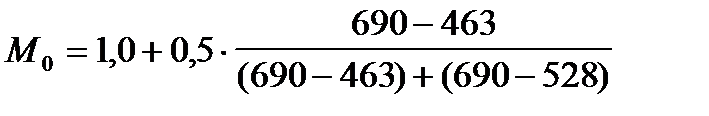
Отметим, что вычисление моды в интервальном ряду является весьма условным.
Приближенно модальное значение признака можно определить и графически — по гистограмме. Для этого нужно взять столбец, имеющий наибольшую высоту, и из его левого верхнего угла провести отрезок в верхний угол последующего столбца, а из правого угла — в верхний правый угол предыдущего (см. рис. 4.1). Абсцисса точки пересечения отрезков и будет соответствовать модальному значению признака в изучаемой совокупности.
Медиана — вариант, расположенный в середине упорядоченного вариационного ряда, делящий его на две равные части, таким образом, что половина единиц совокупности имеют значения признака меньше, чем медиана, а половина — больше, чем медиана. В интервальном ряду медиана определяется по формуле:
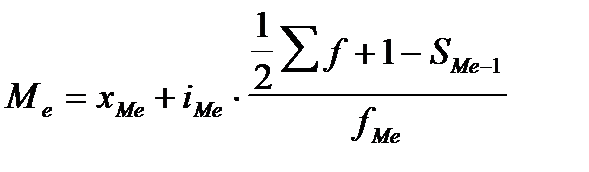
где хMe — начало медианного интервала; iMe — величина медианного интервала;
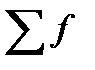
fM —— частота (частость) медианного интервала;
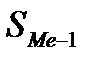
Медианный интервал — это интервал, в котором находится порядковый номер медианы. Для его определения необходимо подсчитать сумму накопленных частот (частостей) до числа, превышающего половину объема совокупности. По данным гр. 4 табл. 4.1 находим интервал, сумма накопленных частот в котором превышает 50 %. Это интервал от 1,5 до 2,0 тыс. руб. (S = 60,8 %), он и является медианным. Тогда
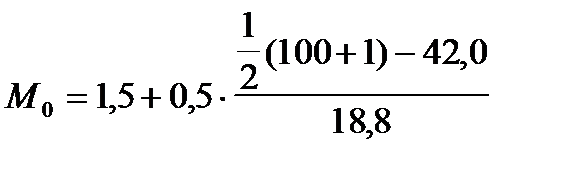
Следовательно, половина жителей города в нашем примере имеет месячный среднедушевой доход меньше 1 720 руб., а половина — больше этой суммы.
Расчет медианного значения по частостям распределения даст аналогичный результат:
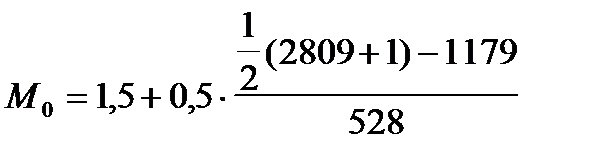
где 1 179 —сумма накопленных частот в домедианном интервале.
Медиану приближенно можно определить графически — по кумуляте. Для этого высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения и является медианой (см. рис. 4.3).
Расчет модального и медианного значений для вариационных рядов с неравными интервалами осуществляется по формулам, аналогичным приведенным выше, только вместо показателей частот (частостей) используются показатели абсолютной или относительной плотности распределения, которые обеспечивают сопоставимость неравных интервалов. Показатели плотности распределения находятся как отношения частот (частостей) к величине интервала:
– абсолютная плотность распределения
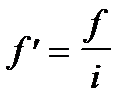
– относительная плотность распределения
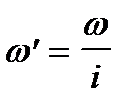
где i — величина интервала.
По соотношению характеристик центра распределения (средней величины, моды и медианы) можно судить о симметричности эмпирического ряда распределения. Симметричным является распределение, в котором частоты двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. В симметричном распределении средняя величина, медиана и мода равны между собой:
Если 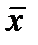
Соотношение 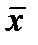
При анализе вариационного ряда важно знать не только направление асимметрии (правосторонняя или левосторонняя), но и ее степень, которая измеряется с помощью коэффициентов асимметрии.
Моду и медиану называют еще структурными средними, поскольку они дают количественную характеристику структуры строения вариационных рядов. К структурным характеристикам относятся и другие порядковые статистики: квартили — делящие, ряд на 4 равные части, децили — делящие ряд на 10 частей, перцинтили — на 100 частей и др.
Дата добавления: 2016-05-16 ; просмотров: 5159 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Вариационные ряды, их виды. Графическое изображение вариационных рядов



Вариациейназывается различие значений признака у отдельных единиц изучаемой совокупности в один и тот же период или момент времени.
Статистический анализ вариации предполагает:
1. Построение вариационного ряда
2. Графическое изображение вариационного ряда
3. Расчет основных характеристик вариационного ряда.
Построение вариационного ряда (ряд распределения) – это упорядоченное распределение единиц совокупности по возрастающим или убывающим значениям признака.
В составе любого вариационного ряда можно выделить три основных элемента: варианта, частота и частость.
Варианта– это значения, которые принимает исследуемый признак и обозначается через x.
Частоты вариационного ряда – абсолютная численность отдельных групп с различными значениями признака, обозначается через m.
Частости вариационного ряда – удельные веса (доли) отдельных групп в общей совокупности.
Вариационные ряды бывают двух видов:
В дискретных рядах варианты представлены в виде целочисленных величин. Если варианты представлены в виде интервалов, то такие ряды называются интервально-вариационными.
Для анализа вариационных рядов и определения формы распределения используются графики. При графическом изображении вариационного ряда в статистике используется полигон распределения, гистограмма и кумулята.
Чтобы построить полигон распределения на оси абсцисс отмечают точки, соответствующие величине вариант значений признака из них восстанавливаются перпендикуляры, длине которых соответствует частота этих вариант по принятому масштабу на оси ординат. Вершины перпендикуляров соединяются отрезками прямой.
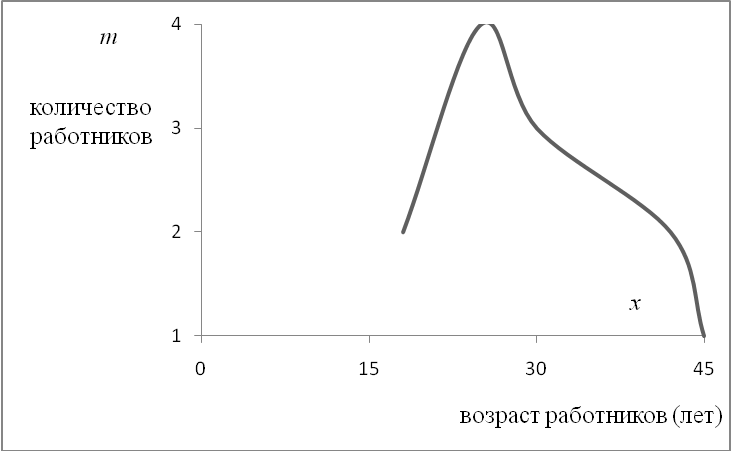
Графическое изображение дискретного ряда, приведенного в таблице 4.2, глава «Средние величины») представлено на рис. 5.1.
Рис. 5.1. Полигон распределения работников по возрасту
Для графического изображения интервального ряда используется гистограмма.
Гистограмма – столбиковая диаграмма, для построения которой на оси абсцисс откладываются отрезки, равные величине интервалов вариационного ряда. На отрезках строят прямоугольники, высота которых в принятом масштабе по оси ординат соответствует частотам или частостям. Графическое изображение интервально-вариационного ряда, приведенного в таблице 4.3 (глава 4, «Средние величины») представлено на рис. 5.2.
| х |
| 5 10 15 Mо 20 25 30 35 |
| Количество работников |
| m |
| Заработная плата, тыс. руб. |
Рис. 5.2. Гистограмма распределения работников по величине заработной платы
По гистограмме можно определить показатель центра распределения – моду (М0), который будет рассмотрен далее.
Кумулята – распределение строится по накопленным частотам, они определяются последовательным суммированием частот.
Накопленные частоты показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение.
Накопленные частоты по рассматриваемому предыдущему примеру (таб. 4.3) будут равны:
1 группа (до 10 тыс. руб.) – 2;
2 группа (от 10-15) – 10;
3 группа (от 15-20) – 25;
4 группа (от 20-25) – 35;
5 группа (от 25-30) – 41;
6 группа (свыше 30) – 45.
Кумулята распределения работников по заработной плате представлена на рис. 5.3.
| Ме |
| 0 7,5 12,5 17,5 22,5 27,5 32,5 |
| x |
| m |
Рис. 5.3. Кумулята распределения работников по заработной плате
По кумуляте можно определить еще один показатель центра распределения – медиану (Ме).
Графическое изображение рядов распределения: полигон, гистограмма. Показатели центра распределения, колеблемости признака. Формы распределения.
Поможем написать любую работу на аналогичную тему
Графики являются наглядной формой отображения рядов распределения. Для изображения рядов применяются линейные графики и плоскостные диаграммы, построенные в прямоугольной системе координат.
Для графического представления атрибутивных рядов распределения используются различные диаграммы: столбиковые, линейные, круговые, фигурные, секторные и т. д.
Для дискретных вариационных рядов графиком является полигон распределения.
Полигоном распределения называется ломаная линия, соединяющая точки с координатами 




График строится в принятом масштабе. Вид полигона распределения приведен на рис. 5.1.
При построении графиков рядов распределения большое значение имеет соотношение масштабов по оси абсцисс и оси ординат. В этом случае и необходимо руководствоваться «правилом золотого сечения», в соответствии с которым высота графика должна быть примерно в два раза меньше его основания.
При проведении эмпирического исследования ряда распределения рассчитываются и анализируются следующие группы показателей:
• показатели положения центра распределения;
• показатели степени его однородности;
• показатели формы распределения.
Показатели положения центра распределения. К ним относятся степенная средняя в виде средней арифметической и структурные средние – мода и медиана.
Средняя арфметическая для дискретного ряда распределения рассчитывается по формуле:
В отличие от средней арифметической, рассчитываемой на основе всех вариант, мода и медиана характеризует значение признака у статистической единице, занимающей определенное положение в вариационном ряду.
Медиана (Me) — значение признака у статистической единицы, стоящей в середине ранжированного ряда и делящей совокупность на две равные по численности части.
Медиану используют как наиболее надежный показатель типичного значения неоднородной совокупности, так как она нечувствительна к крайним значениям признака, которые могут значительно отличаться от основного массива его значений. Кроме этого, медиана находит практическое применение вследствие особого математического свойства: 
Данные приведены в таблице 5.2.
Мода выбирается по максимальному значению частоты: при nmax = 14 Mo=4, т.е. чаще всего встречается 4-ый разряд. Для нахождения медианы Me определяются центральные единицы 
Мода определяется следующим образом:
• По максимальному значению частоты определяется интервал, в котором находится значение моды. Он называется модальным.
• Внутри модального интервала значение моды вычисляется по формуле:
Для расчета медианы в интервальных рядах используется следующий подход:
• По накопленным частотам находится медианный интервал. Медианным называется интервал, содержащий центральную единицу.
• Внутри медианного интервала значение Me определяется по формуле:
В неравноинтервальных рядах при вычислении Mo используется другая частотная характеристика – абсолютная плотность распределения:
Расчет моды и медианы для интервального ряда распределения рассмотрим на примере ряда распределения рабочих по стажу, приведенного в таблице 5.3.
• Максимальная частота n max = 13, она соответствует четвертой группе, следовательно, модальным является интервал с границами 12 – 16 лет.
• Моду рассчитаем по формуле:
Чаще всего встречаются рабочие со стажем работы около 13 лет. Мода не находится в середине модального интервала, она смещена к его нижней границе, связано это со структурой данного ряда распределения (частота предмодального интервала значительно больше частоты постмодального интервала).
• По графе накопленных частот определяется медианный интервал. Он содержит 25 и 26-у статистические единицы, которые находятся в разных группах – в 3-ей и 4-ой. Для нахождения Me можно использовать любую из них. Расчет проведем по 3-ей группе:
Такое же значение Me можно получить при её расчете по 4-ой группе:
Для нахождения моды в интервальном ряду правую вершину модального прямоугольника нужно соединить с правым верхним углом предыдущего прямоугольника, а левую вершину – с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.
Для определение медианы высоту наибольшей ординаты кумуляты, соответствующей общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой.
Кроме Mo и Me в вариантных рядах могут быть определены и другие структурные характеристики – квантили. Квантили предназначены для более глубокого изучения структуры ряда распределения. Квантиль – это значение признака, занимающее определенное место в упорядоченной по данному признаку совокупности. Различают следующие виды квантилей:
• квартили 
• децили 
Рассчитаем квартили для ряда распределения рабочих участка по стажу работы:
Следовательно, у четверти рабочих стаж менее 7 лет и у четверти – более 16 лет. Таким образом, для характеристики положения центра ряда распределения можно использовать 3 показателя: среднее значение признака, мода, медиана.
При выборе вида и формы конкретного показателя центра распределения необходимо исходить из следующих рекомендаций:
• для устойчивых социально-экономических процессов в качестве показателя центра используют среднюю арифметическую. Такие процессы характеризуются симметричными распределениями, в которых
• для неустойчивых процессов положение центра распределения характеризуется с помощью Mo или Me. Для асимметричных процессов предпочтительной характеристикой центра распределения является медиана, поскольку занимает положение между средней арифметической и модой.
Вторая важнейшая задача при определении общего характера распределения – это оценка степени его однородности. Однородность статистических совокупностей характеризуется величиной вариации (рассеяния) признака, т.е. несовпадением его значений у разных статистических единиц. Для измерения вариации в статистике используются абсолютные и относительные показатели. Выяснение общего характера распределения предполагает не только оценку степени его однородности, но и исследование формы распределения, т.е. оценку симметричности и эксцесса.
Из математической статистики известно, что при увеличении объема статистической совокупности 

В статистике различают следующие виды кривых распределения:
• одновершинные кривые; • многовершинные кривые.
Однородные совокупности описываются одновершинными распределениями. Многовершинность распределения свидетельствует о неоднородности изучаемой совокупности или о некачественном выполнении группировки.
Одновершинные кривые распределения делятся на симметричные, умеренно асимметричные и крайне асимметричные.
Распределение называется симметричным, если частоты любых 2-х вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. В таких распределениях
Для характеристики асимметрии используют коэффициенты асимметрии.
Наиболее часто используются следующие из них:
• Коэффициент асимметрии Пирсона
Рис. 5.4.Правосторонняя асимметрия Рис. 5.5. Левосторонняя асимметрия
Чем ближе по модулю As к 1, тем асимметрия существеннее:
Коэффициент асимметрии Пирсона характеризует асимметрию только в центральной части распределения, поэтому более распространенным и более точным является коэффициент асимметрии, рассчитанный на основе центрального момента 3-его порядка:
Центральным моментом в статистике называется среднее отклонение индивидуальных значений признака от его среднеарифметической величины.
Центральный момент k-ого порядка рассчитывается как:
Соответственно формулы для определения центрального момента третьего порядка имеют следующий вид:
Для оценки существенности рассчитанного вторым способом коэффициента асимметрии определяется его средняя квадратическая ошибка:
Для одновершинных распределений рассчитывается еще один показатель оценки его формы – эксцесс. Эксцесс является показателем островершинности распределения. Он рассчитывается для симметричных распределений на основе центрального момента 4-ого порядка
При симметричных распределениях Ех=0. если Ех>0, то распределение относится к островершинным, если Ех