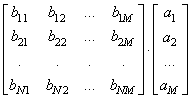
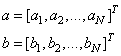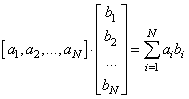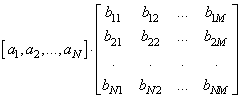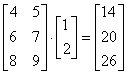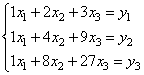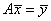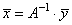Перемножение матриц, не используя встроенных модулей
Решение
Здравствуйте,задача в общем такая. Мне нужно сделать перемножение матриц,которые задает пользователь.Все это должно быть в 1 функции не используя numpy. Прошу помочь. Вот 2 функции, одна запрашивает ввод матрицы,вторая перемножение. Как это соединить что б работала. Прошу помощи.
Добавлено через 15 часов 29 минут
Додумался сам,вроде считает правильно.
Перемножение матриц
Коллеги, всем хорошего вечера:) Требуется помощь в решении следующей задачи: составил матрицу.
Перемножение матриц используя Datagridview
Добрый день. Работаю с C# Windows Forms. Нужна помощь, чтобы разобраться. Есть 3 datagridview.
Параллельное перемножение многомерных матриц с используя CUDA
Здравствуйте. Подскажите как реализовать программный код для перемножения многомерных матриц, чтобы.
Перемножение матриц, умножение матриц на вектор, сложение матриц
Помогите пожалуйста написать программу, которая производит основные действия с матрицами.
Возведение матриц в степени, перемножение и сложение матриц
Даны 3-ех элементные вещественные векторы x и y и квадратные матрицы A и B. Вычислить: (A 2 * x.
Перемножение матриц.
Нужен код для перемножения матрицы и столбца за минимально возможное время. Порядок матрицы ( и.
Перемножение матриц
Пусть есть процедура procedure Peremnozhenie(а1, а2: Matr; var а: Matr; n: integer); var i.
Произведение матриц и векторов, элементы линейной алгебры
Пришло время познакомиться с одной из фундаментальных возможностей пакета NumPy–матричных и векторных вычислений. На одном из прошлых занятий мы с вами уже видели, как можно поэлементно умножать один вектор на другой или одну матрицу на другую:
В консоли увидим результат:
array([[ 10, 22, 36],
[ 52, 70, 90],
[112, 136, 162]])
Матричное умножение
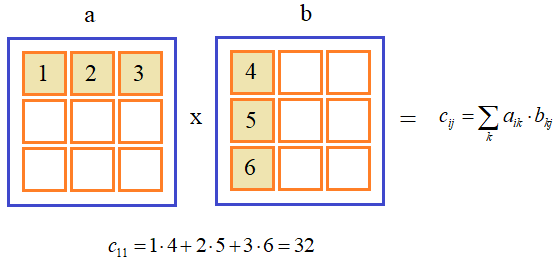
Но если нам нужно выполнить именно матричное умножение, то есть, строки одной матрицы умножать на столбцы другой и результаты складывать:
то для этого следует использовать специальные функции и операторы. Начнем с функций. Итак, чтобы перемножить две матрицы a иbпо всем правилам математики, запишем следующую команду:
Эта функция возвращает новую матрицу (двумерный массив) с результатом умножения:
array([[ 84, 90, 96],
[201, 216, 231],
[318, 342, 366]])
Тот же результат можно получить и с помощью функции:
Считается, что этот вариант предпочтительнее использовать при умножении матриц.
Векторное умножение
Аналогичные операции можно выполнять и с векторами. Математически, если у нас имеются два вектора:
то их умножение можно реализовать в двух видах:
Первое умножение реализуется либо через функцию:
Либо, более предпочтительной функцией для внутреннего умножения векторов:
Второй вариант умножения (внешнее умножение векторов) реализуется с помощью функции:
получим результат в виде следующей матрицы:
array([[1., 1., 1., 1., 1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5., 5., 5., 5., 5.],
[6., 6., 6., 6., 6., 6., 6., 6., 6.],
[7., 7., 7., 7., 7., 7., 7., 7., 7.],
[8., 8., 8., 8., 8., 8., 8., 8., 8.],
[9., 9., 9., 9., 9., 9., 9., 9., 9.]])
Операция умножения матриц и векторов используется довольно часто, поэтому в пакете NumPy имеется весьма полезный перегруженный оператор, заменяющий функцию matmul:
или, с использованием матриц:
Умножение вектора на матрицу
Наконец, рассмотрим умножение вектора на матрицу. Это также можно записать двумя способами:
Для реализации первого способа, зададим одномерный вектор и двумерную матрицу:
И, затем, воспользуемся уже знакомой нам функцией dot:
При такой записи, когда одномерный массив записан первым аргументом, а матрица – вторым, получаем умножение вектора-строки на матрицу, то есть, первый способ.
Для реализации второго способа аргументы нужно поменять местами: сначала указать матрицу, а затем, вектор. Но, если мы сейчас это сделаем с нашими массивами, то получим ошибку:
Дело в том, что массив a должен представлять вектор длиной два элемента, так как матрица b имеет размер в 3 строки и 2 столбца:
Определим массивa в два элемента и умножим на матрицу b:
Получаем вектор-строку (одномерный массив) как результат умножения. Обратите внимание, по правилам математики вектор aдолжен быть вектором-столбцом, то есть, быть представленным в виде:
Но мы использовали вектор-строку. В NumPyтак тоже можно делать и это не приведет к ошибке. Результат будет именно умножение матрицы как бы на вектор-столбец. Ну а если использовать вектор-столбец, то и на выходе получим вектор-столбец:
Этого же результат можно достичь, используя оператор @ (перегрузка функции matmul):
Результат будет тем же. Вот так в NumPyвыполняется умножение матриц, векторов и вектора на матрицу.
Элементы линейной алгебры
Из высшей математики хорошо известно, что матрицы можно использовать для решения систем линейных уравнений. Для этого в NumPyсуществует модуль linalg. Давайте рассмотрим некоторые из его функций.
Предположим, имеется квадратная матрица 3×3:
Первым делом вычислим ранг этой матрицы, чтобы быть уверенным, что она состоит из линейно независимых строк и столбцов:
Если ранг матрицы совпадает с ее размерностью, значит, она способна описывать систему из трех независимых линейных уравнений. В нашем случае, система уравнений будет иметь вид:
Здесь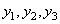 
— некие числа линейного уравнения. Например, возьмем их равными:
Тогда корни уравнения можно вычислить с помощью функции solve:
Другой способ решения этой же системы линейных уравнений возможен через вычисление обратной матрицы. Изначально, уравнение можно записать в векторно-матричном виде:
Откуда получаем решения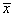 
:
На уровне пакета NumPy это делается так:
Конечно, я здесь представил лишь примеры использования модуля linalg. Приводить все функции нет смысла, так как они имеют довольно специализированное назначение и специалисты в своих областях без труда смогут ими воспользоваться. Для полноты картины я лишь приведу список наиболее характерных функций, чтобы вы знали возможности расширения linalg.
Конечно, это не все математические функции пакета NumPy. Полное описание смотрите на сайте с официальной документацией:
Видео по теме
#2. Основные типы данных. Создание массивов функцией array() | NumPy уроки
#3. Функции автозаполнения, создания матриц и числовых диапазонов | NumPy уроки
#4. Свойства и представления массивов, создание их копий | NumPy уроки
#5. Изменение формы массивов, добавление и удаление осей | NumPy уроки
#6. Объединение и разделение массивов | NumPy уроки
#7. Индексация, срезы, итерирование массивов | NumPy уроки
#8. Базовые математические операции над массивами | NumPy уроки
#9. Булевы операции и функции, значения inf и nan | NumPy уроки
#10. Базовые математические функции | NumPy уроки
#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy уроки
#12. Множества (unique) и операции над ними | NumPy уроки
#13. Транслирование массивов | NumPy уроки
© 2021 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта
Матрица в Python – основы работы
В этой статье мы познакомим вас с матрицей Python. Каждую операцию матрицы мы будем реализовывать с помощью кода.
Что такое матрица в Python?
Матрица в Python – это прямоугольный двумерный массив, в котором данные хранятся в строках и столбцах. Матрица может хранить данные любого типа, такие как числа, строки, выражения и т. д. Мы должны ознакомиться с основными концепциями матрицы перед ее использованием.
Данные расположены по горизонтали, называемые строками, а по вертикали – столбцами. Количество элементов внутри матрицы равно (R) X (C), где R – строки, а C – столбцы. Python не имеет встроенного типа для матриц, поэтому мы будем использовать несколько списков в качестве матриц.
Мы изучим следующие операции, которые применяются к матрицам:
Работа матриц
Приведенная ниже матрица имеет размер 2×2, что означает, что у нее две строки и два столбца.
Создание матрицы в Python
Мы можем создать матрицу на Python, используя вложенный список. Все элементы заключаются в квадратные скобки ([]) и разделяются запятой. Посмотрим на следующие примеры:
Чтение матричных данных
Прочитаем каждую строку определенной матрицы.
В следующем примере мы прочитаем последний элемент каждой строки с помощью программы Python.
В приведенном выше коде мы создали матрицу и получили длину матрицы. Мы повторили каждую строку, используя цикл for, и напечатали результат. Можно прочитать любую строку или столбец, используя вышеуказанный метод.
Давайте разберемся со следующей работой матрицы.
Добавление двух матриц
Мы добавим две матрицы и, используя вложенный цикл for, пройдемся по заданным матрицам.
Умножение двух матриц
Умножение двух матриц такое же, как в приведенном выше коде, только нужно изменить оператор + на *.
Транспонирование матрицы
Транспонирование – это операция, при которой строка данной матрицы преобразуется в столбец и наоборот. Рассмотрим на примере.
В приведенном выше коде у нас есть два цикла for для перебора каждой строки и каждого столбца. Как мы видим, в приведенном выше выводе мы присвоили mat1 [i] [j] и res [j] [k].
Транспонирование с помощью списка
Мы можем использовать значение списка, чтобы транспонировать матрицу с одной строкой кода.
Результат такой же, как и выше. Значение списка сократило количество строк кода и транспонировало матрицу.
Получение матричного ввода от пользователя
До сих пор мы обсуждали предварительно определенные матрицы. Но что, если пользователь хочет ввести свои данные. Итак, разберем следующий пример пользовательской матрицы.
В приведенном выше коде мы взяли данные пользователя, чтобы ввести количество строк и столбцов. Мы ввели 3 строки и 3 столбца; это означает, что в матрице будет 9 элементов. В цикле for элементы вставляются в пустую матрицу с помощью функции append(). Второй цикл for используется для печати входных данных в матричном формате.
Использование функции NumPy и map()
Python предоставляет внешнюю библиотеку NumPy. Она используется для научных вычислений; мы изучим NumPy с матрицей в разделе ниже и используем ее для матрицы пользовательского ввода.
Пример: Создание матрицы с использованием библиотеки NumPy
Библиотека NumPy помогает нам работать с массивом. Чтобы работать с NumPy, нам нужно установить ее, используя следующую команду.
После успешной установки мы должны импортировать ее в нашу программу.
Давайте разберемся в следующем примере.
Работа с матрицей с помощью NumPy
Мы можем выполнять все операции с матрицей, используя numpy.array(), такие как сложение, вычитание, транспонирование, нарезание матрицы и т. д.
Добавление матрицы
Мы создадим две матрицы с помощью функции numpy.array() и добавим их с помощью оператора +. Давайте разберемся в следующем примере.
Умножение
Мы будем использовать метод numpy.dot() для умножения обеих матриц. Это точечное умножение матриц mat1 и mat2, обрабатывает 2D-массив и выполняет умножение.
Нарезка элементов
Мы можем разрезать элемент матрицы, как в стандартном списке Python. Нарезка возвращает элемент на основе индекса начала / конца. Мы также можем сделать отрицательную нарезку. Синтаксис приведен ниже.
Arr представляет имя матрицы. По умолчанию начальный индекс равен 0, например – [: 3], это означает, что начальный индекс равен 0. Если мы не предоставим конечное значение, он будет учитывать длину массива. Мы можем передавать отрицательные значения индекса как в начало, так и в конец. В следующем примере мы применим нарезку в обычном массиве, чтобы понять, как она работает.
Теперь мы реализуем нарезку по матрице. Для выполнения следуйте синтаксису ниже.
Mat1 [row_start: row_end, col_start: col_end]
В приведенном выше синтаксисе:
Мы будем выполнять нарезку в приведенной ниже матрице.
В приведенном выше примере мы напечатали первую и вторую строки и нарезали первый, второй и третий столбцы. Согласно синтаксису нарезки мы можем получить любые строки и столбцы.
Пример – печать первой строки и всех столбцов:
Пример – печать строк матрицы:
Заключение
До сих пор мы обсуждали базовую матрицу с использованием Python. Матрица Python – это специализированный двумерный прямоугольный список данных. Она может состоять из чисел, строк, выражения, символов и т. д. Python не предоставляет прямого способа реализации матричного типа данных. Мы можем создать матрицу, используя вложенный список и библиотеку NumPy.
Умножение матриц
Напишите программу, вычисляющую произведение матриц. При этом исходные матрицы и матрица продукт находятся в файлах, в программе может храниться только по одному элементу каждой из матриц. После проведения расчётов выведите результат.
Туплю, помогите, пожалуйста. Я не очень хорошо понимаю, как питон взаимодействует с файлами.
Умножение матриц
Здравствуйте, почему при умножении этих двух матриц мне выводит одно число, если в итоге должна.
Упростить код для программы «сложение и умножение двух матриц»
print(«Программа для сложения и умножения двух матриц») a= b= u= z= w= k=0 q=0 i=0 j=0
Умножение матриц
Здравствуйте! Мне нужно написать программу умножения двух матриц A и B. Я написала функции.
Перемножение матриц, умножение матриц на вектор, сложение матриц
Помогите пожалуйста написать программу, которая производит основные действия с матрицами.
Процедуры. Умножение матриц, векторов. Скалярное умножение. Надо найти ошибку
Дано 6-элементные действительные векторы и квадратные матрицы A,B,C 6-ого порядка. Найти.
Транспонирование, умножение матриц, сложение матриц Реализовать в одной программере
транспонирование, умножение матриц, сложение матриц; B^3-A^T Реализовать в одной программере.
Умножение матриц с интерфейсом и возможность заполнения исходных матриц из файла
Здравствуйте. Я сделал программу, которая умножает матрицы с интерфейсом, только проблема в том что.
Умножение треугольных матриц«Методы обработки разреженных матриц»
Нужно перемножить треугольные матрицы в обычном виде и в свёрнутом. С обычным проблем нет. Доступ.
Умножение матриц (не работает для неквадратных матриц)
Доброго времени суток. Написал код для перемножения двух матриц. При вводе квадратной матрицы всё.
Базовые операции NumPy / np 3
Вы уже знаете, как создавать массив NumPy и как определять его элементы. Теперь пришло время разобраться с тем, как применять к ним различные операции.
Арифметические операторы
Арифметические операторы — первые, которые предстоит использовать. К числу наиболее очевидных относятся прибавление и умножение на скаляр.
Их можно использовать для двух массивов. В NumPy эти операции поэлементные, то есть, они применяются только к соответствующим друг другу элементам. Это должны быть объекты, которые занимают одно и то же положение, так что результатом станет новый массив, содержащий итоговые величины в тех же местах, что и операнды.
И даже в случае с многомерными массивами можно применять арифметические операторы поэлементно.
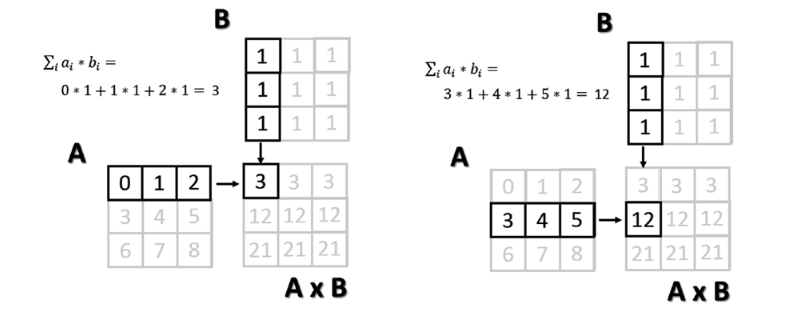
Произведение матриц
Каждый элемент результирующей матрицы — сумма произведений каждого элемента соответствующей строки в первой матрице с соответствующим элементом из колонки второй. Рисунок ниже показывает процесс произведения матриц (для двух элементов).
Но поскольку произведение матриц — это не коммутативная операция, порядок операндов имеет значение. В данном случае A*B не равняется B*A.
Операторы инкремента и декремента
Таким образом использование этих операторов дает возможность получать более масштабные результаты, чем в случае с обычными операторами инкремента, увеличивающими значения на один. Их можно использовать в самых разных ситуациях. Например, они подходят для изменения значений без создания нового массива.
Универсальные функции (ufunc)
Многие функции уже реализованы в библиотеке NumPy.