Слово Высказывание истинно как пишется - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

2. Высказанное суждение, замечание, мнение. Собрать высказывания классиков марксизма о языке.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

выска́зывание

1. действие по значению гл. высказывать; произнесение слов, говорение

2. результат такого действия, произнесённый текст, сформулированная мысль ◆ Приписываемое мне высказывание во всех своих многочисленных является грубейшей фальшивкой.

3. лог. выражающее суждение утвердительное повествовательное предложение, об истинности или ложности которого можно судить ◆ С точки зрения логики, «Сейчас идёт дождь» — высказывание, а «Давай пойдём обедать» — не высказывание.

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: глазомер — это что-то нейтральное, положительное или отрицательное?

Ассоциации к слову «высказывание&raquo

Синонимы к слову «высказывание&raquo

Предложения со словом «высказывание&raquo

Цитаты из русской классики со словом «высказывание»

Сочетаемость слова «высказывание&raquo

Каким бывает «высказывание»

Понятия, связанные со словом «высказывание»

Отправить комментарий

Дополнительно

Предложения со словом «высказывание&raquo

Подобные высказывания могут показаться вам сказкой, но, когда вы прочтёте главу 10, вы поймёте, как выпускники курсов настраивают свой мозг на регуляцию организма и ускорение естественного выздоровления.

Утешала я себя известным высказыванием культового французского виноградаря – об этом человеке знают все, кто хотя бы немножко соприкоснулся с виноградарством.

Значит, последнее высказывание словаря не имеет никакого отношения к определению понятия души, но оно им пользуется, заимствуя из первого.

Источник

Любое ли высказывание истинно?

Рассмотрим, любое ли высказывание истинно?

Найдём точку опоры, допустим, что все мысли приходят к человеку из информационного поля, то есть они все должны быть истинны. Возможно ли, такое или нет? Возьмем неправильное высказывание, например: «Кошка – это петух». Казалось бы это глупость. С точки зрения логики физического мира это так. А если взглянуть глубже. Чем мы руководствуем, когда сравниваем понятие кошка и понятие петух? Внешним видом, способностями, питанием, строением тела. То есть тем, что мы видим или можем видеть. А если сравнить их с точки зрения строения их тел на атомном уровне. И кошка, и петух состоят из атомов. Основа строения у всех атомов одна. Следовательно, можно сказать, что кошка – это петух с точки зрения атомного строения.

Возьмём другое утверждение, например «Луна больше Солнца». Опять глупость. Установлено, что Солнце гораздо больше Луны, хотя, когда мы их видим на небе они почти одного и того же размера. А если взглянуть глубже. Рассмотрим их во времени. Со временем Солнце может превратиться в белого карлика, то есть, возможно, стать меньше Луны. Будем считать, что её размеры не изменяться, такое вполне вероятно. Получаем, что на определённом отрезке времени высказывание «Луна больше Солнца» истинно.

Чтобы понять истинность любого высказывания, нужно посмотреть на него с разных точек зрения и во времени. Оно может быть истинно на определённом этапе и для определённых условий, а для всего остального ложно.

Является истиной то, что я написала или нет? Думаю и на это надо посмотреть с различных точек зрения и во времени. То есть попытаться расширить своё сознание, изменив логику мышления.

Источник

Логическое высказывание

Логическое высказывание

Логическое высказывание — утверждение, которому всегда можно поставить в соответствие одно из двух логических значений: ложь (0, ложно, false) или истина (1, истинно, true). Логическое высказывание принято обозначать заглавными латинскими буквами. Высказывательной формой называется логическое высказывание, в котором один из объектов заменён переменной. При подстановке вместо переменной какого-либо значения высказывательная форма превращается в высказывание.

Пример: A(x) = «В городе x идет дождь.» A — высказывательная форма, x — объект.

Отрицание логического высказывания — логическое высказывание, принимающее значение «истинно», если исходное высказывание ложно, и наоборот.

Конъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны.

Дизъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно.

Импликация двух логических высказываний A и B — логическое высказывание, ложное только тогда, когда B ложно, а A истинно.

Равносильность (эквивалентность) двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны.

Кванторное логическое высказывание с квантором всеобщности (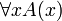) — логическое высказывание, истинное только тогда, когда для каждого объекта x из заданной совокупности высказывание A(x) истинно.

Кванторное логическое высказывание с квантором существования (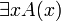) — логическое высказывание, истинное только тогда, когда в заданной совокупности существует объект x, такой, что высказывание A(x) истинно.

См. также

Полезное

Смотреть что такое «Логическое высказывание» в других словарях:

Высказывание (логика) — У этого термина существуют и другие значения, см. Высказывание. Высказывание термин математической логики, обозначающий формализованную структурированную запись мысли с помощью буквенных символов и логических связок, рассматриваемую с точки … Википедия

ЛОГИЧЕСКОЕ СЛЕДСТВИЕ — суждение (предложение, высказывание, формула), логически вытекающее (или, иначе, логически следующее) из посылок умозаключения (или из посылок вывода, состоящего из ряда умозаключений), т.е. выводимое из посылок на основе правил и законов логики … Философская энциклопедия

логическое следование — отношение, существующее между посылками и обоснованно выводимыми из них заключениями. Л.с. относится к числу фундаментальных, исходных понятий логики, точного универсального определения не имеет; в частности, описание его с помощью слов выводимо … Словарь терминов логики

Логическое мышление — Логика (др. греч. λογική «наука о рассуждении», «искусство рассуждения» от λόγος «речь», «рассуждение») наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Поскольку это… … Википедия

логическое следствие — суждение (предложение, высказывание, формула), полученное посредством дедуктивного рассуждения из некоторых исходных суждений. * * * ЛОГИЧЕСКОЕ СЛЕДСТВИЕ ЛОГИЧЕСКОЕ СЛЕДСТВИЕ, суждение (предложение, высказывание, формула), полученное посредством… … Энциклопедический словарь

ЛОГИЧЕСКОЕ СЛЕДСТВИЕ — из данного множества посылок высказывание, являющееся истинным при любой интерпретации нелогич. символов (т. е. имен объектов, функций, предикатов), при к рой истинны посылки. Если высказывание Аявляется Л. с. из множества высказываний Г, то… … Математическая энциклопедия

Логическое следствие — суждение (предложение, высказывание, формула), логически вытекающее (или, иначе, логически следующее) из посылок умозаключения (или из посылок вывода, состоящего из ряда умозаключений), т. е. выводимое из посылок на основе правил и… … Большая советская энциклопедия

БЕСКОНЕЧНОЕ ЛОГИЧЕСКОЕ — понятие диалектической логики, введенное грузинским философом С.Б. Церетели (1907 1966). Б. Л., по определению Церетели, «есть то, отрицание чего утверждает его же. Точнее: это есть утверждение чего либо отрицанием его же». Так, говоря, что нет… … Новейший философский словарь

Источник

Высказывание истинно как пишется

Войти

Авторизуясь в LiveJournal с помощью стороннего сервиса вы принимаете условия Пользовательского соглашения LiveJournal

Проект «логика для чайников». Параграф 38

Доказанное и истинное, ложное и опровергнутое. как это все соотносится друг с другом?

Доказанное

Доказанным называют утверждение, которое выводится из аксиом по “правилам вывода”. Аксиомы считаются доказанными изначально. В применении к повседневности это значит, что у людей есть какие-то “точки соприкосновения”, какие-то вопросы, по которым они изначально уже согласны между собой – это своего рода “аксиомы”. Далее люди пытаются достичь согласия по спорным вопросам, строя доказательства с опорой на “аксиомы”. Вопрос о том, как были доказаны сами аксиомы (и были ли доказаны вообще) остается за кадром.

Истинным называют утверждение, которое удовлетворяет некоторому “критерию истинности”. В серии “логика для чайников” я предлагаю свой критерий, который мне кажется не слишком идеологичным и достаточно универсальным. По нему истиным называются те утверждения, которые соблюдают строгое соответствие между словами и явлениями, которые эти слова должны описать. А соответствие закрепляется в языке – системой соглашений о той, что как называть.

Как связать эти два понятия? Истинное – то, что удовлетворяет критерию. а доказанное – то, что выводится из аксиом. Нам нужен такой “вывод”, чтобы всегда получалось истинное. Для этого надо соблюсти всего два условия:

1. Всякая аксиома должна быть истинной.

2. Всякое “правило вывода” должно выводить из истинного только истинное, всегда.

Если считать логику набором подобных правил, то становится ясно, откуда эта строгость. Стоит один раз допустить немного лжи – ввести ложную аксиому или ввести правило вывода может вывести ложное утверждение – и все, идеальная конструкция разрушается. Однажды допущенная в нее ложь, может распространиться дальше – на выводы.

Одного парадокса Рассела достаточно, чтобы ниспровергнуть “наивную” теорию множеств. Пришлось математикам отказаться от нее и строить новые теории. Хотя, казалось бы, прежняя теория в огромном количестве случаев работала.

Если мы остаемся в пределах двузначной логики, тогда ложными будут все утверждения, которые отрицают истинные. То есть, добавление операции “НЕ” к истинному высказыванию конструирует новое высказывание, которое ложно. И наоборот: добавление операции “НЕ” к ложному высказыванию конструирует новое высказывание, которое истинно. В языке в самом общем случае это реализуется добавлением в начало предложения слов “Неправда, что. ”

Говорят, что высказывание X опровергнуто, если доказано его отрицание НЕ X. Всего то. Опровержением X называется доказательство НЕ X.

Если соблюдать два условия, приведенных выше, то всякое доказанное окажется истинным, а всякое опровергнутое – ложным.

Истинное, но не доказанное; ложное, но не опровергнутое

Замечу, что обратное необязательно верно: иногда для истинного может не найтись подходящего логического доказательства, а для ложного – опровержения.

Но это еще не конец: помимо логических доказательств есть экспериментальные. Помните: “истина – это называние вещей своими именами”? Не можете доказать словами, поставьте эксперимент и убедитесь. А если не можете поставить эксперимент. тогда с чего вы взяли, что имеете дело с истиной? “Жопой чую” – не аргумент.

Не ложное и не истинное

Даже в двузначной логике не про всякое высказывание можно с уверенностью сказать, что оно ложно, или истинно. Есть еще такие, для которых в какой-то момент истинность еще не установлена. Например, истинно или ложно (X И Y)? Это зависит от X и от Y. Пока не выясним, не узнаем, истинность (X И Y).

Непознанное, неизвестное, недоказанное

Такое состояние неопределенности – это вовсе не третье значение истинности. Значений истинности по-прежнему два. Это одно из состояний для нашего знания об истинности. Может быть:

1. знаем, что истинное
2. знаем, что ложное
3. не знаем, истинно или ложно

Третье состояние “незнания” может иметь бесконечное число вариантов. В том примере есть X, и есть Y. Если мы узнаем про X, это еще не значит, что мы узнаем про Y. Получается, это – разные “незнания”, по одному “незнанию” на каждую переменную (вернее, на каждую “свободную” переменную). В математике есть одно очень красноречивое название для переменных: “неизвестная”. Именно так – не известно, не знаю.

Первое состояние (аналогично и второе) тоже допускает варианты. Откуда мы знаем, что нечто истинно? Может быть, это доказано логически, может, экспериментально, может, и так, и эдак. Опять же, может быть несколько вариантов логических доказательств.

Истинность и смысл

Мы можем говорить об истинности или ложности высказываний, но это еще не все, что содержится в тексте. Истинность – только часть информации. Обычно высказывание несет дополнительные знания о мире. Высказывания “цыпленок желтый” и “трава зеленая” – оба истинны, но говорят о разном. Когда мы указываем истинность, мы “извлекаем” из текста лишь небольшой кусочек – знание о том, насколько текст соответствует явлению.

Я буду использовать символ Tr для того, чтобы обозначать эту операцию извлечения истинности.

Например:
Tr(“трава зеленая”) = true
Tr(“цыпленок зеленый”) = false

Источник

Логическое высказывание

Логическое высказывание

Логическое высказывание — утверждение, которому всегда можно поставить в соответствие одно из двух логических значений: ложь (0, ложно, false) или истина (1, истинно, true). Логическое высказывание принято обозначать заглавными латинскими буквами. Высказывательной формой называется логическое высказывание, в котором один из объектов заменён переменной. При подстановке вместо переменной какого-либо значения высказывательная форма превращается в высказывание.

Пример: A(x) = «В городе x идет дождь.» A — высказывательная форма, x — объект.

Отрицание логического высказывания — логическое высказывание, принимающее значение «истинно», если исходное высказывание ложно, и наоборот.

Конъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны.

Дизъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно.

Импликация двух логических высказываний A и B — логическое высказывание, ложное только тогда, когда B ложно, а A истинно.

Равносильность (эквивалентность) двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны.

Кванторное логическое высказывание с квантором всеобщности (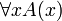) — логическое высказывание, истинное только тогда, когда для каждого объекта x из заданной совокупности высказывание A(x) истинно.

Кванторное логическое высказывание с квантором существования (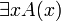) — логическое высказывание, истинное только тогда, когда в заданной совокупности существует объект x, такой, что высказывание A(x) истинно.

См. также

Полезное

Смотреть что такое «Логическое высказывание» в других словарях:

Высказывание (логика) — У этого термина существуют и другие значения, см. Высказывание. Высказывание термин математической логики, обозначающий формализованную структурированную запись мысли с помощью буквенных символов и логических связок, рассматриваемую с точки … Википедия

ЛОГИЧЕСКОЕ СЛЕДСТВИЕ — суждение (предложение, высказывание, формула), логически вытекающее (или, иначе, логически следующее) из посылок умозаключения (или из посылок вывода, состоящего из ряда умозаключений), т.е. выводимое из посылок на основе правил и законов логики … Философская энциклопедия

логическое следование — отношение, существующее между посылками и обоснованно выводимыми из них заключениями. Л.с. относится к числу фундаментальных, исходных понятий логики, точного универсального определения не имеет; в частности, описание его с помощью слов выводимо … Словарь терминов логики

Логическое мышление — Логика (др. греч. λογική «наука о рассуждении», «искусство рассуждения» от λόγος «речь», «рассуждение») наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Поскольку это… … Википедия

логическое следствие — суждение (предложение, высказывание, формула), полученное посредством дедуктивного рассуждения из некоторых исходных суждений. * * * ЛОГИЧЕСКОЕ СЛЕДСТВИЕ ЛОГИЧЕСКОЕ СЛЕДСТВИЕ, суждение (предложение, высказывание, формула), полученное посредством… … Энциклопедический словарь

ЛОГИЧЕСКОЕ СЛЕДСТВИЕ — из данного множества посылок высказывание, являющееся истинным при любой интерпретации нелогич. символов (т. е. имен объектов, функций, предикатов), при к рой истинны посылки. Если высказывание Аявляется Л. с. из множества высказываний Г, то… … Математическая энциклопедия

Логическое следствие — суждение (предложение, высказывание, формула), логически вытекающее (или, иначе, логически следующее) из посылок умозаключения (или из посылок вывода, состоящего из ряда умозаключений), т. е. выводимое из посылок на основе правил и… … Большая советская энциклопедия

БЕСКОНЕЧНОЕ ЛОГИЧЕСКОЕ — понятие диалектической логики, введенное грузинским философом С.Б. Церетели (1907 1966). Б. Л., по определению Церетели, «есть то, отрицание чего утверждает его же. Точнее: это есть утверждение чего либо отрицанием его же». Так, говоря, что нет… … Новейший философский словарь

Источник