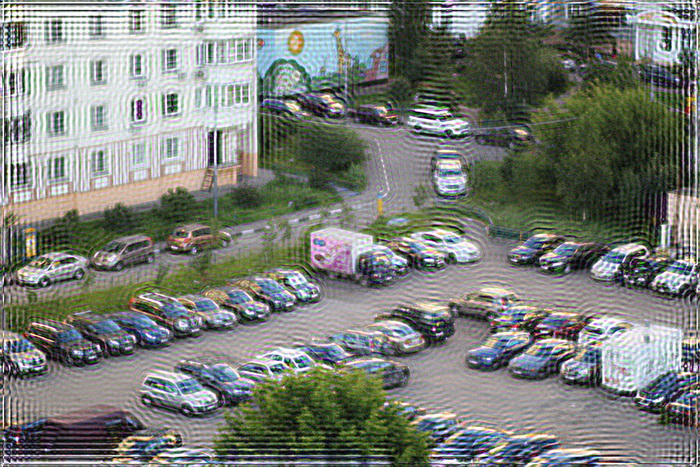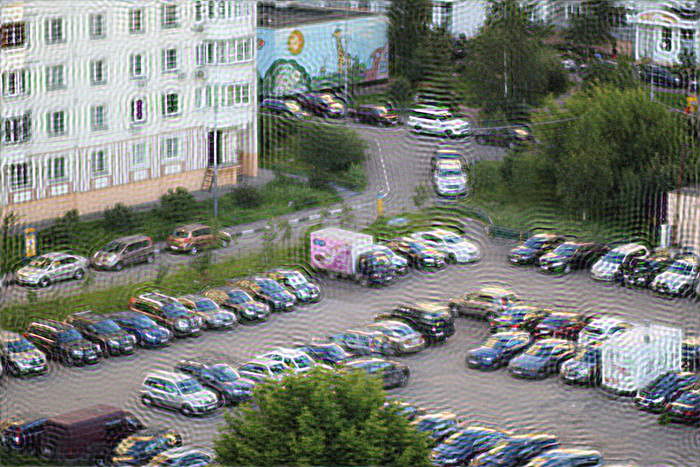Искаженный
Смотреть что такое «Искаженный» в других словарях:
искаженный — См … Словарь синонимов
искаженный — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики защита информации EN distorted … Справочник технического переводчика
искаженный — • неузнаваемо искаженный … Словарь русской идиоматики
искаженный — верный … Словарь антонимов
искаженный — Syn: неправильный, искривленный, перекошенный, исковерканный, изуродованный Ant: правильный, выпрямленный, улучшенный, разглаженный … Тезаурус русской деловой лексики
искаженный — ИСКАЖЁННЫЙ ая, ое. 1. Неправильный, переиначенный, извращённый. Представить факты в искажённом виде. И. русский язык. И ое представление о чём л. 2. Чрезвычайно изменившийся, потерявший обычный, естественный вид (о лице, наружности, голосе).… … Энциклопедический словарь
искаженный канал — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN suffered signal … Справочник технического переводчика
искаженный код — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN mutilated code … Справочник технического переводчика
преднамеренно искаженный — прил., кол во синонимов: 2 • затемненный (27) • предвзято изображенный (2) Словарь синонимов ASIS. В.Н. Тришин. 2 … Словарь синонимов
иррационалистически-искаженный — иррационалистически искаженный … Орфографический словарь-справочник
Как правильно пишется слово искажённый?
Правильный вариант написания слова: искажённый
краткая форма: искажен
Правило
Это слово, которое мы рекомендуем запомнить. Для проверки правильности написания используйте орфографический словарь русского языка, например, под редакцией Д.Н.Ушакова.
Пишем НН:
Важно!
Разъясним отличия причастия и прилагательного:
Морфологический разбор слова искажённый
1. Часть речи — причастие, образовано от глагола исказить
2. Морфологические признаки:
Начальная форма: искажённый (именительный падеж единственного числа мужского рода);
Постоянные признаки: страдательное, прошедшее время, совершенный вид;
Непостоянные признаки: единственное число, именительный падеж, мужской род, полная форма.
3. Синтаксическая роль: Может быть различным членом предложения, смотрите по контексту.
Ударение и состав слова
Ударение падает на слог с буквой ё.
Всего в слове 10 букв, 4 гласных, 6 согласных, 4 слога.
Примеры использования и цитаты
Пусть искаженные черты Он обрисовывает смело,- Ведь разлюбить не сможешь ты, Как полюбить ты не сумела. Любить лишь можно только раз, Вот оттого ты мне чужая, Что липы тщетно манят нас, В сугробы ноги погружая. Ведь знаю я и…
Стихотворение Какая ночь — Есенин С.А., читаем онлайн.
Несколько искаженный, вы все же можете быть узнаны в их описаниях. Он посмотрел на Фирса. Лицо последнего, принадлежащее к числу тех, которых мы забываем тысячами, вздрагивало от волнения. — Торопитесь же…
«Трагедия плоскогорья Суан» — Грин Александр
Но искаженные черты его дышали тогда такой добротой, лихорадочная усмешка на его губах сменялась такой трогательной улыбкой, окруженные тонкими морщинами карие глаза светились такою любовью, что я невольно прижимался…
Проверочное слово к слову «рисунок»
рисунок ресунок рисунак или ресунак
Правильный вариант написания: «рисунок». Слово пишется с гласной буквой «и» в корне и гласной «о» в суффиксе. Проверочного слова к гласной «и» нет.
Правило
В составе существительного «рисунок» выделяется корень «рис», суффикс «ун» и суффикс «ок». Окончание нулевое. Ударение падает на второй слог, поэтому корневая гласная «и» занимает слабую позицию.
Для проверки безударной гласной нужно подобрать однокоренное слово или изменить форму слова так, чтобы сомнительная гласная стала ударной. Гласная буква, стоящая под ударением в корне слова, пишется также и в безударной позиции однокоренного слова.
Падежные формы существительного «рисунок»: «рисунка», «рисунку», «рисунок», «рисунком», о «рисунке». Родственные слова: «рисовать», «рисование», «зарисовка», «рисовальщик» и другие. Во всех однокоренных словах гласная «и» сохраняет безударное положение. Написание гласной «и» в существительном «рисунок» нужно запомнить или смотреть в словаре.
Вторая безударная гласная находится в суффиксе «ок». Написание суффикса «ок» или «ак» зависит от значения слова и ударной позиции. Многозначный суффикс «ак/як» обычно стоит под ударением и образует существительные мужского рода, являющиеся носителями признака, заключенного в мотивирующем слове. Например: «рыбак», «земляк», «чужак», «ветряк», «тесак», «червяк», «гусак». Суффикс «ок» в слове «рисунок» находится в безударной позиции и не относится к данной категории слов. Существительное «рисунок» пишется с гласной буквой «о» в суффиксе «ок».
Пример
На стене висел забавный детский рисунок с изображением лошади.
Восстановление расфокусированных и смазанных изображений. Практика
Не так давно я опубликовал на хабре первую часть статьи по восстановлению расфокусированных и смазанных изображений, где описывалась теоретическая часть. Эта тема, судя по комментариям, вызвала немало интереса и я решил продолжить это направление и показать вам какие же проблемы появляются при практической реализации казалось бы простых формул.
В дополнение к этому я написал демонстрационную программу, в которой реализованы основные алгоритмы по устранению расфокусировки и смаза. Программа выложена на GitHub вместе с исходниками и дистрибутивами.
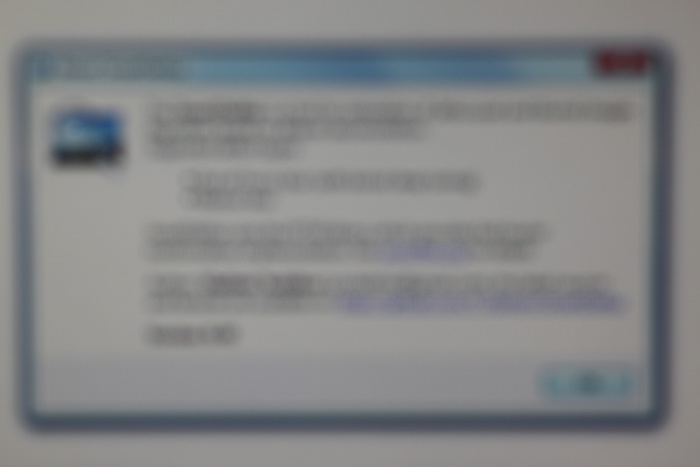
Ниже показан результат обработки реального размытого изображения (не с синтетическим размытием). Исходное изображение было получено камерой Canon 500D с объективом EF 85mm/1.8. Фокусировка была выставлена вручную, чтобы получить размытие. Как видно, текст совершенно не читается, лишь угадывается диалоговое окно Windows 7.
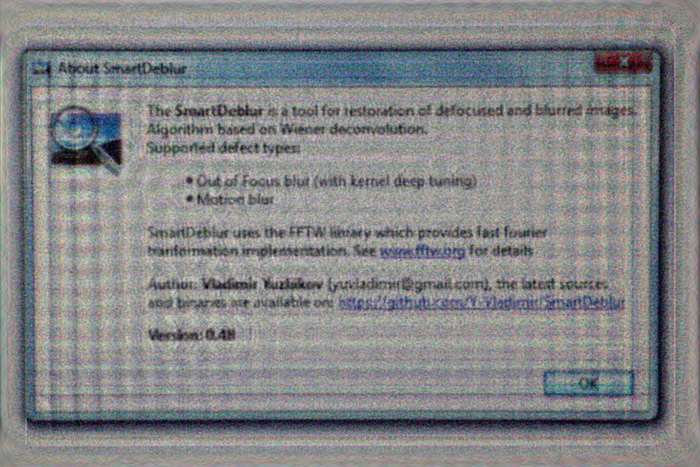
И вот результат обработки:
Практически весь текст читается достаточно хорошо, хотя и появились некоторые характерные искажения.
Под катом подробное описание проблем деконволюции, способов их решения, а также множество примеров и сравнений. Осторожно, много картинок!
Вспомним теорию
Подробное описание теории было в первой части, но все же напомню вкратце основные моменты. В процессе искажения из каждого пикселя исходного изображения получается некоторое пятно в случае расфокусировки и отрезок для случая обычного смаза. Все это друг на друга накладывается и в результате мы получаем искаженное изображение — это называется сверткой изображения или конволюцией. То, по какому закону размазывается один пиксель и называется функцией искажения. Другие синонимы – PSF (Point spread function, т.е. функция распределения точки), ядро искажающего оператора, kernel и другие.
Чтобы восстановить исходное изображение нам необходимо каким-то образом обратить свертку, при этом не забывая про шум. Но это не так-то просто – если действовать, что называется, «в лоб», то получится огромная система уравнений, которую решить за приемлемое время невозможно.
Но на помощь к нам приходит преобразование Фурье и теорема о свертке, которая гласит, что операция свертки в пространственной области эквивалентна обычному умножению в частотной области (причем умножение поэлементное, а не матричное). Соответственно, операция обратная свертке эквивалентна делению в частотной области. Поэтому процесс искажения можно переписать следующим образом:

где все элементы — это фурье-образы соответствующих функций:
G(u,v) – результат искажения, т.е. то, что мы наблюдаем в результате (смазанное или расфокусированное изображение)
H(u,v) – искажающая функция, PSF
F(u,v) – исходное неискаженное изображение
N(u,v) – аддитивный шум
Итак, нам нужно восстановить максимальное приближение к исходному изображению F(u,v). Просто поделить правую и левую часть на H(u,v) не получится, т.к. при наличии даже совсем небольшого шума (а он всегда есть на реальных изображениях) слагаемое N(u,v)/H(u,v), будет доминировать, что приведет к тому, что исходное изображение будет целиком скрыто под шумом.
Чтобы решить эту проблему, были разработаны более устойчивые методы, одним из которых являтся фильтр Винера (Wiener). Он рассматривает изображение и шум как случайные процессы и находит такую оценку f’ для неискаженного изображения f, чтобы среднеквадратическое отклонение этих величин было минимальным:

Функцией S здесь обозначаются энергетические спектры шума и исходного изображения соответственно – поскольку, эти величины редко бывают известны, то дробь Sn / Sf заменяют на некоторую константу K, которую можно приблизительно охарактеризовать как соотношение сигнал-шум.
Способы получения PSF
Итак, возьмем за отправную точки описанный фильтр Винера — вообще говоря, существует множество других подходов, но все они дают примерно одинаковые результаты. Так что все описанное ниже будет справедливо и для остальных методов деконволюции.
Основная задача — получить оценку функции распределения точки (PSF). Это можно сделать несколькими способами:
1. Моделирование. Очень непросто и трудоемко, т.к. современные объективы состоят из десятка, другого различных линз и оптических элементов, часть из которых имеет асферическую форму, каждый сорт стекла имеет свои уникальные характеристики преломления лучей с той или иной длиной волны. В итоге задача корректного расчета распространение света в такой сложнейшей оптической системе с учетом влияния диафрагмы, переотражений и т.п. становится практически невозможной. И решение ее, пожалуй, доступно только разработчикам современных объективов.
2. Непосредственное наблюдение. Вспомним, что PSF — это то, во что превращается каждая точка изображения. Т.е. если мы сформируем черный фон и одну белую точку на нем, а затем сфотографируем это с нужным значением расфокусировки, то мы получим непосредственно вид PSF. Кажется просто, но есть много нюансов и тонкостей.
3. Вычисление или косвенное наблюдение. Присмотримся к формуле (1) процесса искажение и подумаем, как можно получить H(u,v)? Решение приходит сразу — нужно иметь исходное F(u,v) и искаженное G(u,v) изображения. Тогда поделив фурье-образ искаженного изображения на фурье-образ исходного изображения мы получим искомую PSF.
Про боке
Перед тем как перейдем к деталям, расскажу немного теории расфокусировки применительно к оптике. Идеальный объектив имеет PSF в виде круга, соответственно каждая точка превращается в круг некоторого диаметра. Кстати, это для многих неожиданность, т.к. с первого взгляда кажется, что дефокус просто растушевывает все изображение. Это же объясняет и то, почему фотошоповское размытие Гаусса совсем не похоже на тот рисунок фона (его еще называют боке), который мы видим у объективов. На самом деле это два разных типа размытия — по Гауссу каждая точка превращается в нечеткое пятно (колокол Гаусса), а дефокус каждую точку превращает в круг. Соответственно и разные результаты.
Но идеальных объективов у нас нет и в реальности мы получаем то или иное отклонение от идеального круга. Именно это и формирует неповторимый рисунок боке каждого объектива, заставляя фотографов тратить кучу денег на объективы с красивым боке 🙂 Боке можно условно разделить на три типа:
— Нейтральное. Это максимальное приближение к кругу
— Мягкое. Когда края имеют меньшую яркость, чем центр
— Жесткое. Когда края имеют большую яркость, чем центр.
Рисунок ниже иллюстрирует это:
Более того, тип боке — мягкое или жесткое зависит еще и от того, передний это фокус или задний. Т.е. фотоаппарат сфокусирован перед объектом или же за ним. К примеру, если объектив имеет мягкий рисунок боке в переднем фокусе (когда, скажем, фокус на лице, а задний план размыт), то в заднем фокусе боке того же объектива будет жестким. И наоборот. Только нейтральное боке не меняется от вида фокуса.
Но и это еще не все — поскольку каждому объективу присущи те или иные геометрические искажения, то вид PSF зависит еще и от положения. В центре — близко к кругу, по краям — эллипсы и другие сплюснутые фигуры. Это хорошо видно на следующем фото — обратите внимание на правый нижний угол:
А теперь рассмотрим подробнее два последних метода получения PSF.
PSF — Непосредственное наблюдение
Как уже говорилось выше, необходимо сформировать черный фон и белую точку. Но просто напечатать на принтере одну точку недостаточно. Необходим намного большее отличие в яркости черного фона и белой точки, т.к. одна точка будет размываться по большому кругу — соответственно должна иметь большую яркость, чтобы быть видной после размытия.
Для этого я распечатал черный квадрат Малевича (да, тонера много ушло, но чего не сделаешь ради науки!), наложил с другой стороны фольгу, т.к. лист бумаги все же неплохо просвечивает и иголкой проколол маленькую дырочку. Затем соорудил нехитрую конструкцию из 200-ваттной лампы и сэндвича из черного листа и фольги. Выглядело это вот так:
Далее включил лампу, закрыл ее листом, выключил общий свет и сделал несколько фоток используя два объектива — китовый Canon EF 18-55 и портретник Canon EF 85mm/1.8. Из получившихся фоток я вырезал PSF и затем построил графики профилей.
Вот что получилось для китового объектива:
И для портретника Canon EF 85mm/1.8:
Хорошо видно как меняется характер боке с жествкого на мягкий для одного и того же объектива в случае переднего и заднего фокуса. Также видно, какую непростую форму имеет PSF — она весьма далека от идеального круга. Для портретника также видны большие хроматические аберрации из-за большой светосилы объектива и малой диафрагмы 1.8.
И вот еще пара снимков при диафрагме 14 — на нем видно, как поменялась форма с круга на правильный шестиугольник:
PSF — Вычисление или косвенное наблюдение
Следующий подход — косвенное наблюдение. Для этого, как писалось выше, нам нужно иметь исходное F(u,v) и искаженное G(u,v) изображения. Как их получить? Очень просто — необходимо поставить фотоаппарат на штатив и сделать один резкий и один размытый снимок одного и того изображения. Далее с помощью деления фурье-образа искаженного изображения на фурье-образ исходного изображения мы получим фурье-образ нашей искомой PSF. После чего применив обратное преобразование Фурье получим PSF в прямом виде.
Я сделал два снимка:
И в результате получил вот такую PSF:
На горизонтальную линию не обращайте внимания, это артефакт после преобразования Фурье в матлабе. Результат, скажем так, средненький — очень много шумов и детали PSF видны не так хорошо. Тем не менее, метод имеет право на существование.
Описанные методы можно и нужно использовать для построения PSF при восстановлении размытых изображений. Т.к. от того, насколько эта функция приближена к реальной напрямую зависит качество восстановления исходного изображения. При несовпадении предполагаемой и реальной PSF будут наблюдаться многочисленные артефакты в виде «звона», ореолов и снижения четкости. В большинстве случаев предполагается форма PSF в виде круга, тем не менее для достижения максимальной степени восстановления рекомендуется поиграться с формой этой функции, попробовав несколько вариантов от распространенных объективов — как мы видели, форма PSF может варьироваться в значительной степени в зависимости от диафрагмы, объектива и прочих условий.
Краевые эффекты
Следующая проблема заключается в том, что если напрямую применить фильтр Винера, то на краях изображения будет своеобразный «звон». Его причина, если объяснять на пальцах, заключается в следующем — когда делается деконволюция для тех точек, которые расположены на краях, то при сборке не хватает пикселей, которые находятся за краями изображения и они принимаются либо равным нулю, либо берутся с противоположной стороны (зависит от реализации фильтра Винера и преобразования Фурье). Выглядит это так:
Одно из решений, чтобы избежать этого состоит предобработке краев изображения. Они размываются с помощью той же самой PSF. На практике это реализуется следующем образом — берется входное изображение F(x,y), размывается с помощью PSF и получается F'(x,y), затем итоговое входное изображение F»(x,y) формируется суммированием F(x,y) и F'(x,y) с использованием весовой функции, которая на краях принимает значение 1 (точка целиком берется из размытого F'(x,y)), а на расстоянии равном (или большем) радиусу PSF от края изображения принимает значение 0. Результат получается такой — звон на краях исчез:
Практическая реализация
Я сделал программу, демонстрирующую восстановление смазанных и расфокусированных изображений. Написана она на C++ с использованием Qt. В качестве реализации преобразования Фурье я выбрал библиотеку FFTW, как самую быструю из опен-соурсных реализаций. Называется моя программа SmartDeblur, скачать ее можно на странице github.com/Y-Vladimir/SmartDeblur, все исходники открыты под лицензией GPL v3.
Скриншот главного окна:
Основные функции:
— Высокая скорость. Обработка изображения размером 2048*1500 пикселей занимает около 300мс в режиме Preview (когда перемещаются ползунки настроек) и 1.5 секунды в чистовом режиме (когда отпустили ползунки настроек).
— Подбор параметров в Real-time режиме. Нет необходимости нажимать кнопки Preview, все делается автоматически, нужно лишь двигать ползунки настроек искажения
— Вся обработка идет для изображения в полном разрешении. Т.е. нет никакого маленького окошка предпросмотра и кнопок Apply.
— Поддержка восстановления смазанных и расфокусированных изображений
— Возможность подстройки вида PSF
Основной упор при разработке был сделан на скорость. В итоге она получилась такая, что превосходит коммерческие аналоги в десятки раз. Вся обработка сделана по-взрослому, в отдельном потоке. За 300 мс программа успевает сгенерить новую PSF, сделать 3 преобразования Фурье, сделать деконволюцию по Винеру и отобразить результат — и все это для изображения размером 2048*1500 пикселей. В чистовом режиме делается 12 преобразований Фурье (3 для каждого канала, плюс одно для каждого канала для подавления краевых эффектов) — это занимает около 1.5 секунд. Все времена указаны для процессора Core i7.
Пока в программе есть ряд багов и особенностей — скажем, при некоторых значениях настроек изображение покрывается рябью. Точно причину выяснить не удалось, но предположительно — особенности работы библиотеки FFTW.
Ну и в целом в процессе разработки пришлось обходить множество скрытых проблем как в FFTW (например не поддерживаются изображения с нечетным размером одной из сторон, типа 423*440.). Были проблемы и с Qt — выяснилось, что рендеринг линии со включенным Antialiasing работает не совсем точно. При некоторых значениях углов линия перескакивала на доли пикселя, что давало артефакты в виде сильной ряби. Для обхода этой проблемы добавил строчки:
Сравнение
Осталось сравнить качество обработки с коммерческими аналогами.
Я выбрал 2 самые известные программы
1. Topaz InFocus — www.topazlabs.com/infocus
2. Focus Magic — www.focusmagic.com
Для чистоты эксперимента будем брать те рекламные изображения, которые приведены на официальных сайтах — так гарантируется, что параметры тех программ выбраны оптимальными (т.к. думаю, разработчики тщательно отбирали изображения и подбирали параметры перед публикацией в рекламе на сайте).
Итак, поехали — восстановление смаза:
Берем пример с сайта Topaz InFocus:
www.topazlabs.com/infocus/_images/licenseplate_compare.jpg
Обрабатываем с вот такими параметрами:

и получаем такой результат:
Результат с сайта Topaz InFocus:
Результат весьма схожий, это говорит о том, что в основе Topaz InFocus используется похожий алгоритм деконволюции плюс постобработка в виде заглаживания-удаления шумов и подчеркивания контуров.
Примеров сильно дефокусировки на сайте этой программы найти не удалось, да и она не предназначена для этого (максимальный радиус размытия составляет всего несколько пикселей).
Можно отметить еще один момент — угол наклона оказался ровно 45 градусов, а длина смаза 10 пикселей. Это наводит на мысль о том, что изображение смазано искусственно. В пользу этого факта говорит и то, что качество восстановления очень хорошее.