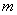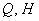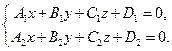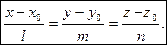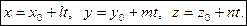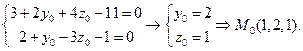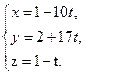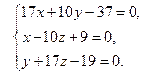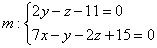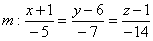Слово Как написать уравнение проекции прямой на плоскость - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Уравнение прямой в виде проекций на координатные плоскости

Параметрические уравнения прямой

Канонические уравнения прямой

Общие уравнения прямой

Прямая линия в общем виде определяется как линия пересечения двух плоскостей, то есть системой уравнений:

Любой ненулевой вектор , лежащий на данной прямой или параллельный ей, называется направляющим векторомпрямой.

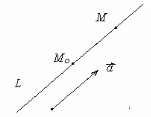
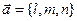
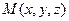
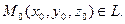
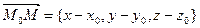
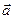
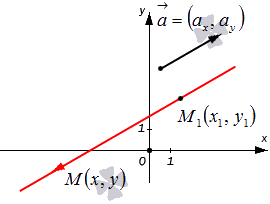
Пусть — текущая точка прямой, а Вектор коллинеарен вектору , следовательно, их координаты пропорциональны.

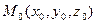
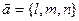
Каноническиеуравнения прямой, проходящей через точку и имеющей направляющий вектор , имеют вид:

Обозначим отношения, входящие в канонические уравнения прямой, через t:

.

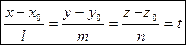
Отсюда получаем параметрические уравнения прямой в виде:

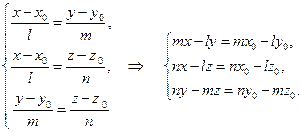
ПРИМЕР: Прямая задана общими уравнениями:(*)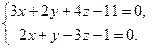

Составьте канонические и параметрические уравнения прямой. Напишите ее уравнение в виде проекций на координатные плоскости.

Найдем координаты точки, лежащей на прямой. Положим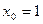, а две другие координаты найдем из системы (*):

В качестве направляющего вектора прямой выберем вектор, являющийся векторным произведением нормальных векторов плоскостей, линией пересечения которых будет искомая прямая.

,

Запишем канонические уравнения прямой: .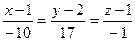
Параметрические уравнения прямой имеют вид:

Уравнение прямой в проекциях:

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Каноническое уравнение прямой на плоскости: теория, примеры, решение задач

Прямую линию в прямоугольной системе координат можно задать с помощью канонического уравнения. В этой статье мы расскажем, что это такое, приведем примеры, рассмотрим связи канонических уравнений с другими типами уравнений для этой прямой. В последнем пункте мы разберем несколько задач на закрепление темы.

Понятие канонического уравнения прямой

Таким образом, мы можем сформулировать необходимое и достаточное коллинеарности этих двух векторов:

Если преобразовать полученное равенство в координатную форму, то мы получим:

Из определения канонического уравнения нужно сделать несколько важных выводов. Вот они:

Разберем важный пример задачи на нахождение канонического уравнения.

Решение

Получившееся в итоге равенство и будет нужным ответом.

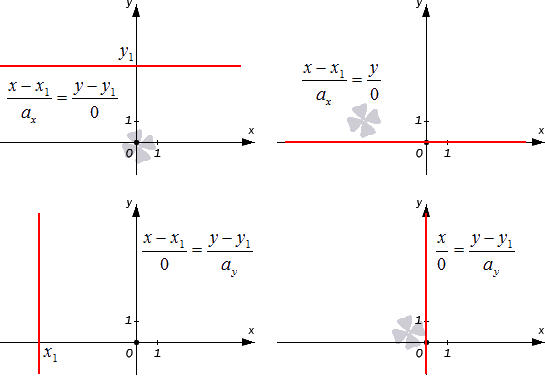
Проиллюстрируем два частных случая канонического уравнения, описанные выше:

Решение

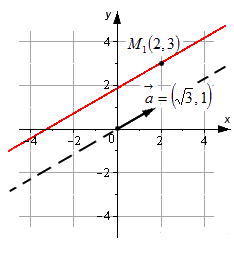
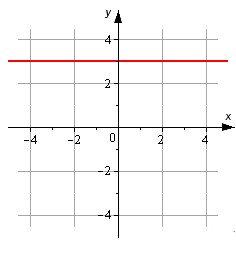
На рисунке изображена прямая. Запишите ее каноническое уравнение.

Решение

Преобразование канонического уравнения прямой в другие виды уравнений

Мы уже выяснили, что в прямоугольной системе координат на плоскости заданную прямую можно описать с помощью канонического уравнения. Оно удобно для решения многих задач, однако иногда лучше производить вычисления с помощью другого типа уравнений. Сейчас мы покажем, как преобразовать каноническое уравнение в другие виды, если это требуется по ходу решения.

Покажем на примере, как именно выполняется это действие с конкретными числами.

Решение

Далее можно перейти к формулированию необходимых параметрических уравнений:

Решение

Делаем указанные выше действия по порядку.

Также из канонического уравнения мы можем получить уравнение прямой в отрезках, прямой с угловым коэффициентом или нормальное уравнение прямой, но это действие выполняется в два шага: первым делом мы получаем общее уравнение прямой, а вторым – преобразуем его в уравнение указанного типа. Разберем пример такой задачи.

Решение

Для начала преобразуем исходное каноническое уравнение в общее уравнение прямой.

Далее переходим к формулировке уравнения прямой в отрезках.

У нас получилось нужное нам каноническое уравнение прямой на плоскости.

Решение

Таким же образом мы поступаем, если нам нужно привести к каноническому виду уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом.

Наиболее простая задача – переход от параметрических уравнений к каноническим. Нужно просто выразить параметр λ в системе уравнений x = x 1 + a x · λ y = y 1 + a y · λ и приравнять обе части равенств. Схема решения выглядит так:

Если значение одного из параметров a будет нулевым, мы поступаем точно таким же образом.

Решение

Как решать задачи на составление канонических уравнений

В первую очередь канонические уравнения используются для тех задач, где нужно выяснить, принадлежит ли некоторая точка заданной прямой или нет. Вспомним, что в случае, если точка лежит на прямой, ее координаты будут удовлетворять уравнению этой прямой.

Решение

Для проверки принадлежности необходимо подставить координаты точки в исходное уравнение и проверить, получим ли мы в итоге верное равенство.

Точно так же поступим и с координатами второй точки:

Получившееся в итоге равенство не является верным, значит, эта точка заданной прямой не принадлежит.

Ответ: первая точка лежит на заданной прямой, а вторая нет.

Решение

Равенство верное, значит, эта точка расположена на заданной прямой.

Далее мы посмотрим, какие еще типичные задачи на нахождение канонического уравнения можно встретить. Возьмем примеры с разными условиями.

Наиболее простыми являются задачи на нахождение канонического уравнения прямой на плоскости, в которых уже заданы координаты некой точки, лежащей на прямой. В первой части материала мы уже приводили пример решения такой задачи.

Чуть сложнее будет найти нужное уравнение, если нам предварительно нужно будет вычислить координаты направляющего вектора исходной прямой. Чаще всего встречаются задачи, в которой нужная прямая проходит через две точки с известными координатами.

Решение

Ответ: x 2 = y + 3 1

Посмотрим, как нужно составлять канонические уравнения прямой на плоскости в том случае, если направляющий вектор этой прямой нужно вычислять исходя из параллельных или перпендикулярных ей прямых.

Решение

Решение

Источник

Проекции прямой на координатные плоскости

Если прямая представляется уравнениями

,где С₁ и С₂ одновременно не равны нулю (случай когда С₁=С₂= 0 рассмотрен ниже в примере 2). Чтобы найти проекцию прямой на плоскость XOY, необходимо исключить z из уравнений (1) и (2). Полученное уравнение (вместе с уравнением z=0) будет представлять искомую проекцию. Аналогично находятся проекции на плоскости для YOZ и ZOX.

Пример 1
Найти проекцию прямой L

Решение
Для того, чтобы исключить z, умножим первое уравнение на 4, а второе — на 3 и затем сложим. Получим:

Это уравнение вместе с уравнением z=0 представляет проекцию L’ прямой L на плоскость XOY.

Пример 2
Найти проекции прямой L
2х-3у=0
х+у-4=0
на координатные плоскости.

Решение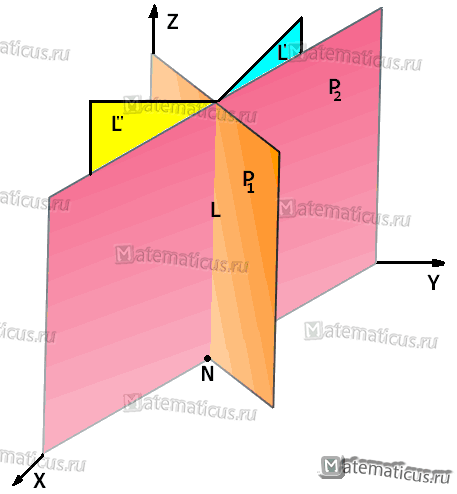

В данных уравнениях отсутствует z, потому что плоскости Р₁ и Р₂ перпендикулярны (Р₁⊥Р₂) к плоскости XOY. Прямая L перпендикулярна к XOY и проектируется на плоскость XOY в точку N с координатой z_N=0. Решая систему, находим значения x_N=12/5, у_N=8/5.
Уравнение проекции L’ на плоскость YOZ можно найти по общему способу, исключая х из уравнения. Получим у=8/5, то есть то же равенство, которое найдено выше для у_N. Уравнение проекции L» на плоскость XOZ будет x=12/5

Источник

Уравнения прямой, виды уравнений прямой в пространстве

Материал этой статьи продолжает тему прямой в пространстве. От геометрического описания пойдем к алгебраическому: зададим прямую при помощи уравнений в фиксированной прямоугольной системе координат трехмерного пространства. Приведем общую информацию, расскажем о видах уравнений прямой в пространстве и их связи между собой.

Уравнение прямой в пространстве: общие сведения

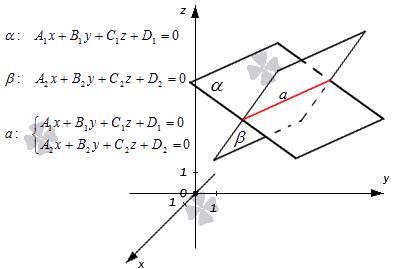
Уравнение прямой в пространстве как уравнение двух пересекающихся плоскостей

Когда две плоскости в пространстве имеют общую точку, существует их общая прямая, на которой находятся все общие точки этих плоскостей.

Рассмотрим это утверждение в алгебраическом толковании.

Таким образом, координаты любой точки прямой a в прямоугольной системе координат станут частным решением системы линейных уравнений вида

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0

Резюмируем: прямая в пространстве в прямоугольной системе координат O x y z может быть задана системой уравнений двух плоскостей, которые пересекаются:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0

Приведем пример описания прямой линии в пространстве при помощи системы уравнений:

Навык определения прямой линии уравнениями пересекающихся плоскостей необходим при решении задач на нахождение координат точки пересечения прямой и плоскости или нахождение координат точки пересечения двух прямых в пространстве.

Подробнее изучить эту тему можно, обратившись к статье об уравнениях прямой в пространстве, уравнениях двух пересекающихся прямых.

Заметим, что существует несколько способов описания прямой в пространстве. В практике прямую чаще задают не двумя пересекающимися плоскостями, а направляющим вектором прямой и точкой, принадлежащей этой прямой. В подобных случаях легче задать канонические и параметрические уравнения прямой в пространстве. Поговорим о них ниже.

Параметрические уравнения прямой в пространстве

x = x 1 + a x · 0 y = y 1 + a y · 0 z = z 1 + a z · 0 ⇔ x = x 1 y = y 1 z = z 1

Рассмотрим конкретный пример:

Продолжение изучения этой темы можно найти в статье о параметрических уравнениях прямой в пространстве.

Канонические уравнения прямой в пространстве

Если разрешить каждое из параметрических уравнений прямой

Графические иллюстрации подобных случаев, составление канонических уравнений прямой в пространстве, примеры решения типовых задач, а также алгоритм перехода от канонических уравнений к другим видам уравнений прямой в пространстве рассмотрены в статье о канонических уравнениях прямой в пространстве.

Источник

5.6.3. Как найти ортогональную проекцию прямой на плоскость?

г) Во-первых, что это за проекция?

Проведём очередную физкульт-пятиминутку:

Пожалуйста, найдите дома швабру и поместите её между ног. Представьте, что она бесконечна. Подбородок плотно прижат к груди. Теперь строго перпендикулярно смотрим вниз на швабру. при этом получается такое умное лицо…. Все выполнили задание? Тень от швабры – это и есть её ортогональная проекция на пол.

На чертеже выше наша «швабра» проведена малиновым цветом, а её проекция, прямая – коричневым цветом. Легко заметить, что проекция задаётся пересечением плоскостей: , и на самом деле ответ уже готов:

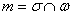
Другое дело, что часто требуется представить уравнения прямой в канонической форме, это стандартная задача:

Точка 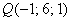, принадлежащая проекции, уже известна, осталось найти её направляющий вектор. Для быстроты используем формулу:

Таким образом, канонические уравнения проекции:

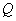
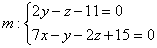
Как уже отмечалось, для решения этой задачи, не обязательно находить именно точку пересечения (лишняя работа). Нас устроит любая точка, принадлежащая проекции, и её легко подобрать из системы .

Есть и другой способ нахождения проекции, связанный с построением перпендикуляра к плоскости «сигма», но я тут прикинул, он вряд ли короче. Однако на всякий случай озвучу алгоритм, вдруг понадобится кому:

– находим точку пересечения прямой и плоскости: 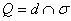(вот в этом способе уже обязательно находим);

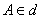
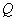
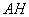
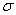
– берём произвольную точку , не совпадающую с точкой ) и опускаем из неё перпендикуляр на плоскость (см. следующие параграфы);

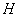
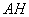
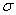
– находим основание перпендикуляра (как пересечение прямой и плоскости );

– составляем канонические уравнения проекции по двум точкам: .

Источник