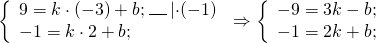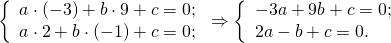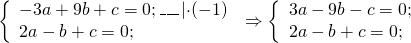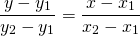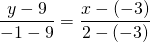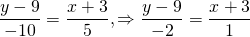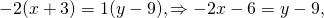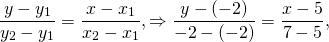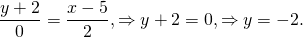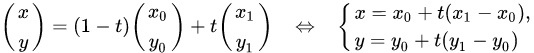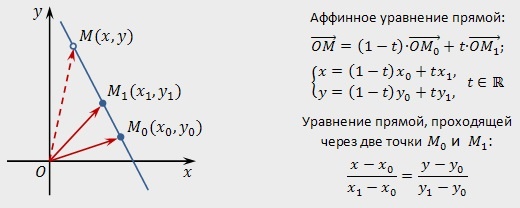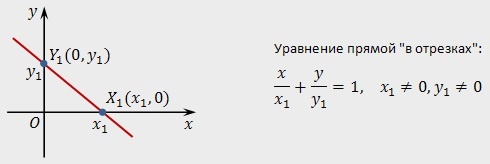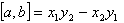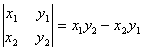Составить уравнение прямой, проходящей через две точки
Рассмотрим, как составить уравнение прямой, проходящей через две точки, на примерах.
Составить уравнение прямой, проходящей через точки A(-3; 9) и B(2;-1).
1 способ — составим уравнение прямой с угловым коэффициентом.
2 способ — составим общее уравнение прямой.
Общее уравнение прямой имеет вид ax+by+c=0. Подставив координаты точек A и B в уравнение, получаем систему:
Поскольку количество неизвестных больше количества уравнений, система не разрешима. Но можно все переменные выразить через одну. Например, через b.
получим: 5a-10b=0. Отсюда a=2b.
2bx+by-3b=0. Осталось разделить обе части на b:
Общее уравнение прямой легко приводится к уравнению прямой с угловым коэффициентом:
3 способ — составим уравнение прямой, проходящей через 2 точки.
Уравнение прямой, проходящей через две точки, имеет вид:
Подставим в это уравнение координаты точек A(-3; 9) и B(2;-1)
В школьном курсе чаще всего используется уравнение прямой с угловым коэффициентом. Но самый простой способ — вывести и использовать формулу уравнения прямой, проходящей через две точки.
Если при подстановке координат заданных точек один из знаменателей уравнения
окажется равным нулю, то искомое уравнение получается приравниваем к нулю соответствующего числителя.
Подставляем в уравнение прямой, проходящей через 2 точки, координаты точек C и D:
Составить уравнение прямой, проходящей через точки M (7; 3) и N (7; 11).
Уравнение прямой, проходящей через две точки онлайн
С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через две точки. Дается подробное решение с пояснениями. Для построения уравнения прямой задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точек в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Уравнение прямой, проходящей через две точки − примеры и решения
Подставив координаты точек A и B в уравнение (1), получим:
 |
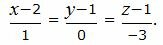 |
(Здесь 0 в знаменателе не означает деление на 0).
Составим параметрическое уравнение прямой:
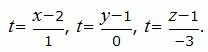 |
Выразим переменные x, y, z через параметр t :
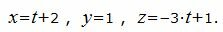 |
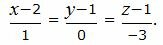 |
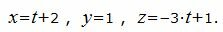 |
Пример 2. Построить прямую, проходящую через точки A(1, 1/5, 1) и B(−2, 1/2, −2).
Подставив координаты точек A и B в уравнение (2), получим:
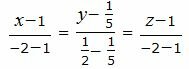 |
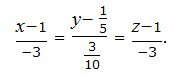 |
Составим параметрическое уравнение прямой:
 |
Выразим переменные x, y, z через параметр t :
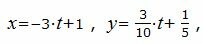 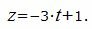 |
Каноническое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:
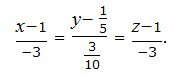 |
Параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:
Уравнение прямой
Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
Уравнение прямой в отрезках на осях
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x 0 y = m t + y 0
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a =
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
 | x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n =
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
Уравнение прямой, проходящей через 2 точки
Суть уравнения прямой, проходящей через две заданные точки
Необходимо сделать вывод формулы для прямой, которая пересекает эти заданные точки.
Точка \(М (х, у)\) соответствует прямой \(M_ <0>M_<1>\) только в том случае, когда ее радиус-вектор \(\vec
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Где t является некоторым действительным числом (параметром). Координатная форма уравнения имеет следующий вид:
Определив параметр t с помощью первого и второго уравнений системы, можно получить доказательство следующего соотношения:
Формула будет иметь следующий вид:
Данное равенство вытекает из канонического уравнения, если выбрать направляющим вектором:
Вектор \(\vec
То есть, замещая следующие параметры:
Уравнение прямой в отрезках
Пусть координатные оси включают две точки: \(X_<1>\left(x_<1>,0 \right)\) и \(Y_<1>\left(0, y_ <1>\right)\)
Следует отметить следующее условие:
Необходимо записать уравнение прямой, которая проходит через заданные точки, подставив в формулу:
В результате уравнение принимает следующий вид:
Если поменять местами правую и левую части уравнения, то равенство примет такой вид:
Данную формулу называют уравнением прямой в отрезках. С помощью прямой, которая пересекает точки: \(X_<1>\left(x_<1>,0 \right)\) и \(Y_<1>\left(0, y_ <1>\right)\)
координатные оси делят на отрезки х1 на оси абсцисс и у1 на оси ординат. Длины отрезков будут рассчитаны следующим образом:
Как записать формулу, канонический вид
Какой-либо вектор, отличный от нуля, проходит по данной прямой или параллельно ей, называют направляющим вектором этой прямой. Для обозначения направляющего вектора произвольной прямой используют букву \(\bar\)
Координаты данного вектора обозначают с помощью букв l, m, n. Таким образом, можно прийти к следующему уравнению:
Уравнение в таком виде называют каноническим.
Параметрическое уравнение прямой, проходящей через две точки
Канонические уравнения для прямой, которая пересекает следующие точки:
будет записано в следующем виде:
Равные отношения можно обозначить буквой t в канонических уравнениях. В итоге они приобретают такой вид:
Исход из этого, получается равенство:
Данные равенства являются параметрическими уравнениями прямой, которая пересекает точку \(M_<0>\left(x_<0>;y_<0>; z \right)\) в направлении вектора \(\bar=\left\
В данном случае t является произвольно изменяющимся параметром, x, y, z представляют собой функции от t. Если изменяется t, то значения x, y, z также меняются. Таким образом, точка M (x; y; z) перемещается вдоль прямой. Если параметр t использовать в качестве переменного времени, а уравнения представить в виде формул, описывающих движение точки М, то с помощью данных уравнений можно определить прямолинейное и равномерное движение точки М. При t равным 0 точка М будет совпадать с точкой M0.
Скорость V точки М обладает постоянным значением и рассчитывается по формуле:
Примеры задач с решением
Задача 1
Решение
Уравнение прямой, которая проходит через точки:
будет иметь следующий вид:
После того, как координаты точек А и В будут применены к первому уравнению, оно будет записано в такой форме:
После некоторых преобразований получается:
В данном случае наличие ноля в знаменателе не обозначает деление на ноль. Параметрическое уравнение прямой будет записано таким образом:
Если выразить переменные x, y, z с помощью параметра t, в итоге получится:
Задача 2
Решение
Уравнение для прямой, которая пересекает заданные точки:
будет записано таким образом:
После подстановки координат точек А и В в исходную формулу, она приобретет такой вид:
Далее можно записать параметрическое уравнение прямой:
Выразив переменные x, y, z с помощью параметра t, можно получить следующее уравнение:
Ответ: каноническое уравнение прямой, пересекающей заданные точки A(1, 1/5, 1) и B(−2, 1/2, −2) записано в следующем виде:
параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:
Урок 29. Нахождение уравнение прямой по двум точкам
Урок из серии «Геометрические алгоритмы»
Здравствуйте, дорогой читатель!
Сегодня мы начнем изучать алгоритмы, связанные с геометрией. Дело в том, что олимпиадных задач по информатике, связанных с вычислительной геометрией, достаточно много и решение таких задач часто вызывают затруднения.
За несколько уроков мы рассмотрим ряд элементарных подзадач, на которые опирается решение большинства задач вычислительной геометрии.
На этом уроке мы составим программу для нахождения уравнения прямой, проходящей через заданные две точки. Для решения геометрических задач нам понадобятся некоторые знания из вычислительной геометрии. Часть урока мы посвятим знакомству с ними.
Сведения из вычислительной геометрии
Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач.
Исходными данными для таких задач могут быть множество точек на плоскости, набор отрезков, многоугольник (заданный например, списком своих вершин в порядке движения по часовой стрелке) и т.п.
Результатом может быть либо ответ на какой то вопрос (типа принадлежит ли точка отрезку, пересекаются ли два отрезка, …), либо какой-то геометрический объект (например, наименьший выпуклый многоугольник, соединяющий заданные точки, площадь многоугольника, и т.п.).
Мы будем рассматривать задачи вычислительной геометрии только на плоскости и только в декартовой системе координат.
Векторы и координаты
Чтобы применять методы вычислительной геометрии, необходимо геометрические образы перевести на язык чисел. Будем считать, что на плоскости задана декартова система координат, в которой направление поворота против часовой стрелки называется положительным.
Теперь геометрические объекты получают аналитическое выражение. Так, чтобы задать точку, достаточно указать её координаты: пару чисел (x; y). Отрезок можно задать, указав координаты его концов, прямую можно задать, указав координаты пары ее точек.
Но основным инструментом при решении задач у нас будут векторы. Напомню поэтому некоторые сведения о них.
Отрезок АВ, у которого точку А считают началом (точкой приложения), а точку В – концом, называют вектором АВ и обозначают либо 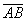
Для обозначения длины вектора (то есть длины соответствующего отрезка) будем пользоваться символом модуля (например, 
Произвольный вектор 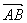
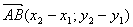
здесь точки A и B имеют координаты 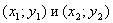
Для вычислений мы будем использовать понятие ориентированного угла, то есть угла, учитывающего взаимное расположение векторов.
Ориентированный угол между векторами a и b положительный, если поворот от вектора a к вектору b совершается в положительном направлении (против часовой стрелки) и отрицательный – в другом случае. См рис.1а, рис.1б. Говорят также, что пара векторов a и b положительно (отрицательно) ориентирована.
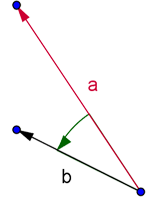 Рис. 1а | 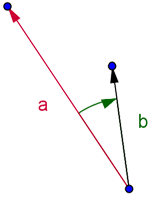 Рис. 1б |
Таким образом, величина ориентированного угла зависит от порядка перечисления векторов и может принимать значения в интервале 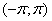
Многие задачи вычислительной геометрии используют понятие векторного (косого или псевдоскалярного) произведений векторов.
Векторным произведением векторов a и b будем называть произведение длин этих векторов на синус угла между ними:
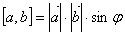
Векторное произведение векторов в координатах:
Выражение справа — определитель второго порядка:
В отличии от определения, которое дается в аналитической геометрии, это скаляр.
Знак векторного произведения определяет положение векторов друг относительно друга:
Если величина 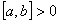
Если величина 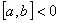
Векторное произведение ненулевых векторов равно нулю тогда и только тогда, когда они коллинеарны ( 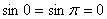
Рассмотрим несколько простейших задач, необходимых при решении более сложных.
Уравнение прямой
Определим уравнение прямой по координатам двух точек.
Уравнение прямой, проходящей через две различные точки, заданные своими координатами.
Пусть на прямой заданы две не совпадающие точки: 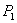
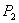
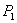
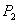
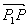
С помощью векторного произведения условие коллинеарности векторов 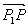
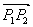
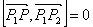
(y2-y1)x + (x1-x2)y + x1(y1-y2) + y1(x2-x1) = 0
Последнее уравнение перепишем следующим образом:
Итак, прямую можно задать уравнением вида (1).
Задача 1. Заданы координаты двух точек. Найти её представление в виде ax + by + c = 0.
На этом уроке мы познакомились с некоторыми сведениями из вычислительной геометрии. Решили задачу по нахождению уравнения линии по координатам двух точек.
На следующем уроке составим программу для нахождения точки пересечения двух линий, заданных своими уравнениями.