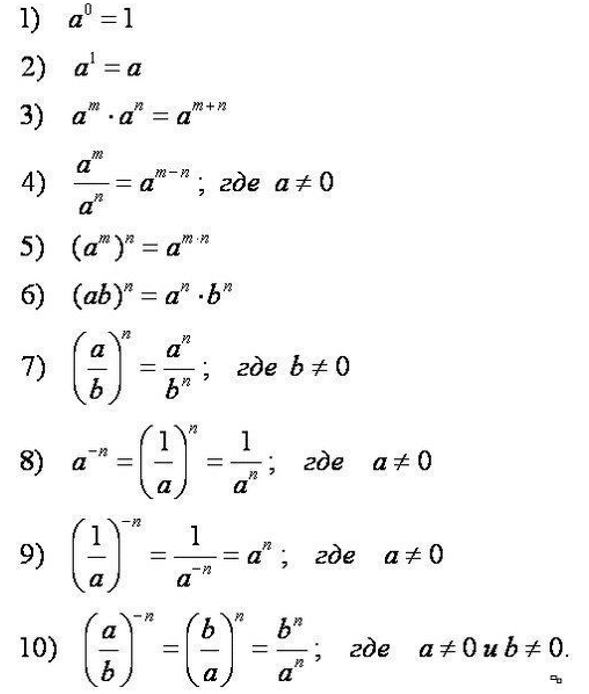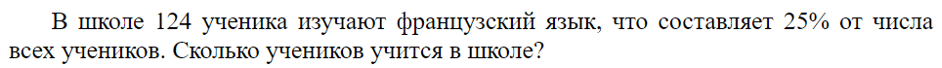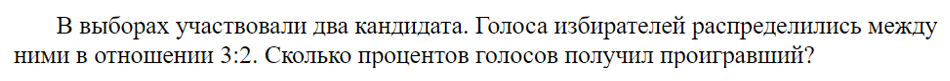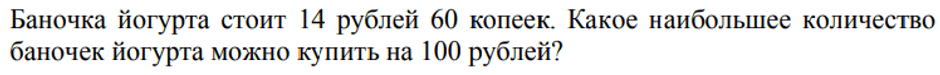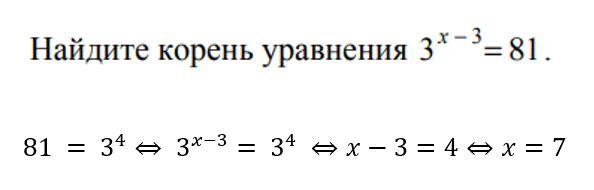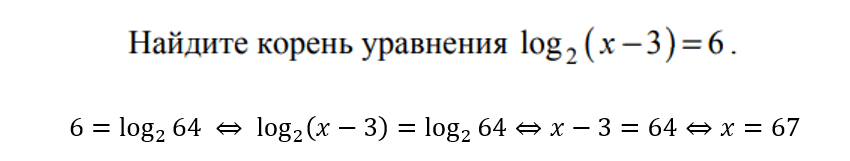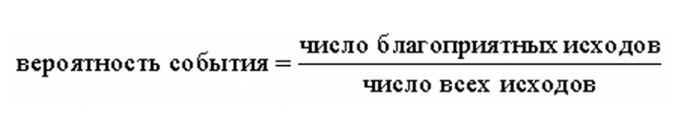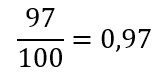Как сдать экзамен, если ничего не знаешь? Хитрости, советы
Главное правило зачётной книжки никто не отменял
«Сначала студент работает на зачётку, потом зачётка работает на студента». Первокурсникам тяжело поверить в то, что зачётка будет работать на них в последние несколько лет обучения, но эта истина подтверждена не один раз. Почти все преподаватели обращают внимание на успеваемость по другим дисциплинам и на прошлых курсах, эта информация прямо влияет на результат экзамена. Это же касается и текущих оценок по предмету. Если журнал украшают двойки и прогулы, то получить хороший балл на экзамене будет непросто.
Экзамен «автоматом»
Такой способ сдачи экзаменов придется по душе ответственным и старательным студентам. Все знают: чтобы получить «автомат», нужно регулярно посещать лекции и практические занятия, участвовать в олимпиадах и конференциях по предмету, быть активным на уроках и иметь хорошие текущие оценки. Такого студента преподаватель обязательно заметит на протяжении семестра и выставит оценки в зачётку без дополнительной проверки знаний.
Но, как ни крути, этот способ сдачи экзаменов сложный и требует массы усилий. Нас же, наоборот, интересует, как сдать экзамен, если ничего не знаешь и не хочешь учить.
Шпаргалки обязательны!
Также важно вовремя себя спросить: сдам ли я экзамен? Если до «судного» дня остаётся ещё немного времени, то нужно срочно приступать к написанию шпаргалок. Сможете ли вы воспользоваться ими – это уже совсем другой вопрос, но приготовить их обязательно нужно.
Важно не просто скачать с Интернета готовые шпоры, распечатать их и вырезать, а сделать их самостоятельно. Написание записок с подсказками подразумевает чтение, выбор материала и непроизвольное запоминание информации, с которой вы работаете. После этого во время экзамена вам проще будет ориентироваться в тех шпаргалках, которые вы сами составили. Если преподаватель настолько строго контролирует обстановку в аудитории, что списать становится нереально, — поможет память. Гораздо легче вспомнить то, что вы совсем недавно самостоятельно писали на шпаргалку.
Помните, что списывать – это рискованное занятие, и важно знать, сколько раз можно сдавать экзамен конкретно у этого преподавателя. Подумайте, позволят ли вам прийти на пересдачу, если обман будет раскрыт.
Используем современные достижения науки и техники
В советском фильме показывали, как для успешной сдачи экзаменов студенты использовали наушники и радиопередатчик. Современным ученикам в этом плане намного проще. Мобильные телефоны, смартфоны, планшеты, диктофоны намного компактней советской радиоаппаратуры, а связь с Интернетом даёт неограниченный доступ к любой информации. Многие выбирают такой способ, чтобы, ничего не зная по предмету, сдать экзамен. ЕГЭ, скорей всего, не получится осилить, используя гаджеты, ведь там очень строгие проверки наличия телефонов и прочих технических приспособлений, но они вполне могут спасти ситуацию на экзаменах в вузах.
Спасёт хорошая репутация
Как хорошо сдать экзамен, не прилагая особых усилий к изучению предмета, а пользуясь только харизмой и хорошим авторитетом? Задуматься о том, что вам предстоит сдавать экзамен, нужно заранее и с первого знакомства с преподавателем начинать создавать о себе хорошее впечатление.
Это может быть участие в самодеятельности, помощь в организации субботников, написание статей в студенческую газету. Также нужно создавать впечатление любознательного ученика. Почаще задавайте на лекциях вопросы и делитесь информацией, которую вы услышали из телепрограмм и прочитали в журналах, если она касается темы урока. Можно также интересоваться научными трудами преподавателя и его диссертациями.
Как вести себя на экзамене
Итак, наступает день сдачи. Как сдать экзамен, если ничего не знаешь? Важно следовать правилам поведения, которые помогут получить хорошие баллы за сомнительные знания:
Крайние меры
Если, несмотря на все старания сдать экзамен, ничего не зная, вы понимаете, что единственная оценка, которая вам светит, – это неуд, нужно идти на крайние меры.
Можно предложить преподавателю решить вопрос полюбовно. Некоторые из них согласны повысить балл, если вы сможете быть ему чем-то полезным. Например, сделаете уборку в аудитории, или купите новый набор колб для опытов по химии. Иные преподаватели способны поменять гнев на милость, если вы заявитесь к ним с бутылочкой хорошего коньяка. В этом деле важно быть очень осторожным, и попытаться найти персональный подход к каждому. Помните, что в случае отказа преподавателя от такого варианта решения вопроса, сдать экзамен на свои знания вам будет сложнее. Возможно, вас ждут завышенные требования к качеству ответов и дополнительные каверзные вопросы.
Полезные советы для тех, кто хочет хорошо сдать экзамен
Вы узнали, как сдать экзамен, если ничего не знаешь, и увидели, что, применяя определенную стратегию, получить высокий балл, обладая низкими знаниями, не составит особого труда. Но следует помнить, что отсутствие знаний за пределами учебных аудиторий может обернуться более серьёзной проблемой, чем «кол» на экзамене.
Как сдать экзамен по математике
Соавтор(ы): Grace Imson, MA. Грейс Имсон — преподаватель математики с более чем 40 годами опыта. В настоящее время преподает математику в Городском колледже Сан-Франциско, ранее работала на кафедре математики в Сент-Луисском университете. Преподавала математику на уровне начальной, средней и старшей школы, а также колледжа. Имеет магистерскую степень по педагогике со специализацией на руководстве и контроле, полученную в Сент-Луисском университете.
Количество источников, использованных в этой статье: 9. Вы найдете их список внизу страницы.
Количество просмотров этой статьи: 80 548.
Предстоящий экзамен по математике может пугать, особенно если вы не очень сильны в этом предмете. Тем не менее, предварительная подготовка и выбор правильной стратегии помогут вам успешно сдать экзамен. Лучше всего начать готовиться к экзамену заранее, хотя бы за несколько дней или даже недель. Тем не менее, можно кое-что предпринять и в том случае, если для подготовки у вас остался лишь один день. Если же у вас совсем не осталось времени, сосредоточьтесь на том, что вы уже знаете, и используйте некоторые приемы, чтобы получить как можно более высокую оценку.
Убедитесь, что вы твердо усвоили основы математики. Чтобы успешно сдать любой экзамен по математике, необходимо владеть ее основами, особенно умножением. Даже если экзамен посвящен сокращению дробей, вам понадобится твердое знание таблицы умножения.
Совет: если вам нравится учиться совместно с другими людьми, попробуйте организовать группу по изучению математики или присоединиться к такой группе, если она уже есть.
Личный опыт: как сдать математику на 100 баллов
Поговорили с выпускницей «Фоксфорда» о том, как готовиться к профильной математике и сдать на сотку
Профильную математику ЕГЭ часто называют одним из самых сложных экзаменов. Однако некоторым школьникам удаётся сдать его идеально, на 100 баллов. В новом материале рассказываем историю Аси, которой удалось это сделать и поступить в вуз мечты.
Почему ты решила сдавать профильную математику на ЕГЭ?
В 10-м классе я начала задумываться о поступлении в экономический вуз, куда требовалась профильная математика. До этого я не планировала связывать свою жизнь ни с математикой, ни с экономикой, но потом поняла, что мне это интересно.
Как ты начала готовиться?
В 10-м классе я смотрела видео Бориса Трушина на ютьюбе, а потом сама решала и разбирала задачи из второй части. Моя подготовка была довольно хаотичной, систематически я стала заниматься только в выпускном классе.
Записалась на годовой курс к Борису Трушину и готовилась ко второй части. Первую часть мы решали в школе, поэтому дополнительно я с ней не сидела. Примерно раз в две недели я прорешивала вторую часть целиком. Варианты брала из сборников «Решу ЕГЭ», тематических книг и пабликов — там они обычно сложнее, чем на экзамене.
Какая была самая сложная тема для тебя?
Больше всего трудностей у меня возникало при работе с теорией чисел. Задание 19 «в» я решала с переменным успехом, потому что на этой позиции встречаются очень разные задачи. Ещё было сложновато со стереометрией, так как там нужно пространственное мышление, но я более-менее разобралась.
Даже во время самого экзамена больше всего сложностей у меня вызвало задание 14. Оно было посвящено стереометрии. Пункт «б» меня тоже поставил в ступор — получились большие числа под корнями, поэтому, вероятно, проблема была в арифметике.
А какая — самая простая?
Я не могу вспомнить какую-то одну тему, которая казалась бы мне самой лёгкой. Возможно, быстрее всего мне давалось решение уравнений. Они есть и в первой, и во второй части, и решала я их очень быстро.
Что ты чувствовала во время сдачи ЕГЭ?
Я очень нервничала на экзамене, и несколько раз меня просто охватывала полная паника. Я не сразу поняла параметр в одном из заданий, у меня поначалу не получались задания 14 и 16. Задание 19 я сделала тоже не с первой попытки.
На экзамен я потратила все четыре часа и вышла из кабинета последней.
Я была расстроена после ЕГЭ, мне казалось, у меня будет баллов 80.
Какая была твоя первая реакция на заветные 100 баллов?
За пару дней до объявления результатов я посмотрела решение своего варианта в интернете. Поэтому я уже знала, что в основном решила всё верно, но не думала, что на 100. Когда я увидела результаты, закричала на всю квартиру. Родители начали меня обнимать, мы все были в шоке. Я где-то сутки пыталась осознать происходящее.
Как думаешь, в чём твой секрет успеха?
Думаю, большую роль сыграла моя любовь к математике. Я могла спокойно просидеть полдня с задачами по математике, меня это не напрягало в отличие от, например, обществознания и английского. К тому же у меня была требовательная учительница по математике в школе, поэтому к 10-му классу у меня была очень хорошая база знаний, мне не нужно было поднимать предмет с нуля.
Перед экзаменом я настраивала себя на то, что получу 100 баллов. В меня верили мои родители, друзья, они поддерживали меня, да и Борис Трушин всегда говорил, что сдать на 100 баллов реально.
Помимо подготовки к самим заданиям важно не забывать о психологической подготовке: если человек не верит в то, что он может сдать на 100, он не сможет сдать на 100.
Куда ты в итоге поступила?
Я поступила в НИУ ВШЭ в Петербурге на экономику. Слышала много хорошего об этом вузе, поэтому давно хотела именно туда. Для поступления мне нужна была профильная математика. Более того, на первом курсе у нас много математики, поэтому навыки решения экзаменационных задач мне пригодились.
Можешь дать какой-то совет тем, кто планирует сдавать ЕГЭ по профильной математике?
Не бойтесь математики. Многие говорят, что это сложный и страшный экзамен: варианты в книжках и на сайтах сложнее самого экзамена, поэтому учителя и репетиторы просто запугивают этими вариантами. На самом деле, если готовиться к экзамену и решать задания именно с реальных ЕГЭ, можно написать его на очень высокий балл.
Важно при этом не зазубривать формулы и не заучивать алгоритмы решений, а именно понимать, что происходит в задаче и как её можно решить.
Если у вас слабая база, то начинать готовиться нужно в 10-м классе, а с хорошей базой можно, наверно, и в 11-м начать, но в начале года, а не весной.
Изображение на обложке: Monograph / Dribbble
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter
Быстро подготовиться к базовой математике — инструкция к каждому заданию
Антонина Белова
Обычно базовую математику выбирают ребята, у которых есть план: надо как можно скорее разделаться с бесполезным для поступления предметом и сосредоточиться на своем наборе вступительных. Из этой статьи вы узнаете, как сдать базовую математику максимально быстро и просто.
В этом материале мы сделаем акцент на простых номерах, которые принесут вам балл почти задаром! Их выделили пометкой «Делаем обязательно», и таких заданий 10 штук. Как раз с запасом на ошибки.
Для тех, кто хочет получить выше тройки, мы дали рекомендации по еще 4 задачкам. Итого мы рассмотрели 14 номеров. Стоит сделать их все, и твердая четверка у вас в кармане.
Научим решать сложные задания
ЕГЭ по математике
на пробном уроке в MAXIMUM
Задание 1 (Делаем обязательно!)
Задание проверяет базовые навыки счета, которым вы научились в 5-6 классах. Для получения балла надо:
Уделите пару вечеров отработке алгоритмов сложения, вычитания, умножения и деления простых и десятичных дробей. Мы лично знаем ребят, которые не могут правильно разделить десятичные дроби в 11 классе!
Задание 2 (Делаем обязательно!)
Задача чуть сложнее: пример со степенями. Для выполнения надо:
Нужная теория будет в справочных материалах на экзамене, но это не поможет, если не наработан навык ею пользоваться. Практика обязательна.
Задание 3
Составители экзамена проверяют ваш навык работы с процентами. Задачи на проценты бывают трех типов:
Тип 1. Найти часть от числа
Часть может быть выражена в процентах или сразу в виде дроби. Например, придется искать треть от чего-то.
Рассмотрим на примере реальной задачи из экзамена:
Прочувствуйте специфику задачи: нам известно целое — вся зарплата до вычета налога. А работать мы будем с кусочком — 13-ю процентами. Сколько это в рублях нам еще предстоит узнать.
Чтобы ответить на вопрос задачи, делаем 3 шага:
А. Переводим процент в десятичную дробь
Для этого всегда надо количество процентов поделить на 100.
Б. Находим, сколько это от зарплаты в рублях
Запоминаем главное правило для этого типа задач: чтобы найти дробь от числа, надо число на эту дробь умножить.
12 500 * 0,13 = 1 625 (р.) — налог, который удержат с зарплаты Ивана Кузьмича.
В. Отвечаем на вопрос задачи
У нас просили зарплату после вычета налога, а не сам налог.
12 500 — 1625 = 10 875 (р.)
Будьте внимательны, многие завалятся именно на последнем шаге!
Тип 2. Найти число по его части
Прочувствуйте разницу с прошлой задачей: тут 124 это и есть 25%, то есть одна и та же величина выражена в процентах и в абсолютных величинах, в данном случае — в учениках. Просят узнать целое — 100%.
А. Переводим процент в десятичную дробь
Б. Находим, сколько учеников всего
Правило для этого типа задач: чтобы найти целое, надо часть разделить на дробь.
124 : 0,25 = 496 (у.) — всего.
Тип 3. Найти, сколько процентов часть составляет от целого
Особенность подобных заданий — не дано процентов, есть только абсолютные величины. В данном случае — стоимость футболки в рублях.
А. Находим, какую долю новая цена составляет от первоначальной
Запоминаем правило: чтобы найти, какую долю часть составляет от целого, надо часть на целое разделить.
Б. Переводим долю в процент
В прошлых задачах мы уже дважды выполнили обратное действие. В этот раз сделаем наоборот: умножим полученную дробь на 100
0,85 * 100 = 85 % — столько процентов новая цена составляет от старой
В. Отвечаем на вопрос задачи
Нас спросили, на сколько процентов цена снизилась, что стала 85% от первоначальной? Конечно, изначально она была 100%. Итого
Остался последний тип, не так явно связанный с процентами…
Тип 4. Задачи на соотношение
Если чуть перефразировать условие, то за первого кандидата проголосовали 3 части избирателей, а за второго — 2 части. Особенность этих частей в том, что они ОДИНАКОВЫЕ по величине.
Если одна будет состоять из 10 человек, то за первого кандидата будет 30, а за второго — 20.
А. Считаем общее количество частей
Б. Узнаем, сколько голосов составляет одна такая часть
Тут речь о процентах проголосовавших. Сколько всего проголосовало? Конечно, 100%! Значит каждая из пяти частей «весит»…
В. Отвечаем на вопрос задачи
За проигравшего проголосовало меньше частей избирателей. В нашем случае 2.
Решение этих задач удобнее всего оформить табличкой
| 1 кандидат | 2 кандидат | Всего | |
| Части | 3 | 2 | 5 |
| Абсолютные величины | 20% * 2= 40% | 100 % |
1 часть = 100% : 5 = 20%
Если рассчитываете решать текстовую задачу, включите здравый смысл! Ответ всегда можно проверить на адекватность благодаря обычной логике. Без нее и выстроить ход решения выйдет вряд ли.
Задание 4 (Делаем обязательно!)
Задание проверяет навык работы с формулами. Алгоритм решения напоминает решение задачек на уроке по физике:
Самое трудное тут — правильно выразить искомую величину: повторяем порядок выполнения арифметических операций, свойства умножения, тренируемся перекидывать через равно множители и слагаемые.
И да, в базе часто эта задача проста настолько, что даже перекидывать ничего не придется, нужная величина уже будет слева от равно.
Задание 5
Задачка чуть сложнее: придется поработать с выражением. Чтобы точно получить балл, надо подготовиться ко всем возможным вариантам номера. Чтобы сдать базовую математику, нужно повторить и, самое главное, научиться применять:
Да, почти вся эта теория будет у вас на экзамене в справочных материалах, но еще раз: не надейтесь грамотно ею воспользоваться без наработанного навыка.
Задание 6 (Делаем обязательно!)
Проверяется ваше умение разделить случаи, когда требуется округлить величину в большую сторону, а когда — в меньшую.
Если ходите в магазин с карманными деньгами, то сталкиваетесь с подобными задачами каждый день! Разделим 100 рублей на стоимость одной упаковки йогурта. Не забываем приводить все величины к одной размерности:
Так сколько баночек йогурта вам продадут? На 7 штук вам явно не хватает денег, значит округлить полученную величину надо до целого в меньшую сторону. Математическое правило округление в этой задаче не поможет.
Одна пачка на 6 рулонов, значит на 63 рулона:
Но опять же, никто полпачки вам не продаст. Включаем логику: возьмем меньше — не хватит еще половины пачки на 3 последние рулона. Значит округлить надо в большую сторону, взять клей с небольшим запасом. Снова математическое правило округления игнорируем.
Задание 7 (Делаем обязательно!)
Хотите сдать базовую математику — вам повезло! В номере с уравнениями не попадется тригонометрического. Зато могут быть..
Раскрываем скобки, если они есть, слагаемые с «х» переносим в одну сторону от равно, без «х» — в другую. Приводим подобные и решаем простейшее уравнение.
Бывают полные и неполные, всего надо повторить 3 алгоритма решения! А формула дискриминанта еще и в справочных материалах есть.
Это те, что с корнем. Чтобы избавиться от корня, возводим обе части уравнения в квадрат и решаем получившееся уравнение. Есть нюансы с областью допустимых значений (ОДЗ): подставьте полученные корни в исходное уравнение и проверьте, выполняется ли равенство. Если нет, то подставленное значение решением не будет.
Чуть веселее. Ваша задача — с помощью формул свойств степеней привести уравнение к виду, когда слева и справа от равно в основании степени будет одно и то же число. После приравниваем показатели и решаем. Вот так:
Еще чуть веселее. С помощью формул свойств логарифмов приводим уравнение к виду, когда слева и справа от равно будет логарифм с одинаковым основанием. После приравниваем выражения под логарифмом и решаем.
Тут тоже могут быть особенности с ОДЗ. Проверяйте подстановкой.
Прелесть уравнений в том, что ответ всегда можно проверить подстановкой вместо икса в уравнение! Не забывайте проверять, ведь это возможность убедиться на 100%, что заветный балл не проплывет мимо. Только так можно уверенно сдать базовую математику.
Задание 9 (Делаем обязательно!)
Задача на здравый смысл. Нужно соотнести величины с их возможными значениями.
Вряд ли грузовой автомобиль может весить как 3 шоколадки (300 г), а взрослый человек 8 тонн.
Главное — внимательно перенести ответы в бланк.
Задание 10 (Делаем обязательно!)
Простая задача на определение вероятности.
Решаем с помощью формулы:
Внимательно читаем вопрос: спрашивают вероятность купить исправную лампочку. Если из ста 3 неисправны, значит остальные в порядке, и нам подойдет любая из оставшихся 97 штук. Это и есть наши благоприятные исходы из формулы.
Будьте внимательны: иногда в задаче есть указание к округлению. Значит ответ у вас выйдет некрасивый, но вы его «причЕшите» округлением.
Еще один подвох: формулировка с предлогом «на». К примеру, «на 100 лампочек 3 неисправны, найдите вероятность купить неисправную». Подходящие исходы даны тут явно: 3 неисправные лампочки. А вот число всех исходов спрятано и составляет 103, потому что «на».
Всегда есть вероятность, что вам не повезет, и попадется задачка с перебором подходящих вариантов… Тема довольно объемная, можете изучить ее самостоятельно или надеяться на удачу.
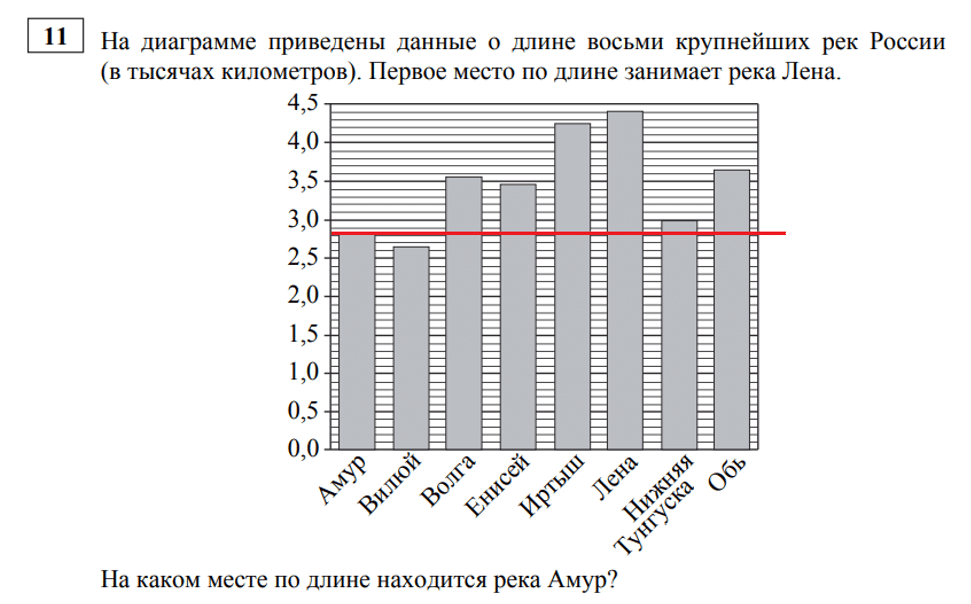
Задание 11 (Делаем обязательно!)
Задание на работу с графиком, диаграммой или таблицей, и не выполнить его вы просто не имеете права! Вооружайтесь карандашом, читайте условие с предельной внимательностью, безжалостно отмечайте нужные по условию значения на картинке в КИМе. Мы серьезно, вы и представить не можете, сколько народу теряет тут баллы по невнимательности.
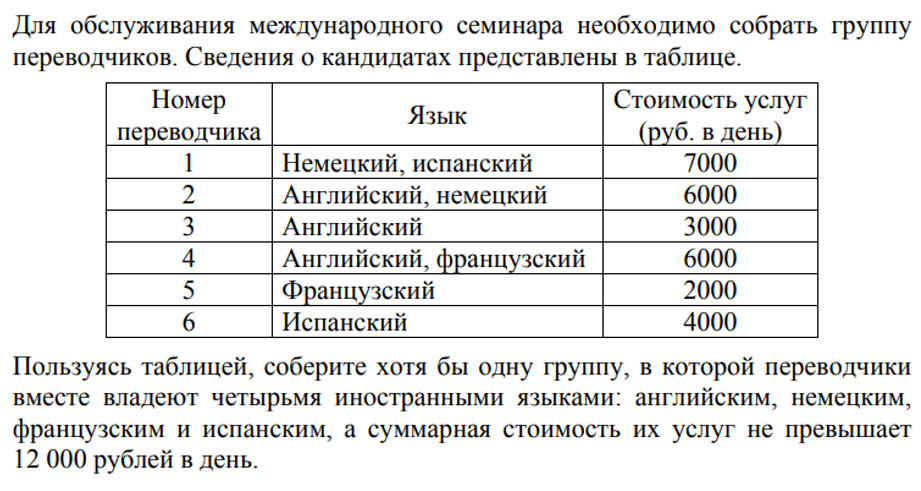
Задание 12 (Делаем обязательно!)
Задание проверяет навык чтения информации из таблицы и подбора подходящего по условию варианта.
Задание 14
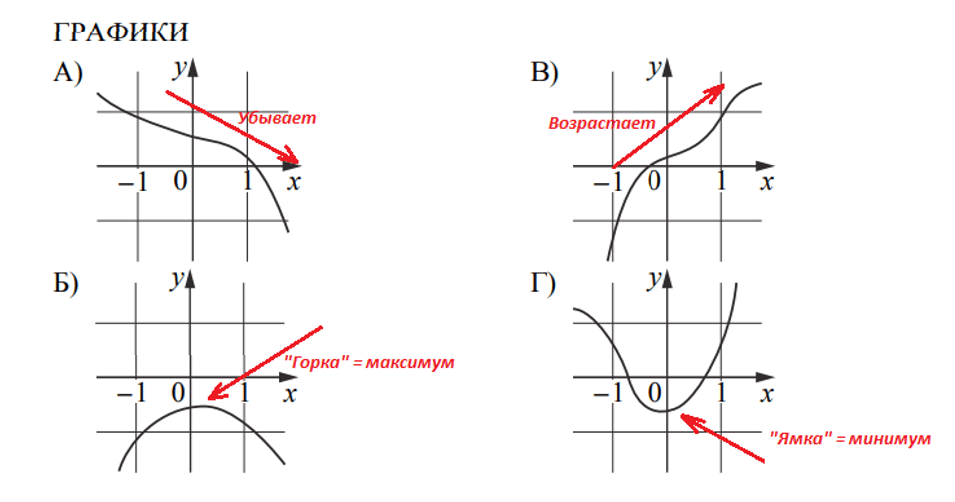
В номере точно понадобится навык анализа поведения функции по графику.
Запомним: точка максимума будет на «горке». Точка минимума — в«ямке». Функция убывает, если идёт вниз слева направо. Возрастает, если идёт вверх слева направо.
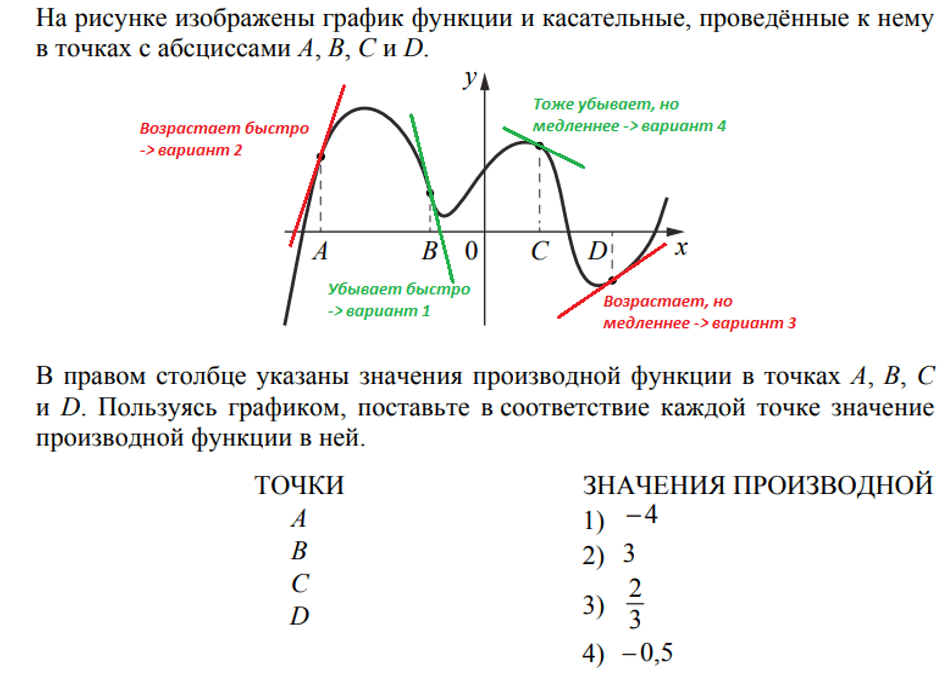
Если не повезет, то придется вспомнить азы теории по производной.
Здесь всё дело в касательных. Нужно внимательно к ним присмотреться. Если касательная к графику возрастает, то значение производной будет положительное, если убывает – отрицательное. Производная будет тем больше по величине (модулю), чем быстрее возрастает или убывает касательная.
Задание 18 (Делаем обязательно!)
Задача проверяет у ребят, которые хотят сдать базовую математику, умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.
Все, что от вас требуется – схематично изобразить на черновике ясень, рябину и осину, указать известную разницу в высоте и внимательно сопоставить картинку с утверждениями.
Важно! Не додумывайте какие-то дополнительные условия, не указанные в тексте задачи. Учитесь читать строго то, что написано.
А бывают случаи, когда с визуализацией задачки придется постараться.
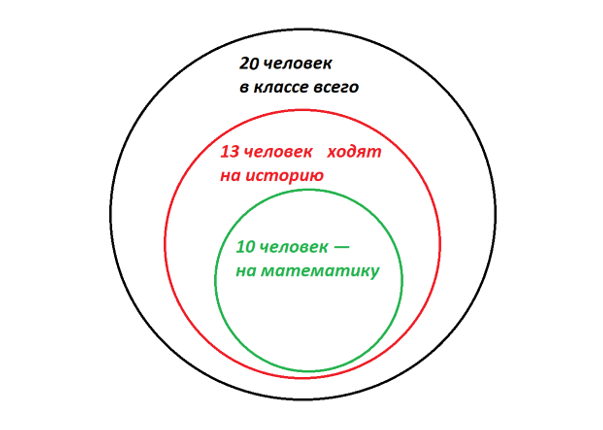
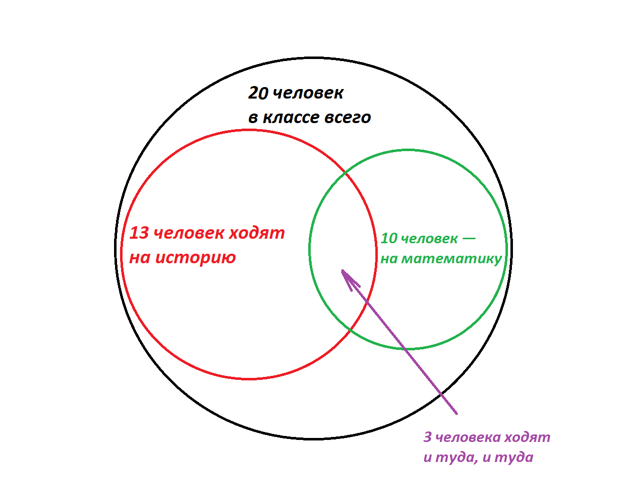
Тут иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет наглядно изобразить множество объектов. В данном случае — школьников. Давайте прикинем, как ребята могут распределиться по кружкам?
Конечно, возможны еще какие-то промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.
Так что для решения иногда мало логики, понадобится еще чуток воображения. Потренируйтесь, и ваши шансы получить балл повысятся.
Задание 19
Чем дальше, тем интереснее становятся задачи. Этот номер уже напоминает олимпиадную задачку, правда для средней школы.
Если хотите сдать базовую математику и решить 19 номер, надо немного познакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте, если время на ЕГЭ позволяет.
Например, тут нам помогут признаки делимости. Отдельного признака для 12 нет, потому нам надо разложить его на разные множители, признак для которых есть. Например, это:
Эти несложные закономерности гугл выдает по первому же запросу. Их немного: на 2, 3, 4, 5, 8, 9, 10, 11. Вполне посильная задача для выпускника.
Начнем с признака для четырех. Пока что наше число заканчивается на 13. На 4 не делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на 61. Тоже не подходит. Вычеркнем еще одну. Теперь на конце 76… Вот оно! От изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать одну.
Теперь проверим признак для трех: 7+5+1+5+7+6 = 31. Какое ближайшее число разделиться на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.
Ответ: 75576. Конечно, это не единственное решение.
А задание такого типа можно попытаться подобрать, расположений не слишком много. Мы все же постараемся порассуждать, чтобы уменьшить количество возможных вариантов.
Чтобы число делилось на 10, оно должно заканчиваться на 0. Например, это получится, если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под условие задачи подойдет 7 + 27 + 356 = 390.
Какие задания мы не разобрали и почему
Теперь вы знаете, как сдать базовую математику, решив семь заданий (или больше, конечно!). Но некоторые номера базового ЕГЭ включают слишком большое разнообразие прототипов и методы решения к ним не ограничиваются парой простых алгоритмов.
Например, в эту группу относятся все задания по геометрии: 8, 13, 15, 16. Чтобы решать геометрию, мало знать основные фигуры и формулы. Необходим навык, который вырабатывается только практикой.
Задание 17 обычно, хоть и не всегда, содержит неравенство. Это отдельный большой блок теории, которую тоже необходимо подкреплять практикой. Но, может, вам повезет, и попадется задачка на расположение значений на числовой прямой.
Тут достаточно примерно прикинуть значения и аккуратно внести ответы в бланк. Ясно, что семь третьих больше двух, но меньше трех. Корень из 26 равен пяти с копейками, а отрицательная степень сделает из трех пятых пять третьих или чуть больше полутора. Подобные задания надо пытаться делать обязательно!
Задание 20. Здесь попадаются разные типы неочевидных задач на логику. Решение каждой нужно рассматривать отдельно и подробно. Если хотите прочитать о том, какие задачи бывают в 20 номере, пишите в комментариях, и Maximum поделится своими методами решения!
Не знаете, какой вуз выбрать? Воспользуйтесь бесплатной консультацией в нашем центре. Что это такое? Все просто: вы расскажете о себе и о своих интересах. А специалист посоветует, на какие специальности обратить внимание, в какой вуз поступать, какие ЕГЭ сдавать. Так вы сэкономите время на подготовку и сможете выбрать образование, которое точно окажется для вас интересным и полезным!