Создание условных формул
Проверка истинного или ложного условия и логические сравнения выражений являются общими для многих задач. Для создания условных формул можно использовать функции И, ИЛИ,НЕ и ЕСЛИ.
Например, функция ЕСЛИ использует следующие аргументы:
Формула, использующая функцию ЕСЛИ
logical_test: условие, которое вы хотите проверить.
value_if_true: значение, возвращаемое, если условие имеет значение Истина.
value_if_false: значение, которое возвращается, если условие имеет значение False.
Дополнительные сведения о создании формул см. в теме Создание и удаление формул.
Что необходимо сделать
Создание условной формулы с логическим значением (ИСТИНА или ЛОЖЬ)
Для этого используйте функции и операторы AND, ORи NOT, как показано в примере ниже.
Пример
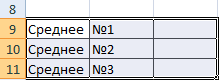
Чтобы этот пример проще было понять, скопируйте его на пустой лист.
Выделите пример, приведенный в этой статье.
Важно: Не выделяйте заголовки строк или столбцов.
Выделение примера в справке
Нажмите клавиши CTRL+C.
В Excel создайте пустую книгу или лист.
Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.
Важно: Чтобы пример правильно работал, его нужно вставить в ячейку A1.
Чтобы переключиться между просмотром результатов и просмотром формул, возвращающих эти результаты, нажмите клавиши CTRL+` (знак ударения) или на вкладке Формулы в группе Зависимости формул нажмите кнопку Показывать формулы.
Скопировав пример на пустой лист, вы можете настроить его так, как вам нужно.
Использование MS Excel при изучении математической логики
В настоящее время применение информационных технологий становится неотъемлемой частью образовательного процесса. Компьютер наиболее полно удовлетворяет дидактическим требованиям и позволяет адаптировать процесс обучения к индивидуальным особенностям учащихся.
Компьютерные технологии активно внедряются в процесс обучения и диагностики, позволяют упростить процесс отработки навыков и умений и оценки знаний учащихся.
В данной работе рассматривается применение табличного процессора MS Excel при изучении основ логики.
В электронных таблицах предусмотрен также графический режим работы, который дает возможность графического представления (в виде графиков, диаграмм) числовой информации, содержащейся в таблице.
В процессе изучения алгебры логики учащиеся знакомятся с такими понятиями как: высказывание, таблицы истинности, логические функции и логические операции. Алгебра логики является разделом математической логики, в которой изучаются методы доказательства истинности (1) или ложности (0) сложных логических конструкций, составленных из простых высказываний, на основе истинности или ложности последних. Для закрепления полученных знаний возможно использование табличного процессора MS Excel и его функций.
Для реализации функций булевой алгебры используются логические функции: ЕСЛИ, И, ИЛИ, НЕ, ИСТИНА и ЛОЖЬ. При работе с функциями в MS Excel используется мастер функций (Вставка 
Функция…), в котором отображается имя функции, ее описание и аргументы.
Рисунок 1. Окно мастера функций
Первоначально следует создать таблицу основных логических операций:
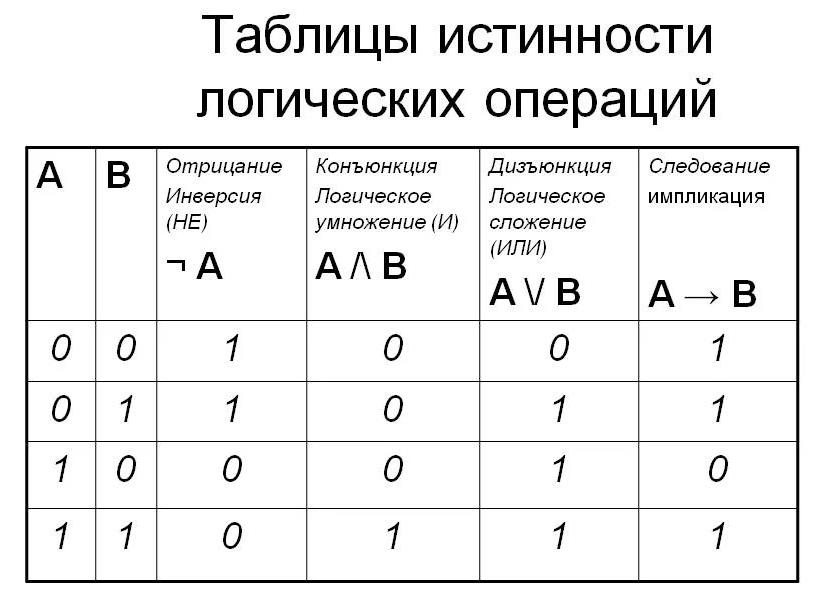
Рисунок 2. Таблица истинности основных логических операций
В последующей работе данная таблица может использоваться учащимися как основа для выполнения заданий лабораторной работы.
Учащимся может быть предложена следующая работа.
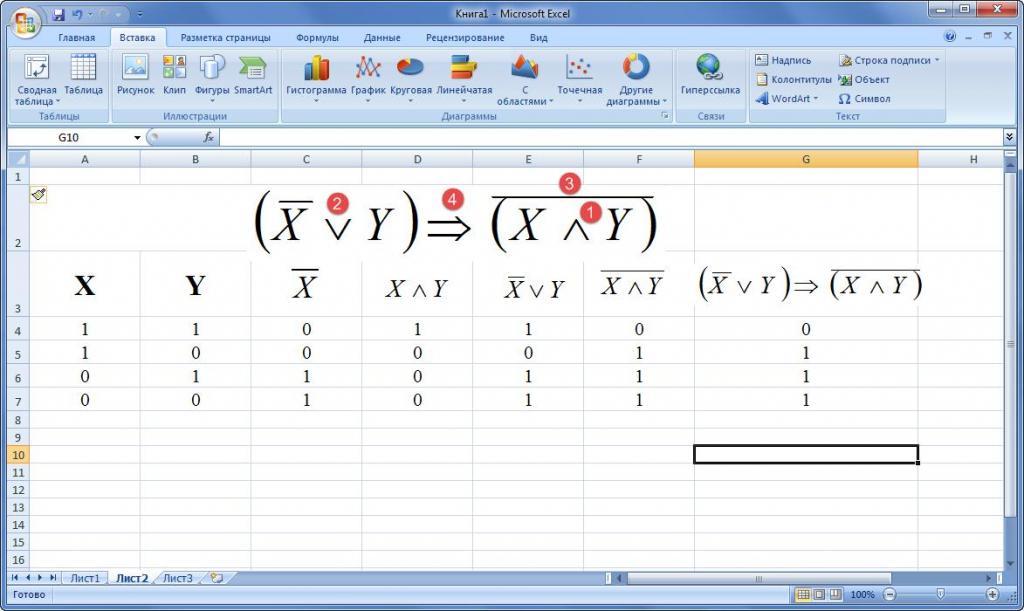
Задание: Построить таблицу истинности для формулы (A 
B 
C) 
A, используя MS Excel.
Рисунок 3. Исходные данные
Для этого в ячейку D2 ввести формулу: =ЕСЛИ(B2=1;0;1);
в E2: =ЕСЛИ(И(A2=1;D2=1);1;0);
в F2: =ЕСЛИ(И(E2=1;C2=0);0;1);
Заполнение остальных строк произвести путем копирования введенной формулы.
Рисунок 4. Результат выполнения работы
Табличный процессор может быть использован для закрепления не только материала математической логики, но и для основ теории вероятностей и математической статистики.
Задачи для самостоятельного решения
Определить с помощью таблиц истинности равносильность формул.
Определить являются ли формулы тавтологиями.
Логические операции в Excel
Логическая – это такая разновидность функции, которая может возвращать одно из возможных значений – истинное, если содержатся внутри ячейки значения, подпадающее под определенный критерий и ложное, если этого не происходит. Используются логические функции с целью программирования электронных таблиц с целью добиться разгрузки себя от часто повторяющихся действий.
Кроме этого, логические функции могут применять с целью проверить, в какой мере содержимое ячейки соответствует определенному критерию. Также могут проверяться и другие логические значения.
Операторы сравнения
Каждое выражение содержит операторы сравнения. Они бывают следующими:
Как следствие, Excel выдает один из двух возможных результатов: истина (1) или ложь (2).
Для применения логических функций необходимо во всех возможных случаях задавать условие, содержащее одно или несколько операторов.
Функция «Истина»
Для использования этой функции не нужно указывать никаких аргументов, и она всегда возвращает «Истина» (что соответствует цифре 1 двоичной системы счисления).
Функция «Ложь»
Функция, полностью аналогичная предыдущей, только возвращаемый ею результат – «Ложь». Самая легкая формула, где можно использовать эту функцию, следующая =ЛОЖЬ().
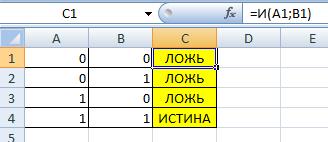
Функция «И»
Задачей этой формулы является возвращение значения «Истина» при соответствии каждого из аргументов определенному значению или определенному критерию, которые описаны выше. Если вдруг возникает несоответствие одного из критериев требуемому, то возвращается значение «Ложь».
Ссылки на ячейки с логическими значениями также применяются в качестве параметров функции. Максимальное количество аргументов, которые можно использовать – 255. Но обязательное требование – наличие хотя бы одного из них в скобках.
| И | Истина | Ложь |
| Истина | Истина | Ложь |
| Ложь | Ложь | Ложь |
Синтаксис этой функции такой:
= И(Логическое значение1; [Логическое значение 2];…)
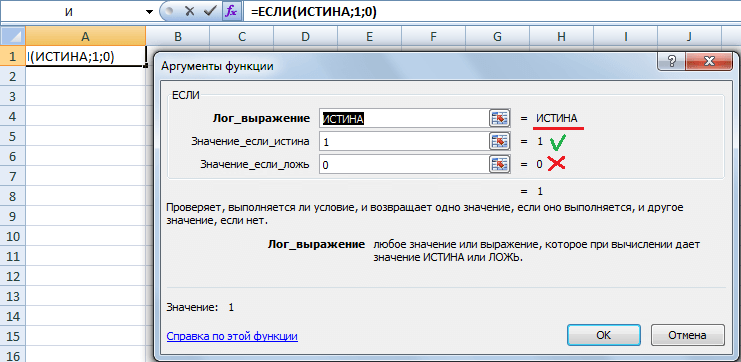
На данном скриншоте видно, что каждый аргумент передает истинное значение, поэтому в результате использования этой формулы можно получить соответствующий результат.
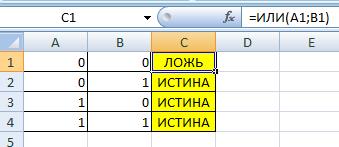
Функция «Или»
Проверяет несколько значений на предмет соответствия определенному критерию. Если какой-то из них соответствует, то функция возвращает истинное значение (1). Максимальное количество аргументов в данной ситуации также равняется 255, и необходимо обязательно указывать один параметр функции.
| ИЛИ | Истина | Ложь |
| Истина | Истина | Истина |
| Ложь | Истина | Ложь |
Синтаксис формулы следующий:
=ИЛИ(Логическое значение 1; [Логическое значение 2];…)
Точно так же, как в предыдущем и последующем случае, каждый аргумент должен быть отделенным от другого с помощью точки с запятой. Если обратиться к приведенному выше примеру, то там каждый параметр возвращает «Истина», поэтому если необходимо при обращении к этому диапазону применять функцию «ИЛИ», то формула вернет «Истина» до тех пор, пока один из параметров не будет соответствовать определенному критерию.
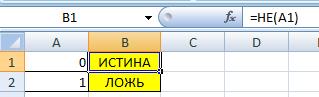
Функция «Не»
Ею возвращаются те значения, которые являются противоположными по отношению к изначально заданному. То есть, при передаче в качестве параметра функции значения «Истина», вернется «Ложь». Если же соответствия не обнаружено, то «Истина».
То, какой результат будет выдан, зависит от того, какой исходный аргумент принимается функцией. Если, например, применять функцию «И» вместе с функцией «НЕ», то таблица будет следующей.
| НЕ(и()) | ИСТИНА | ЛОЖЬ |
| ИСТИНА | ЛОЖЬ | ИСТИНА |
| ЛОЖЬ | ИСТИНА | ИСТИНА |
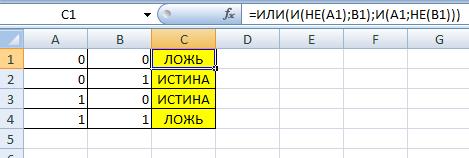
При использовании же функции «Или» в сочетании с функцией «Не», то таблица обретет такой вид.
| НЕ(ИЛИ()) | ИСТИНА | ЛОЖЬ |
| ИСТИНА | ЛОЖЬ | ЛОЖЬ |
| ЛОЖЬ | ЛОЖЬ | ИСТИНА |
Синтаксис этой функции очень прост: =НЕ(принимаемое логическое значение).
Эта функция по праву может называться одной из наиболее востребованных. Она проверяет определенное выражение на предмет соответствия конкретному условию. На результат влияет истинность или ложность данного утверждения.
Если говорить конкретно про эту функцию, то ее синтаксис будет несколько сложнее.
=ЕСЛИ(Логическое_выражение;[Значение_если_истина];[Значение_если_ложь]) 
Пользователь может вкладывать одну функцию ЕСЛИ в другую. Это необходимо делать в тех случаях, когда в результате одной проверки на предмет соответствия определенному условию приходится делать еще одну.
=ЕСЛИ(ЛЕВСИМВ(A2;4)=»1111″; «Visa»;ЕСЛИ(ЛЕВСИМВ(A2;4)=»2222″;»Master Card»;»карта не определена»))
Аналогично можно добиться приличной вложенности и проверять содержимое ячейки или диапазона на предмет соответствия нескольким условиям.
Функция ЕСЛИОШИБКА
Необходима для того, чтобы определить, если ли ошибка. Если да, то возвращается значение второго аргумента. Если же все в порядке, то первого. Всего функция имеет два аргумента, каждый из которых обязательный.
Эта формула имеет следующий синтаксис:
Как можно использовать функцию?
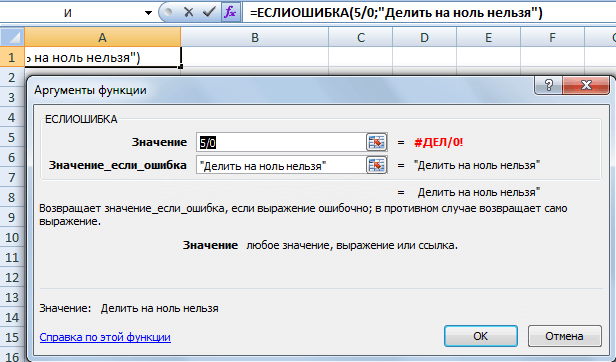
В примере, приведенном ниже, видна ошибка в первом аргументе функции. Поэтому формула возвращает ответ, что запрещено деление на ноль. Первым параметром функции могут быть любые другие формулы. Человек может самостоятельно решать, какое содержимое может быть там. 
Как могут использоваться логические функции на практике
Задача 1
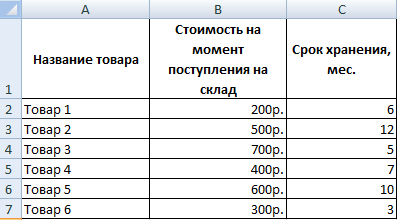
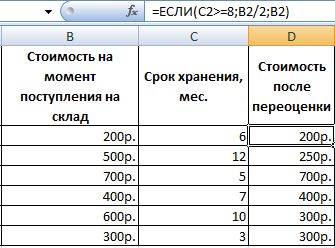
Перед человеком поставлена цель осуществить переоценку товарных остатков. В случае хранения продукта в течение большего, чем 8 месяцев периода, необходимо снижать его стоимость в два раза.
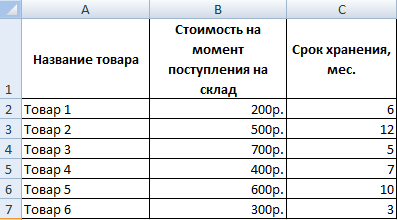
Изначально нужно сформировать такую таблицу. 
Логическое выражение, содержащееся в первом аргументе функции, составлено с использованием операторов > и =. Простыми словами, изначально критерий следующий: при значении ячейки, большем или равном 8, выполняется формула, поставленная во втором аргументе. Выражаясь терминологическим языком, если первое условие оказывается истинным, то выполняется второй аргумент. Если же ложным – третий. 
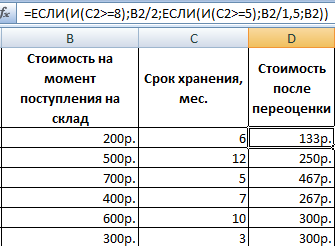
Сложность этой задачи может быть увеличена. Предположим, что перед нами стоит задача использовать логическую функцию И. В этом случае условие обретет следующий вид: в случае хранения продукции в течение большего, чем 8 месяцев срока, то его цену необходимо сбросить в два раза. Если же он находится на реализации больше 5 месяцев, то необходимо сбрасывать в 1,5 раза.
В этом случае необходимо в поле ввода формулы ввести такую строку.
=ЕСЛИ(И(C2>=8);B2/2;ЕСЛИ(И(C2>=5);B2/1,5;B2)) 
Функция ЕСЛИ допускает использование текстовых строк в аргументах, если это требуется.
Задача 2
Если же условие не выполняется (то есть, оказывается ложным), то формула автоматически возвращает пустое значение. Таким образом, если товар был продан ранее или лежит на складе меньше, чем необходимо, или он был уценен до значения, меньше порогового, то остается пустая ячейка.
Допускается применение и других функций как аргументов. Например, допустимо использование математических формул.
Задача 3
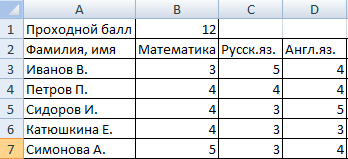
Предположим, есть несколько учеников, которые перед поступлением в гимназию сдают несколько экзаменов. В качестве проходного балла стоит оценка в 12. А чтобы поступить, обязательно необходимо, чтобы стояло хотя бы 4 балла по математике. В результате, Excel должен составить отчет о поступлении.
Для начала необходимо построить следующую таблицу. 
Наша задача – сравнить сумму всех оценок с проходным баллом, а кроме этого убедиться, чтобы оценка по математике была ниже 4. И в графе с результатом необходимо указать «принят» или «нет».
Нам необходимо ввести следующую формулу.
Таким образом, с помощью функции ЕСЛИ можно решать множество различных задач, поэтому она является одной из наиболее часто встречаемых.
Задача 4
Предположим, перед нами появляется необходимость понять, сколько стоят товары после оценки в целом. Если стоимость продукта оказывается ниже, чем среднее значение, то необходимо списать этот товар.
Для этого можно использовать ту же таблицу, которая была приведена выше. 
Чтобы решить эту задачу, необходимо использовать такую формулу.
Задача 5
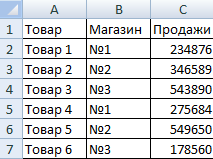
В этом случае, допустим, нам необходимо определить средние продажи. Для этого необходимо составить такую таблицу. 
Далее следует вычислить среднее значение тех ячеек, содержимое которых соответствует определенному критерию. Таким образом, необходимо использовать как логическое, так и статистическое решение. Под приведенной выше таблицей нужно составить вспомогательную, в которой будут отображаться результаты. 
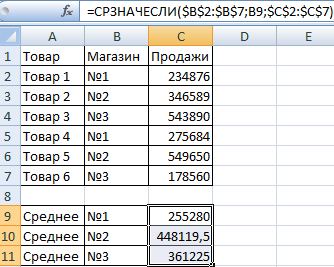
Эта задача может быть решена с использованием всего лишь одной функции.
В качестве первого аргумента используется диапазон значений, которые будут проверяться. Во втором указывается условие, в нашем случае это ячейка B9. А вот в качестве третьего аргумента используется диапазон, который будет применяться для того, чтобы осуществлять расчет среднего арифметического значения.
Функция СРЗНАЧЕСЛИ позволяет сравнить значение ячейки B9 с теми значениями, которые располагаются в диапазоне B2:B7, где перечисляются номера магазинов. Если данные совпадают, то формула подсчитывает среднее арифметическое диапазона C2:C7. 
Выводы
Также были приведены несколько примеров, как можно использовать логические функции в реальных ситуациях.
Существует еще множество аспектов применения логических функций, но тяжело их все рассмотреть в рамках одной, пусть даже большой, статьи. Нет предела совершенству, поэтому всегда можно искать новые варианты применения уже известных формул.
Построить таблицу истинности в Excel: основные понятия и примеры
Алгебра высказываний – точная наука, не дающая компромиссов. Чтобы решить примеры с конъюнкцией, дизъюнкцией, импликацией и т. д., можно построить таблицу истинности в прикладной программе Excel. Она оснащена набором логических функций, позволяющих автоматизировать и облегчить процесс нахождения результата.
Математическая логика: основные понятия
Основателем формальной логики считают Аристотеля. В XVII в. Г. Лейбниц предложил вводить символы для определения высказываний. Д. Буль закрепил усвоенные знания и впервые обозначил предложения символами.
Вам будет интересно: Значение выражения «спустить на тормозах»
Схематически «ИСТИНА» замещается 1, а «ЛОЖЬ» – 0.
Под высказыванием понимают любое повествовательное предложение, дающее какую-либо информацию и способное принимать значение истинности или ложности. В алгебре логики отвлекаются от смысловой нагрузки предложений и рассматривают только логические значения.
Под отрицанием понимают новое выражение, принимающее значение истины в случае его ложности и наоборот.
Конъюнкцией двух переменных называют новое предложение, принимающее значение истинности в случае одновременного обозначения «1» и ложности в остальных ситуациях.
Под дизъюнкцией двух высказываний понимают новое выражение, принимающее значение «ЛОЖЬ» только при одновременном наличии «0» и «ИСТИНА» в остальных вариациях.
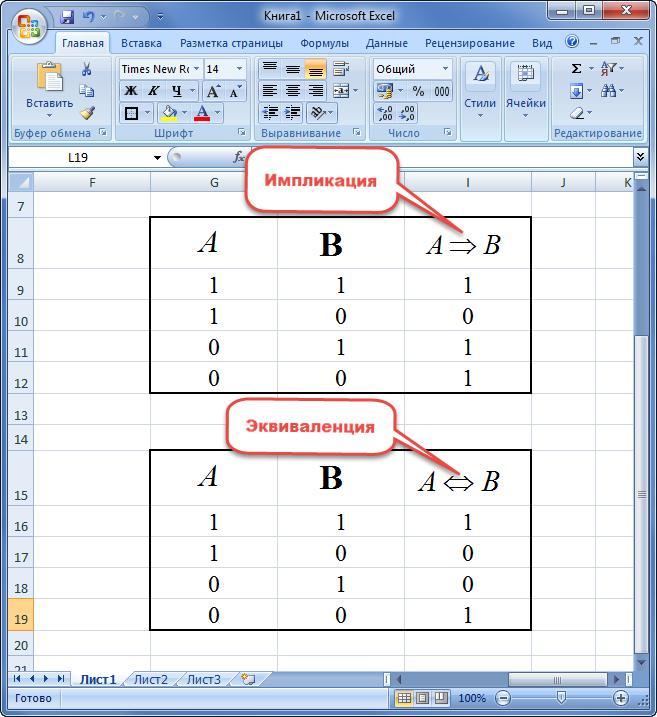
Импликацией двух переменных называют новое предложение, в котором:
Под эквиваленцией двух переменных понимают новое высказывание, принимающее значение истинности только в случае одинаковости элементов. Иначе предложение равняется «0».
Логические значения выражений принято оформлять в табличном виде. Есть и другое название у такого рода информации. Говорят, для высказывания нужно построить таблицу истинности. В ней указываются первоначальные значения для всех переменных, а потом вычисляется результат всего выражения.
Алгоритм реализации вычислений в логических операциях
Чтобы построить таблицу истинности, необходимо знать, в каком порядке выполняются действия. В выражении, где несколько операндов, вычисление осуществляется в следующем порядке:
Существуют еще две операции, но для них приоритет не определен:
Алгоритм вычислений меняется, если выражение заключено в скобки.
Порядок построения табличной формы для логических операндов в Excel
Прежде чем находить значение выражения, нужно изучить понятие формулы алгебры логики. Определение гласит, что это сложное выражение, состоящее из простейших высказываний, соединенных между собой логическими операндами.
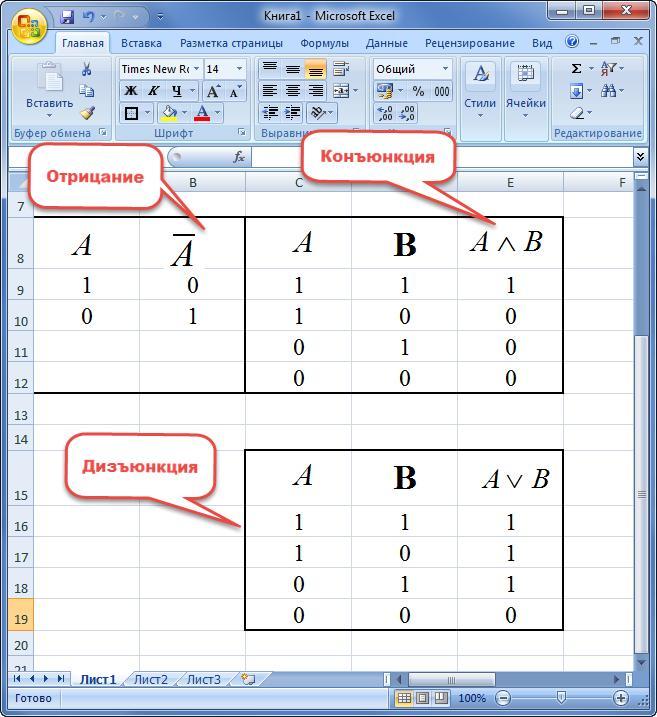
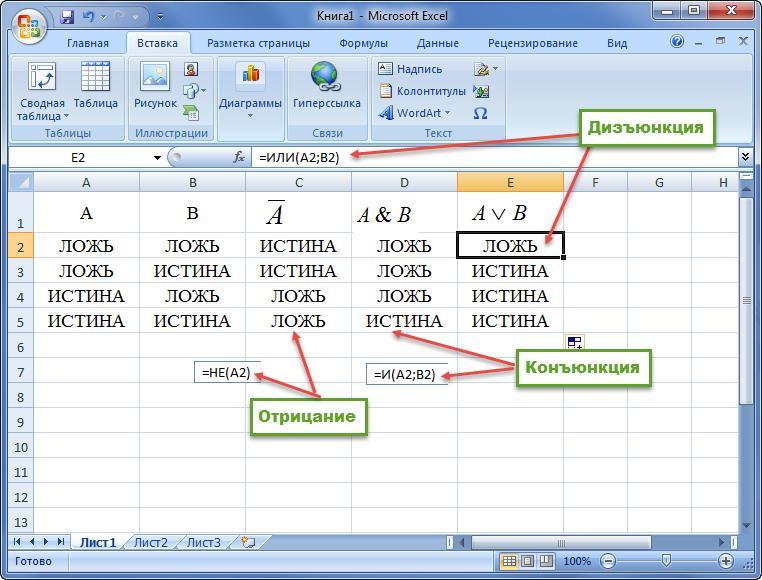
Пример 1. Построить таблицу истинности для конъюнкции, дизъюнкции и отрицания.
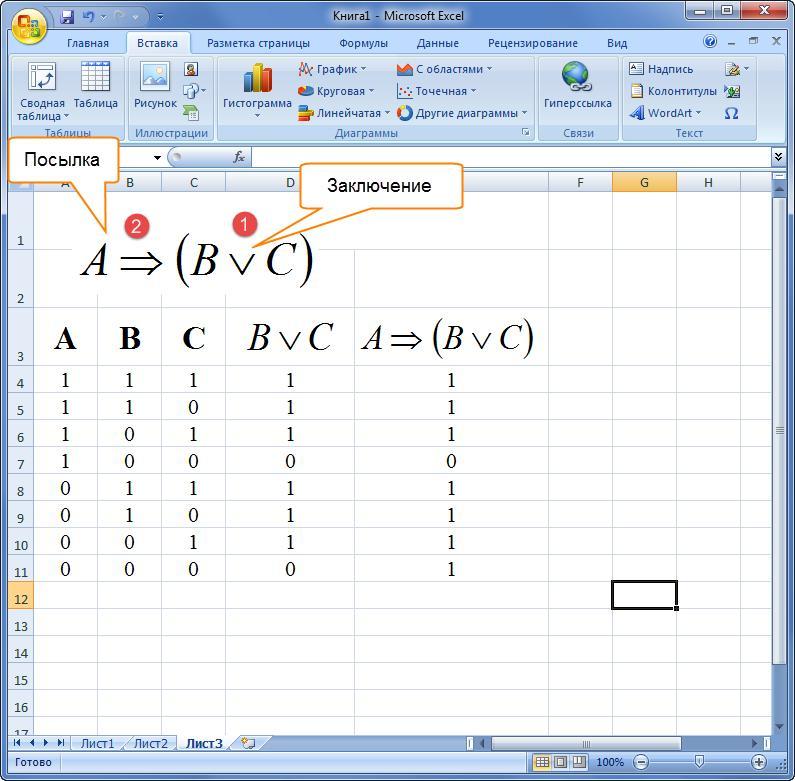
Пример 2. Дана формула алгебры логики. Построить таблицу истинности. Примеры в качестве образца даны ниже.
Пример 3. Как построить таблицу истинности в Excel, если дана формула алгебры логики в словесном описании. Высказывание: «Если треугольник – равносторонний, то все его ребра равны или все его углы равны».
Для начала необходимо разобрать составное предложение на минимальные элементы:
После этого составляется выражение и решается в программном пакете Excel.
При составлении таблиц истинности важно помнить о порядке выполнения операций.
Используем Excel для построения таблицы истинности
Вроде простая вещь — нужно вычислить результат для нескольких булевых переменных
Читаем основную статью
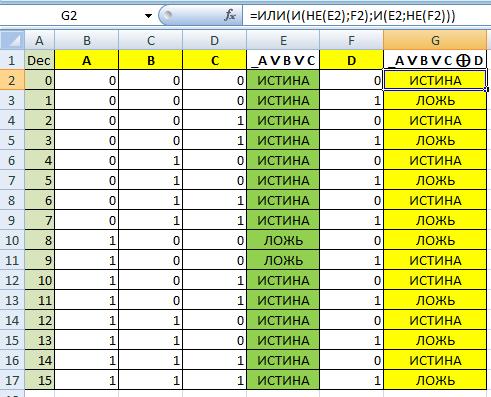
Вроде всё просто. Но вот такой пример вида _A ∨ B ∨ C ⊕ D
Переводим на русский язык (с матемитического) — нужно сделать таблицу истинности для выражения
не A или B или C иск.или D
для всех вариантов переменных A,B.C.D, которые могут принимать значения «Истина» / «Ложь»
Или на английском (для программирования) = not.A.or.B.or.C.xor.D
Задача на булеву алгебру не сложная — но у нас четыре переменных и 16 строк в таблице (да, 2 4 = 16). А если таких переменных будет 5, то в таблице будет 32 строки.
Но у нас есть Excel ( Ex ecute Cel l), который прекрасно понимает формулы логики. Достаточно правильно написать формулу для одной строки — и потом мышкой перетащить эту формулу на остальные строки. Готово!
Логическая операция И
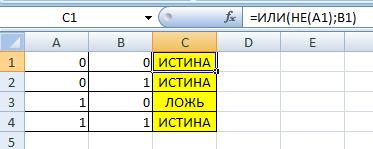
Логическая операция ИЛИ
Логическая операция отрицания (инверсия)
Логическая операция XOR (исключающее ИЛИ)
В Excel 2007 её нет, в более современных версиях она есть. Но мы её соберем сами.
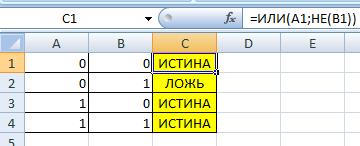
Логическая связка Импликация (прямая)
A → B
используем аналог _A V B
Логическая связка Импликация (обратная)
A ← B
используем аналог A V _B
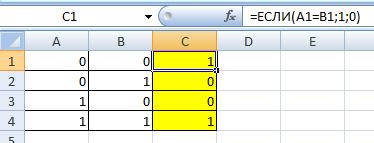
Логическая связка ТОЖДЕСТВО
Собираем таблицу истинности
Не обязательно собирать всё в одной ячейке. Можно сделать столбцы для промежуточных вычислений.
Для нашего примера _A ∨ B ∨ C ⊕ D
Вы можете сохранить ссылку на эту страницу себе на компьютер в виде htm файла
Вы будете видеть наш сайт у себя в ленте
Нажмите «Нравится» или напишите сообщение