Прочитайте, употребив числительные и существительные в нужной форме, следите за правильным произношением?
Прочитайте, употребив числительные и существительные в нужной форме, следите за правильным произношением.
1) К 345 прибавить 157.
2) От 964 отнять 89.
4) Предложение принято 375 (голос) против 44 (голос).
5) деревня находится в 163 (километр) от города.
6) Проведен социологический опрос среди 600 (руководитель) средних и крупных предприятий.
7) 88, 9 % (руководитель) поддержали реформы.
8) Более 51 % (опрошенный) высказались «за».
9) За истекший год было собрано более 580 тысяч тонн зерна.
10) Более 2500 человек обратились за помощью.
11) Прибыл поезд с 287 экскурсантами.
12) Длина окружности равна 422 (сантиметр).
13) Из 596 вычесть 387.
14) Высота Останкинской башни со стальной антенной равна 540 метрам 74 сантиметрам.
15) Самые быстрые бегуны мира развивают скорость от 36 до 43 километров в час.
16) К 1778 прибавить 852.
17) От 17464 отнять 11090.
18). Из 1109 важнейших объектов было введено лишь 749.
19) Сметная стоимость второй очереди канала составляет более 455 миллионов.
1) К трёмстам сорока пяти прибавить сто пятьдесят семь.
2) От девятисот шестидесяти четырёх отнять восемьдесят девять.
3) Десять сложить с семьюстами девяноста восьмью.
4) Предложение принято тремястами семьюдесятью пятью голосами против сорока четырёх голосов.
5) Деревня находится в ста шестидесяти трёх километрах от города.
6) Проведен социологический опрос среди шестисот руководителей средних и крупных предприятий.
7) Восемьдесят восемь целых и девять десятых процента руководителей поддержали реформы.
8) Более пятидесяти одного процента опрошенных высказались «за».
9) За истекший год было собрано более пятисот восьмидесяти тысяч тонн зерна.
10) Более двух тысяч пятисот человек обратились за помощью.
11) Прибыл поезд с двумястами восьмьюдесятью семью экскурсантами.
12) Длина окружности равна четыремстам двадцати двум сантиметрам.
13) Из пятисот девяноста шести вычесть триста восемьдесят семь.
14) Высота Останкинской башни со стальной антенной равна пятистам сорока метрам семидесяти четырём сантиметрам.
15) Самые быстрые бегуны мира развивают скорость от тридцати шести до сорока трёх километров в час.
16) К одной тысяче семистам семидесяти восьми прибавить восемьсот пятьдесят два.
17) От семнадцати тысяч четырёхсот шестидесяти четырёх отнять одиннадцать тысяч девяносто.
18) Из одной тысячи ста девяти важнейших объектов было введено лишь семьсот сорок девять.
19)Сметная стоимость второй очереди канала составляет более четырёхсот пятидесяти пяти миллионов.
12. Пропишите числительные?
12. Пропишите числительные.
Газеты сообщили, что за истекший год было собрано более 580 тысяч тонн зерна.
Из 596 вычесть 387 получится 209.
Прочитайте просклоняйте сочетания количественных числительных с существительными 11 метров 20 километров 4 сантиметра?
Прочитайте просклоняйте сочетания количественных числительных с существительными 11 метров 20 километров 4 сантиметра.
2. Выберите из данных в скобках нужную форму, запишите получившиеся словосочетания, объясните свой выбор 1?
2. Выберите из данных в скобках нужную форму, запишите получившиеся словосочетания, объясните свой выбор 1.
4. СКВ (принималась – принималось – принимался).
5. (Обновленный – обновленная) МКАД.
6. ФИДЕ (объявил – объявила).
3. Запишите, передавая числа словами, употребив числительные и существительные нужной форме 1.
К 345 прибавить 157.
2. От 964 отнять 89.
3. 10 сложить с 798.
4. Предложение принято 375 (голос) против 44 (голос).
5. Деревня находится в 163 (километр) от города.
4. Объясните, как грамматические особенности данных ниже слов или какое их значение обусловливают возможность употреблять с ними : а) только количественные числительные (два, три, четыре) ; б) только собирательные числительные (двое, трое, четверо) ; в) обе формы Сын, пароход, командир, директор, батрак, воз, сани, сутки, дочь, учительница, батрачка, деревня, село, город, преподаватель, педагог, медведь, зверь, волк, они, военный.
Какое слово из етих существительное метр тонна сантиметр килограмм центнер километр децеметр грамм?
Какое слово из етих существительное метр тонна сантиметр килограмм центнер километр децеметр грамм.
Запишите предложения, заменяя цифры словами и, где нужно, раскрывая скобки?
Запишите предложения, заменяя цифры словами и, где нужно, раскрывая скобки.
1. Газеты сообщали, что за истекший год было собрано более 580 тысяч тонн зерна.
2. Прибыл поезд с 287 экскурсантами.
3. Высота башни со стальной трубчатой антенной равна 540 метрам 74 сантиметрам
Корпорация провела социологический опрос среди 600(руководитель) предприятий России.
5. Год приблизительно равен 365(сутки)
7. (обоим, обеим) ученицам дали дополнительное задание
(Пятеро, пять) автомобилей закончили гонку
Поселок находится в (1, 5 километр) от города
Гроссмейстер провел сеанс одновременной игры на (полтораста досок).
Спишите, заменяя цифры словами?
Спишите, заменяя цифры словами.
Определите падеж числительных.
К 5 прибавить 2, к 2 прибавить 4, от 15 отнять 9, к 6 часам утра, между 5 и 10 часами утра, к 11 прибавить 13, от 30 отнять 13, с 20 часов до 4 часов ночи, между 20 и 12 часами, к 1 прибавить 6.
Запишите предложения употребив числительные в нужном падеже (предложение принято 789 против 678 голосов?
Запишите предложения употребив числительные в нужном падеже (предложение принято 789 против 678 голосов.
НУЖНО НАПИСАТЬ СЛОВАМИ?
НУЖНО НАПИСАТЬ СЛОВАМИ!
К 631 прибавить 562.
Если от 976 вычесть 382 то получится 594.
К 468 прибавить 617.
Длина окружности равна 422 сантиметрам заменить словами эти числительные?
Длина окружности равна 422 сантиметрам заменить словами эти числительные.
На уроке математике?
На уроке математике.
Письменно выполните арифметические действия, заменяя цифры словами.
. 3. 900 разделить на 300, будет.
. 4. К 400 прибавить 500, получится.
Длина окружности
6 класс, 9 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен 
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
«Трёхсот» или «трёхста» как пишется?
Если у вас возникли трудности с выбором правильного варианта между словами «трёхсот» и «трёхста», то прежде всего необходимо обратить внимание на разряд числительного и на его вид по структуре.
Как правильно пишется
Согласно правилам русского языка, верным вариантом написания этого числительного будет слово «трёхсот».
Какое правило применяется
Начальной формой числительного «трёхсот» является слово «триста». «Триста» – количественное числительное, отвечающее на вопрос «сколько» и, соответственно, обозначающее количество.
Все количественные числительные по своей структуре делятся на три вида: простые (имеют один корень), составные (состоят из двух и более слов) и сложные (имеют два корня). Для того чтобы определить, каким числительным является «триста», необходимо просклонять его по падежам: «триста», «тремястами», «трёмстам». Видим, что общей частью являются корни «тр» и «ст», а значит, «триста» – это сложное числительное.
По правилам русского языка, у сложных количественных числительных при склонении меняются обе части.
| Именительный падеж | триста |
| Родительный падеж | трёхсот |
| Дательный падеж | трёмстам |
| Винительный падеж | триста |
| Творительный падеж | тремястами |
| Предложный падеж | о трёхстах |
Интересуемое нас слово «трёхсот» – это форма Родительного падежа. Однако почему же именно «трёхсот», а не «трёхста»?
Дело в том, что очень часто это сложное числительное путают с простым – «сто», которое имеет только две формы: «ста» и «сто». Но если корень «ст» входит в состав сложного существительного, то он склоняется иначе.
Примеры предложений
Как неправильно писать
Ни в коем случае нельзя писать это числительное с окончанием «а» во второй части – «трёхста».
Склонение 300 по падежам
Число 300 прописью: триста.
Количественное числительное 300
| Падеж | Вопрос | 300 |
|---|---|---|
| Именительный | есть что? | триста рублей |
| Родительный | нет чего? | трёхсот рублей |
| Дательный | рад чему? | трёмстам рублям |
| Винительный | вижу что? | триста рублей |
| Творительный | оплачу чем? | тремястами рублями |
| Предложный | думаю о чём? | о трёхстах рублях |
Порядковое числительное 300
| Падеж | Вопрос | мужской род | женский род | средний род | мн.число |
|---|---|---|---|---|---|
| Именительный | какой? | трёхсотый | трёхсотая | трёхсотое | трёхсотые |
| Родительный | какого? | трёхсотого | трёхсотой | трёхсотого | трёхсотых |
| Дательный | какому? | трёхсотому | трёхсотой | трёхсотому | трёхсотым |
| Винительный | какой? | трёхсотый | трёхсотую | трёхсотое | трёхсотые |
| Творительный | каким? | трёхсотым | трёхсотой | трёхсотым | трёхсотыми |
| Предложный | о каком? | трёхсотом | трёхсотой | трёхсотом | трёхсотых |
Примечание. В винительном падеже окончание зависит от одушевлённости/неодушевлённости объекта. В мужском роде используется трёхсот ый для неодушевлённых и трёхсот ого для одушевлённых. Во множественном числе используется трёхсот ые для неодушевлённых и трёхсот ых для одушевлённых.
Длина окружности
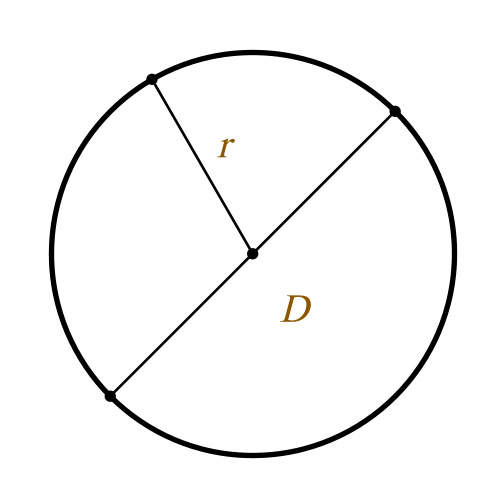
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.
Определение длины окружности
Формула расчёта длинны окружности
Произвести расчёт окружности можно по следующей формуле:
r – радиус окружности
D – диаметр окружности
L – длина окружности
Пример нахождения длинны окружности
Вычислить длину окружности, имеющей радиус 10 сантиметров.
Формула для вычисления дины окружности имеет вид:
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 31,4 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.