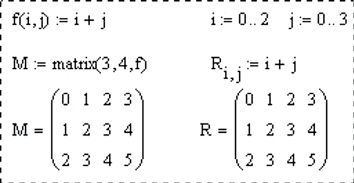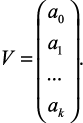Как пишется котангенс в маткаде
Этот раздел описывает тригонометрические, гиперболические и показательные функции Mathcad вместе с обратными им. Здесь также описываются встроенные функции Бесселя.
Тригонометрические функции и обратные им.
Тригонометрические функции Mathcad и обратные им определены для любого комплексного аргумента. Они также возвращают комплексные значения везде, где необходимо. Результаты для комплексных значений вычисляются с использованием тождеств:
Для применения этих функций к каждому элементу вектора или матрицы используйте оператор векторизации.
Обратите внимание, что все эти тригонометрические функции используют аргумент, выраженный в радианах. Чтобы перейти к градусам, используется встроенная единица deg. Например, чтобы вычислить синус 45 градусов, введите sin(45*deg).
Имейте в виду, что из-за ошибок округления, свойственных машинной арифметике, Mathcad может возвращать очень большое число в той точке, где находится особенность вычисляемой функции. Вообще, необходимо быть осторожным при вычислениях в окрестности таких точек.
| asin(z) | Возвращает угол (в радианах), чей синус — z. |
| acos(z) | Возвращает угол (в радианах), чей косинус — z. |
| atan(z) | Возвращает угол (в радианах), чей тангенс — z. |
Гиперболические функции sinh и cosh определяются формулами:
Эти функции также могут использовать комплексный аргумент и возвращать комплексные значения. Гиперболические функции тесно связаны с тригонометрическими функциями. Справедливы формулы:
sinh(i


| sinh (z) | Возвращает гиперболический синус z. |
| cosh (z) | Возвращает гиперболический косинус z. |
| tanh (z) | Возвращает sinh(z)/cosh(z), гиперболический тангенс z. |
| csch (z) | Возвращает 1/sinh(z), гиперболический косеканс z. |
| sech (z) | Возвращает 1/cosh(z), гиперболический секанс z. |
| coth (z) | Возвращает 1/tanh(z), гиперболический котангенс z. |
| asinh (z) | Возвращает число, чей гиперболический синус — z. |
| acosh (z) | Возвращает число, чей гиперболический косинус — z. |
| atanh (z) | Возвращает число, чей гиперболический тангенс — z. |
Логарифмические и показательные функции
Логарифмические и показательные функции Mathcad могут использовать комплексный аргумент и возвращать комплексные значения. Значения экспоненциальной функции для комплексного аргумента вычисляются с применением формулы
e x+iy =e x (cos(y) + i
Вообще говоря, значения натурального логарифма даются формулой
ln(x + i





В Mathcad функция ln возвращает значение, соответствующее n = 0. А именно:
ln(x + i


Оно называется основным значением логарифма. Рисунок 1 иллюстрирует некоторые основные свойства логарифма.
| exp(z) | Возвращает e в степени z. |
| ln(z) | Возвращает натуральный логарифм z. (z 0). 0). |
| log(z) | Возвращает логарифм z по основанию 10. (z 0). 0). |
На Рисунке 1 показано, как можно использовать эти функции для вычисления логарифма по любому основанию.
Рисунок 1: Использование логарифмических функций.
Эти функции обычно возникают как решения для волнового уравнения, подчиненного цилиндрическим граничным условиям.
Функции Бесселя первого и второго рода, Jn(x) и Yn(x), являются решениями для дифференциального уравнения
Модифицированные функции Бесселя первого и второго рода, In(x) и Kn(x), являются решениями для немного видоизмененного уравнения:
| J0(x) | Возвращает J0(x); x вещественный. |
| J1(x) | Возвращает J1(x); x вещественный. |
| Jn(m, x) | Возвращает Jn(x); x вещественный, 0 m m 100. 100. |
| Y0(x) | Возвращает Y0(x); x вещественный, x > 0. |
| Y1(x) | Возвращает Y1(x); x вещественный, x > 0. |
| Yn(m, x) | Возвращает Yn(x). x > 0, 0 m m 100 100 |
| I0(x) | Возвращает I0(x); x вещественный. |
| I1(x) | Возвращает I1(x); x вещественный. |
| In(m, x) | Возвращает In(x); x вещественный, 0 m m 100. 100. |
| K0(x) | Возвращает K0(x); x вещественный, x > 0. |
| K1(x) | Возвращает K1(x); x вещественный, x > 0. |
| Kn(m, x) | Возвращает Kn(x). x > 0, 0 m m 100 100 |
Следующие функции возникают в широком круге задач.
x должен быть вещественным.
Гамма-функция Эйлера удовлетворяет рекуррентному соотношению
Откуда следует для положительных целых z:
Интеграл ошибок часто возникает в статистике. Он может также быть использован для определения дополнения интеграла ошибок по формуле:
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Встроенные операторы и функции Mathcad
Таблица ПЗ.1. Арифметические операторы
Вычитание или отрицание (унарная операция)
Матричное умножение, умножение на скаляр
Скобки (изменение приоритета)
Возведение в степень n
Возведение матрицы в степень n
Скалярные операции над векторами и матрицами, если это не оговорено особо, производятся независимо над их каждым элементом, как над скаляром.
Таблица П3.2. Вычислительные операторы
Вычисление n-й производной
Сумма ранжированной переменной
Произведение ранжированной переменной
Таблица ПЗ.З. Встроенные функции по алфавиту
Обратная тригонометрическая или гиперболическая функция *
Функция Эйри первого рода
х,у — координаты точки
Угол между точкой и осью ОХ
file— строковое представление пути к файлу
Дозапись данных в существующий текстовый файл
z — аргумент функции
Аргумент комплексного числа
х,у — координаты точки
Угол, отсчитываемый от оси ОХ до точки (х,у)
А,В,С. — векторы или матрицы
Слияние матриц слева направо
n — порядок х — аргумент
Мнимая и действительная части функции Бесселя —Кельвина
Функция Эйри второго рода
х,у — векторы данных
и — вектор значений сшивок В-сплайнов
n — порядок полиномов
Вектор коэффициентов В-сплайна
Bulstoer (y0, t0, t1, M, D)
Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера
bulstoer (y0, t0, t1, acc, D, k, s)
Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера (для определения только последней точки интервала)
Bvalf it (z1, z2, x0, x1, xf, D, load1, load2, score)
zl,z2 — вектор начальных значений для недостающих левых и правых граничных условий
хО — левая граница xl — правая граница xf — внутренняя точка
D(x,y) — векторная функция, задающая систему ОДУ
Возвращает вектор недостающих граничных условий у краевой задачи для системы N ОДУ с дополнительным условием в промежуточной точке
Наименьшее целое, не меньшее х
Вектор прямого комплексного преобразования Фурье (в разных нормировках)
А — квадратная, определенная матрица
А — матрица или вектор
Объединение строковых переменных
А — квадратная матрица
Числа обусловленности в разных нормах (Ы, L2, Евклидова, »)
А — матрица i — индекс столбца
Сортировка строк матрицы по элементам 1-го столбца
CreateMesh (F, s0, s1, t0, t1, sgr, tgr, fmap)
tO.tl — пределы! sO.sl — пределы s
tgr, sgr — число точек сетки по t и s
fmap— функция преобразования координат
Cre-ateSpace(F[, t0, t1, tgr, fmap])
F(t) — векторная функция из трех элементов
tgr — число точек сетки по t
fmap— функция преобразования координат
Комплексный знак числа
х,у — векторы данных
Вектор коэффициентов кубического сплайна
r,6,z— цилиндрические координаты
Преобразование цилиндрических координат в прямоугольные
х— значение случайной величины
par — список параметров распределения *
Плотность вероятности со статистикой распределения *
Диагональная матрица, на диагонали которой находятся элементы вектора
А — квадратная матрица
Собственные значения матрицы
А — квадратная матрица
А. — собственное значение
Собственный вектор матрицы, соответствующий заданному собственному значению
А — квадратная матрица
Собственные векторы матрицы
Обратная функция ошибок
Возвращает строку S как сообщение об ошибке
Экспонента в степени z
x,y — векторы данных
g — вектор начальных значений а,Ь,с
Вектор прямого преобразования Фурье (в разных нормировках)
Функция Бесселя второго рода нулевого, первого и m-го порядка
n — порядок х — аргумент
Сферическая функция Бесселя второго рода
Некоторые функции, составляющие семейства типовых функций, приведены в сокращенном виде с недостающей частью имени в виде звездочки *. Например, различные статистические функции, описывающие различные распределения, или функции вывода в файлы. Подробные сведения содержатся в разделе, на который указывает соответствующая ссылка.
MathCAD. MatLab
И другие программы этой серии
MathCAD 2001
— Арктангенса нет на панелях инструментов, поэтому его нужно найти в специальном списке функций. Вызвать этот список можно либо сочетанием [Ctrl]+[E], либо выполнив команду Insert / Function (Вставка/Функция), либо при помощи специальной кнопки панели Standard (Стандартная). В открывшемся окне есть список категорий функций (Function Category), список самих функций выбранной категории (Function Name), а также окно информации о выбранной функции. По умолчанию определена категория All (Все) и в окне Function Name находится полный список всех встроенных функций MathCAD.
Очевидно, что арктангенс нужно искать в категории Trigonometric (Тригонометрические). Среди множества всевозможных тригонометрических функций находится 2 вида арктангенса (Atan и Atan2).
Для того чтобы определить, какой из них следует выбрать, прочитаем описание для каждого:
Atan(Z). \»Returns the angle (in radians) whose tangent is z. Principal value for complex z.\» \»Возвращает угол (в радианах), для которого тангенс — это Z. Главное значение для комплексного Z\».
Atan2(x,y). \»Returns the angle (in radians) from the x-axis to a line containing the origin (0, 0) and the point (x, y). Both x and y must be real.\» \» Возвращает угол (в радианах) между осью x и линией, содержащей точку начала координат и точку (x,y). X и Y должны быть действительными\».
Очевидно, нужно использовать первую функцию. Выбираем ее и нажимаем Ok.
2) Выражение введено, но параметры его вида, установленные по умолчанию, зачастую могут не удовлетворить пользователя. Для того чтобы отредактировать вид выражения, нужно при помощи команды Format/Equation (Формат/Уравнение) вызвать соответствующее меню.
Здесь вы можете определить цвет шрифта формул (Default equation color), выбрать стиль (Style name). При помощи кнопки Modify (Модифицировать) вы можете изменить стиль текста формул: выбрать тип, размер, начертание шрифта. Чтобы поменять параметры самой математической области, выполните правый щелчок мышью по любой точке редактируемой формулы и в открывшемся контекстном меню выберите пункт Properties (Свойства).
Научная электронная библиотека
Левинсон Л М, Габдрахманова К Ф, Зиганшин С С,
1.5. Некоторые стандартные функции MathCAD
Рассмотрим некоторые стандартные функции системы MathCAD. Введем специальные обозначения для аргументов функций. Пусть первый символ имени аргумента обозначает его тип:
M – квадратная матрица;
V – вектор (матрица из одного столбца);
A – произвольная матрица;
S – симметричная матрица;
G – произвольная матрица или число;
X – вектор или число;
Z – комплексная матрица или число;
z – комплексное число;
прочие символы – скалярные величины.
Экспоненциальные и логарифмические функции
exp(X) – экспонента от X;
ln(X) – натуральный логарифм от X;
log(X) – десятичный логарифм от X;
log(X,b) – логарифм от X по основанию b.
Гиперболические и тригонометрические (прямые и обратные) функции
sin(X), cos(X), tan(X), cot(X), sec(X), csc(X) – соответственно синус, косинус, тангенс, котангенс, секанс, косеканс от X, причем аргументы указываются в радианах;
sinh(X), cosh(X), tanh(X), coth(X), sech(X), csch(X) – аналогичные гиперболические функции;
asin(z), acos(z), atan(z), acot(z), asec(z), acsc(z) – соответственно арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс от z.
Функции для работы с комплексными числами
Re(Z), Im(Z) – соответственно вещественная и мнимая части комплексного числа Z;
arg(z) – аргумент комплексного числа z (в радианах).
length(V) – возвращает число элементов вектора V;
cols(A) – возвращает число столбцов матрицы A;
rows(A) – возвращает число строк матрицы A;
matrix(m, n, f) – матрица размером mxn, значения элементов матрицы определяются f – функцией f (i, j) от двух переменных (номера строки и номера столбца). Эта функция должна быть предварительно определена пользователем;
identity(n) – единичная матрица n×n;
tr(M) – след матрицы M (сумма элементов главной диагонали);
rank(A) – ранг матрицы M;
norme(M) – эвклидова норма матрицы M, то есть корень квадратный из суммы квадратов всех элементов;
eigenvals(M) – вектор, элементы которого являются собственными числами матрицы M;
eigenvecs(M) – матрица, состоящая из нормализованных собственных векторов матрицы M;
cholesky(S) – возвращает нижнетреугольную матрицу L – результат разложения Холецкого вида L∙LT = S;
lu(M) – возвращает матрицу размера n×3n, состоящую из трех соединенных матриц P, L, U, являющихся результатом LU-разложения вида P∙M = L∙U.
Пример вычислений с матричными функциями: нахождение собственного числа путем решения матричного уравнения det(M – λE) = 0 и с помощью функции eigenvals.
Элементы статистического анализа данных
gmean(G1,G2,G3…) – среднее геометрическое аргументов;
mean(G1,G2,G3…) – среднее арифметическое аргументов;
stdev(G1,G2,G3…) – среднеквадратичное отклонение.
fft(V1), ifft(V2) – прямое и обратное быстрые преобразования Фурье над вещественными данными. V1 – вектор из 2m элементов, V2 – вектор из 1 + 2m–1 элементов, m > 2;
cfft(A), icfft(A) – прямое и обратное преобразования Фурье над вещественными и комплексными векторами и матрицами;
wave(V), iwave(V) – прямое и обратное вейвлет-преобразования, V – вектор из 2m элементов, m – целое число.
Аппроксимация, интерполяция и экстраполяция
Аппроксимация – поиск функции, которая с заданной степенью точности описывает исходные данные.
Интерполяция – определение наиболее правдоподобных промежуточных значений в интервале между известными значениями (подбор гладкой кривой, проходящей через заданные точки или максимально близко к ним).
Экстраполяция – определение наиболее правдоподобных последующих значений на основании анализа предыдущих значений (предсказание дальнейшего поведения неизвестной функции).
Применяются следующие функции MathCAD:
interp(VS,VX,VY,x) – возвращает интерполированное значение неизвестной функции при значении аргумента x. VS – вектор значений, который вернула функция regress. VX,VY – те же данные, что и для regress. Функции interp и regress используются в паре;
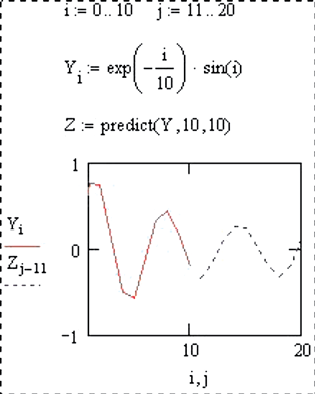
predict(V,m,n) – возвращает вектор из n предсказанных значений на основании анализа m предыдущих значений из вектора V. Предполагается, что значения функции в векторе V были получены при значениях аргумента, взятых последовательно, с одинаковым шагом. Используется алгоритм линейной предикции. Наиболее целесообразно использовать predict для предсказания значений по данным, в которых отмечены колебания.
Для интерполяции система MathCAD использует подход, основанный на применении метода наименьших квадратов.
Примеры интерполяции и экстраполяции:
1.5.1. Пусть заданы координаты пяти точек (1; 1), (2; 2), (3; 3), (4; 2), (5; 3), представляющих результаты измерения значений некоторой неизвестной функции при различных значениях x. Необходимо подобрать интерполирующую функцию (гладкую кривую), проходящую через заданные точки.
1.5.2. Дана функция y(i) = e–i/10∙sin (i). Известны значения данной функции при i = 0, 1, …, 10. Основываясь на десяти последних значениях, необходимо предсказать последующие десять значений.
Решения показаны на рис. 19.
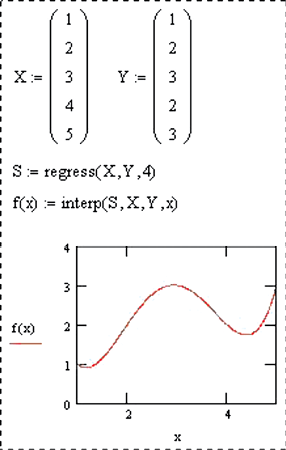
Рис. 19. Решения в MathCAD первой (а) и второй (б) задач
Нахождение корней полинома
max(G1,G2,…) – максимальное значение среди аргументов;
min(G1,G2,…) – минимальное значение среди аргументов;
if(a,b,c) – возвращает b, если a ≠ 0, иначе возвращает c;
sign(a) – возвращает –1, 0 или 1 в зависимости от знака числа a.
На рис. 20 показан пример применения функции if.
Как пишется котангенс в маткаде
Смотрите определение. Котангенс определяется как отношение косинуса к синусу, или равносильное ctg(x) = 1/tg(x).
| MEHT |       
Вот тут, признаться, не понял в чём состоит вопрос. Перевести радианы в градусы (и наоборот) можно и без инж. калькулятора, достаточно помнить, что полный оборот, соотвествующий углу в 360° будет углом 2π в радианах, следовательно углу в x° будет отвечать угол в (x/360)·2π = x·π/180 (радиан). |
| Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 24 мая 2011 0:58 | IP |
| Stanislav60 |
| Всего сообщений: 4 | Присоединился: май 2011 | Отправлено: 24 мая 2011 16:06 | IP |
| MEHT |       
Отсюда же следует что, например, углу в y (радиан) будет соответствовать градусная мера y·180°/π. Дробную часть градусов следует перевести в минуты и секунды. Полная выкладка: Аналогично находятся градусные меры остальных углов.
это за число и что с ним делать непонятно? По калькулятору sin⁻¹ (0.5) = 30° градусам, а sin(30) = 0,5. По компьютеру это выглядит следующим образом. sin(0.5) = 0.479 Что касается калькулятора, то как и у большинства инж.калькуляторов, у него, по всей видимости, имеется переключатель «градусы-радианы-грады» и выставлен он в положение «градусы». |
| Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 25 мая 2011 21:12 | IP |
| noknok |       Помогите решить задачи по алгебре срочо. Помогите решить задачи по алгебре срочо. №2 сравнить На двух станках отштамповали 1800 деталей за 12ч.Известно,что 180 деталей на первом станке штампуют на 1ч быстрее,чем на втором.Сколько деталей в час штампуют на первом станке |        sin(0.5) = 0.479 Теперь вы знаете какие однокоренные слова подходят к слову Как пишется котангенс в маткаде, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову "Как пишется котангенс в маткаде", предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором. |