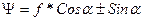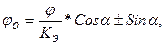КОЭФФИЦИЕНТ СОПРОТИВЛЕНИЯ ДВИЖЕНИЮ
В общем случае коэффициентом сопротивления движению тела по опорной поверхности называется отношение сил, препятствующих этому движению, к весу тела. Следовательно, коэффициент сопротивления движению позволяет учесть потери энергии при перемещении тела на данном участке.
В зависимости от природы действующих сил в экспертной практике пользуются различными понятиями коэффициента сопротивления движению.
Коэффициентом сопротивления качению — ƒ называют отношение силы сопротивления движению при свободном качении транспортного средства в горизонтальной плоскости к его весу.
На величину коэффициента ƒ, помимо типа и состояния дорожного покрытия, оказывает влияние целый ряд других факторов (например, давление в шинах, рисунок протектора, конструкция подвески, скорость и др.), поэтому более точное значение коэффициента ƒ может быть определено в каждом случае экспериментальным путем.
Потеря энергии при перемещении по поверхности дороги различных объектов, отброшенных при столкновении (наезде), определяется коэффициентом сопротивления движению ƒg. Зная величину этого коэффициента и расстояние, на которое переместилось тело по поверхности дороги, можно установить его первоначальную скорость, после чего во многих случаях.
Значение коэффициента ƒ можно приближенно определить по таблице 3[5].
| Дорожное покрытие | Коэффициент, ƒ |
| Цемент и асфальтобетон в хорошем состоянии | 0,014—0,018 |
| Цемент и асфальтобетон в удовлетворительном состоянии | 0,018—0,022 |
| Щебенка, гравий с обработкой вяжущими материалами, в хорошем состоянии | 0,020—0,025 |
| Щебенка, гравий без обработки, с небольшими выбоинами | 0,030—0,040 |
| Брусчатка | 0,020—0,025 |
| Булыжник | 0,035—0,045 |
| Грунт плотный, ровный, сухой | 0,030—0,060 |
| Грунт неровный и грязный | 0,050—0,100 |
| Песок влажный | 0,080—0,100 |
| Песок сухой | 0,150—0,300 |
| Лед | 0,018—0,020 |
| Снежная дорога | 0,025—0,030 |
Как правило, при перемещении отброшенных при столкновении (наезде) объектов движение их тормозится неровностями дороги, острые кромки их врезаются в поверхность покрытия и т.п. Учесть влияние всех этих факторов на величину силы сопротивления движению конкретного объекта не представляется возможным, поэтому значение коэффициента сопротивления движению ƒg может быть найдено лишь экспериментальным путем.
Следует помнить, что при падении тела с высоты в момент удара гасится часть кинетической энергии поступательного движения за счет прижатия тела к поверхности дороги вертикальной составляющей сил инерции. Поскольку потерянную при этом кинетическую энергию учесть не удается, нельзя определить и действительное значение скорости тела в момент падения, можно определить лишь нижний ее предел.
Отношение силы сопротивления движению к весу транспортного средства при свободном качении его на участке с продольным уклоном дороги называется коэффициентом суммарного сопротивления дороги ψ. Величина его может быть определена по формуле:
| где: | f | — | коэффициент сопротивления качению; |
| α | — | угол уклона дороги. |
Знак (+) берется при движении транспортного средства на подъем, знак (—) — при движении на спуске.
При перемещении по наклонному участку дороги заторможенного транспортного средства коэффициент суммарного сопротивления движению выражается аналогичной формулой:
| где | φ | — | коэффициент сцепления шин с поверхностью дороги; |
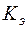 | — | коэффициент эффективности торможения транспортного средства/ |
ВРЕМЯ РЕАКЦИИ ВОДИТЕЛЯ
Под временем реакции водителя в психологической практике понимается промежуток времени с момента поступления к водителю сигнала об опасности до начала воздействия водителя на органы управления транспортного средства (педаль тормоза, рулевое колесо).
В экспертной практике под этим термином принято понимать промежуток времени t1, достаточный для того, чтобы любой водитель (психофизические возможности которого отвечают профессиональным требованиям) после того, как возникнет объективная возможность обнаружить опасность, успевал воздействовать на органы управления транспортного средства.
Очевидно между этими двумя понятиями имеется существенная разница.
Во-первых, не всегда сигнал об опасности совпадает с моментом, когда возникает объективная возможность обнаружить препятствие. В момент появления препятствия водитель может выполнять другие функции, отвлекающие его на какое-то время от наблюдения в направлении возникшего препятствия (например, наблюдение за показаниями контрольных приборов, поведением пассажиров, объектами, расположенными в стороне от направления движения, и т. п.).
Следовательно, время реакции (в том смысле, какой вкладывается в этот термин в экспертной практике) включает в себя время, прошедшее с момента, когда водитель имел объективную возможность обнаружить препятствие, до момента, когда он фактически его обнаружил, и собственно время реакции с момента поступления к водителю сигнала об опасности.
Во-вторых, время реакции водителя t1, которое принимается в расчетах экспертов, для данной дорожной обстановки величина постоянная, одинаковая для всех водителей. Она может значительно превышать фактическое время реакции водителя в конкретном случае дорожно-транспортного происшествия, однако фактическое время реакции водителя не должно быть больше этой величины, так как тогда его действия следует оценивать как несвоевременные. Фактическое время реакции водителя в течении короткого отрезка времени может меняться в широких пределах в зависимости от целого ряда случайных обстоятельств.
Следовательно, время реакции водителя t1, которое принимается в экспертных расчетах, по существу является нормативным, как бы устанавливающим необходимую степень внимательности водителя.
Если водитель реагирует на сигнал медленнее, чем другие водители, следовательно, он должен быть более внимательным при управлении транспортным средством, чтобы уложиться в этот норматив.
Было бы правильнее, по нашему мнению, назвать величину t1 не временем реакции водителя, а нормативным временем запаздывания действий водителя, такое название точнее отражает сущность этой величины. Однако поскольку термин «время реакции водителя» прочно укоренился в экспертной и следственной практике, мы сохраняем его и в настоящей работе.
Так как необходимая степень внимательности водителя и возможность обнаружения им препятствия в различной дорожной обстановке неодинаковы, нормативное время реакции целесообразно дифференцировать. Чтобы сделать это, необходимы сложные эксперименты с целью выявления зависимости времени реакции водителей от различных обстоятельств.
В экспертной практике в настоящее время рекомендуется принимать нормативное время реакции водителя t1 равным 0,8 сек. Исключение составляют следующие случаи.
Если водитель предупрежден о возможности возникновения опасности и о месте предполагаемого появления препятствия (например, при объезде автобуса, из которого выходят пассажиры, или при проезде с малым интервалом мимо пешехода), ему не требуется дополнительное время на обнаружение препятствия и принятие решения, он должен быть подготовлен к немедленному торможению в момент начала опасных действий пешехода. В подобных случаях нормативное время реакции t1 рекомендуется принимать 0,4—0,6 сек (большее значение — в условиях ограниченной видимости).
Когда водитель обнаруживает неисправность органов управления лишь в момент возникновения опасной обстановки, время реакции, естественно, возрастает, так как при этом необходимо дополнительное время для принятия водителем нового решения, t1 в этом случае равно 2 сек.
Правилами движения водителю запрещается управлять транспортным средством даже в состоянии самого легкого алкогольного опьянения, а также при такой степени утомления, которая может повлиять на безопасность движения. Поэтому влияние алкогольного опьянения на t1 не учитывается, а при оценке степени утомляемости водителя и его влияния на безопасность движения следователь (суд) учитывает обстоятельства, которые вынудили водителя управлять транспортным средством в подобном состоянии.
Полагаем, что эксперт в примечании к заключению может указать на возрастание t1 в результате переутомления (после 16 час работы за рулем примерно на 0,4 сек).
Определение силы сопротивления в физике и её формула
Что такое сила сопротивления в физике
Сила сопротивления — сила, которая возникает во время движения тела в жидкой или газообразной среде и препятствует этому движению.
Важно уметь отличать силу сопротивления от силы трения. Во втором случае рассматривается характер взаимодействия твердых тел друг с другом. Таким образом, трение можно наблюдать, когда какой-либо предмет перемещается по поверхности другого. Вектор этой силы будет направлен в противоположную сторону направления движения.
Для того чтобы рассчитать силу сопротивления необходимо умножить коэффициент сопротивления материала на силу, провоцирующую перемещение этого предмета.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В качестве примера силы сопротивления можно рассмотреть движение поезда. Воздух, окружающий состав, замедляет скорость его перемещения, то есть возникает сила сопротивления.
От чего зависит в механике и динамике
Сила сопротивления зависит от нескольких факторов. На ее величину оказывают влияния следующие характеристики:
Энергию создают внешние силы за счет своей работы с мощностью по определению силы сопротивления. Откуда, A=K. Таким образом,
В этом случае зависимость силы сопротивления от скорости перемещения объекта возрастает и становится пропорциональна ее второй степени. В отличие от силы внутреннего трения ее обозначают, как силу динамического лобового сопротивления.
Следует отметить, что теория, в которой частицы среды полностью увлекаются транспортируемыми телами, преувеличена. В условиях реального времени любой движущийся предмет обтекаем потоком, который снижает воздействие на него сил сопротивления. Поэтому при расчетах нередко используют коэффициент сопротивления С, обозначая силу лобового сопротивления формулой:
Разновидности сил сопротивления
Существует несколько типов силы сопротивления, отличающихся по характеру воздействия на движущиеся предметы.
Сила сопротивления качению
Сила сопротивления качению обозначается, как Pf. В данном случае сила определяется несколькими факторами:
Состояние и тип опорной поверхности определяет величину коэффициента сопротивления качению, который обозначается f. Если в среде повышается температура, и возрастает давление, то данный показатель будет уменьшаться.
Сила сопротивления воздуха
Сила сопротивления воздуха или величина лобового столкновения Pв образуется в результате различных показателей давления. Данная характеристика напрямую зависит от интенсивности вихреобразования спереди и сзади движущегося предмета. Указанные параметры определяются формой перемещающегося тела.
Большее влияние на силу сопротивления будет оказывать вихреобразование в передней части объекта. Если плоскостенную фигуру закруглить спереди и сзади, то получится снизить сопротивление до 72%.
Рассчитать силу лобового сопротивления можно по формуле:
сх — обтекаемость или коэффициент лобового сопротивления; p — плотность воздуха; Fв — площадь лобового сопротивления (миделевого сечения).
Во время поступательного движения масса объекта встречает сопротивление разгону, то есть ускорению. Найти данную силу можно с помощью второго закона Ньютона.
где m выражает массу движущегося объекта, а \(dVdt\) обозначает ускорение центра масс.
Как найти трение
Определить силу сопротивления можно, если применить третий закон Ньютона. Для того чтобы предмет равномерно перемещался по опоре в горизонтальном направлении, к нему необходимо приложить силу, соизмеримой с силой сопротивления. Корректно рассчитать данные величины можно с помощью динамометра. Сила сопротивления будет прямо пропорциональна массе объекта. Более точные расчеты производятся с учетом u коэффициента, который зависит от следующих факторов:
Рассчитывая силу сопротивления, используют постоянную величину g, равную 9,8 метров на сантиметр в квадрате. При этом если движение тела происходит на определенной высоте, на него оказывает воздействие сила трения воздуха. Данная величина зависит от скорости, с которой движется предмет. Искомая величина определяется с помощью следующей формулы только при условии, что предмет перемещается на небольшой скорости:
где V является скоростью перемещения тела, a — коэффициентом сопротивления среды.
Силы сопротивления при больших скоростях
Сила сопротивления, оказывающая воздействие на движущиеся предметы с малой скоростью, зависит от нескольких внешних факторов. К таким условиям относятся:
В условиях больших скоростей характер действия силы сопротивления несколько изменяется. Законы вязкого трения в этом случае не применяются для воздуха и воды. Если скорость предмета составляет 1 сантиметр в секунду, то данные факторы учитываются лишь тогда, когда тела обладают крошечными размерами, измеряемыми в миллиметрах.
Если пловец ныряет в воду, то на него будет действовать сила сопротивления. Однако в данном случае закон вязкого трения не будет действовать.
Объект, двигаясь с малой скоростью в водной среде, плавно обтекается жидкостью. Сила сопротивления в данном случае будет рассчитываться, как сила вязкого трения. Если скорость большая, то с задней части перемещающегося тела наблюдается более сложное движение жидкости с образованием необычных по форме фигур, вихрей, колец. Картина таких струек будет постоянно изменяться. Движение такого характера называется турбулентным. Турбулентное сопротивление все еще будет определяться скоростью и размерами тела, но не так, как при вязком сопротивлении. В данном случае сила рассчитывается пропорционально квадрату скорости и линейным размерам предмета. Вязкость водной среды более не имеет решающего значения, определяющая функция переходит к показателю плотности.
Сила турбулентного сопротивления рассчитывается по формуле:
где V обозначает показатели скорости движения, L — соответствует линейным размерам тела, p — равна плотности среды.
ДВИЖЕНИЕ В ВЯЗКОЙ СРЕДЕ. ВИДЫ СИЛ СОПРОТИВЛЕНИЯ. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ СОПРОТИВЛЕНИЯ
ДВИЖЕНИЕ В ВЯЗКОЙ СРЕДЕ. ВИДЫ СИЛ СОПРОТИВЛЕНИЯ. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ СОПРОТИВЛЕНИЯ
Волкова А.Ю. 1 *, Суетин В.П. 2
1, 2 Уральский государственный университет путей сообщения, Екатеринбург, Россия
* Корреспондирующий автор (alenavolkova98[at]yandex.ru)
Аннотация
Изучен процесс торможения вращающегося твердого тела. Выполнен модельный эксперимент, в котором трение в системе меняется с помощью парусов, ориентированных под разными углами относительно воздушного потока. Определен интервал скоростей, при которых играют роль различные виды трения: сухое, вязкое и аэродинамическое, а также вычислены основные параметры разных видов трения (момент силы сухого трения, коэффициент вязкого трения), закономерности их изменения в зависимости от условий эксперимента.
Ключевые слова: коэффициент сопротивления, вязкое трение, эксперимент
MOVEMENT IN VISCOUS MEDIA. TYPES OF RESISTANCE FORCES. DETERMINATION OF RESISTANCE COEFFICIENTS
Volkova A.Yu. 1 *, Suetin V.P. 2
1, 2 Ural State University of Railway Transport, Yekaterinburg, Russia
* Correspondent author (alenavolkova98[at]yandex.ru)
Abstract
The process of friction of a rotating solid is studied. A model experiment is performed in which friction in the system is changed using sails oriented at different angles with respect to the airflow. The speed range is determined at which various types of friction play an important role: dry, viscous and aerodynamic, and the main parameters of different types of friction (the moment of dry friction force, coefficient of viscous friction) and the laws of their change depending on the experimental conditions are calculated.
Keywords: resistance factor, viscous friction, experiment.
В процессе торможения любого движущегося тела при разных скоростях играют роли разные виды трения. При самых низких скоростях это сухое трение, когда коэффициент трения не зависит от скорости. Для более высоких скоростей трение будет вязким, когда сила трения зависит от скорости. Далее при еще более высоких скоростях трение уже будет аэродинамическим, когда сила трения пропорциональна квадрату скорости, и так далее. Для исследования видов сил сопротивления мы изучили процесс торможения вращающегося твердого тела. При этом мы определили интервал скоростей, при которых в процессе торможения основную роль играют различные силы торможения (сухое, вязкое, аэродинамическое). Для изменения вязкого и аэродинамического трения на твердое тело устанавливаем два паруса. Изменяя положение парусов относительно потока воздуха, моделируем величину коэффициентов вязкого и аэродинамического трения. Для определения вида трения и коэффициента трения исследуем зависимости угловой скорости вращения тела от времени от времени.
Зависимость угловой скорости вращения твердого тела можно найти из уравнения динамики вращательного движения [1, с. 140]:

где I – момент инерции системы, М – момент сил сопротивления.
Для сухого трения сила трения не зависит от скорости вращения, а момент силы М = –М0 = const. В этом случае из уравнения (1) находим:

Тогда угловая скорость вращения уменьшается по линейному закону в зависимости от времени.
Вязкое трение характеризуется линейной зависимостью силы трения от скорости движения (F = αv, где α – коэффициент сопротивления). Зависимость между моментом сил трения и угловой скоростью тоже будет линейной (М = –kω) [2, с. 332].
В данном случае решением уравнений (1) и (2) будут следующие зависимости:

где γ = k/I. Тогда линейная зависимость угловой скорости от угла поворота системы и зависимость логарифма скорости от времени [3, с. 48]:

Если расстояние от оси вращения до каждого из парусов равно R, то коэффициент сопротивления:

Коэффициент γ определяется методом наименьших квадратов по зависимости lnω от времени[4, с. 105].
Для изучения видов сил сопротивления и определения коэффициентов сопротивления собираем схему экспериментальной установки, которая состоит из вращающегося столика, стержня и двух парусов (см. рисунок 1).
Рис. 1 – Схема экспериментальной установки
Наша установка позволяет определять период вращения от начала вращения вплоть до остановки тела. Для определения средней угловой скорости вращения при прохождении n-ого оборота воспользуемся ее определением
[5, с. 13]:

Так как угловая скорость является переменной величиной, то полученное ее значение является средним значением угловой скорости за n-й период вращения [6, с. 113].
Определение видов сил сопротивления и определение коэффициентов сопротивления
На рис. 2 представлен экспериментальный график зависимости угловой скорости вращения столика от времени для ориентации парусов вдоль потока (φ=0 0 ).
Рис. 2 – График зависимости угловой скорости вращения столика от времени для угла ориентации парусов
вдоль воздушного потока (φ=0 0 )
Рис. 3 – График зависимости логарифма угловой скорости вращения столика от времени
для угла ориентации парусов 0 0
Таким образом, с помощью метода наименьших квадратов по зависимости угловой скорости вращения столика от времени, мы определили отношение момента силы трения к моменту инерции для сухого трения.
Вычислили момент силы сухого трения Мтр по формуле [7, с. 61]:

где β – это отношение момента силы трения к моменту инерции для сухого трения, а I – момент инерции системы, который определяется отдельно. Момент силы сухого трения слабо зависит от угла ориентации парусов [8, с. 132]. Среднее его значение указано в Таблице 1.
Также с помощью метода наименьших квадратов по зависимости логарифма угловой скорости вращения столика от времени для вязкого трения, мы определили коэффициент γ.
После чего вычислили коэффициент вязкого трения по формуле [9, с. 29]:

где γ – коэффициент, определенный с помощью метода наименьших квадратов по зависимости логарифма угловой скорости вращения столика от времени для вязкого трения, R – расстояние от оси вращения до каждого из парусов (R = 0,13 м) [10, с. 31]. Результаты измерений и вычислений момента силы сухого трения и коэффициента вязкого трения заносим в Таблицу 1.
Таблица 1 – Результаты измерений и вычислений момента силы сухого трения и коэффициента вязкого трения
от угла ориентации парусов относительно воздушного потока
| Угол ориентации парусов φ, град. кг/с | ||||
| 0 | 0,14 | 0,001 | 0,0362 | 0,007358 |
| 30 | 0,0912 | 0,018537 | ||
| 60 | 0,1152 | 0,023415 | ||
| 90 | 0,1413 | 0,02872 |
По полученным результатам для коэффициента вязкого трения построим график зависимости коэффициента вязкого трения от угла поворота парусов (см. рис. 4).
Рис. 4 – Зависимость коэффициента вязкого трения от угла ориентации парусов
График зависимости коэффициента вязкого трения от угла поворота парусов нелинейный. При изменении угла поворота парусов относительно воздушного потока коэффициент вязкого трения увеличивается в 4 раза.
Данное исследование иллюстрирует экспериментальное доказательство существования различных видов трения, позволяет определить их границы по величине скорости вращения, а также позволяет определить важнейшие параметры сил трения и их зависимость от внешних условий эксперимента.
| Конфликт интересов | Conflict of Interest |
| Не указан. | None declared. |
Список литературы / References
Список литературы на английском языке / References in English