Математика для блондинок
Страницы
среда, 25 января 2012 г.
Экспонента на калькуляторе
Что такое экспонента и с чем её едят, мы разберемся в следующий раз. Сейчас мы разберемся, как где находится экспонента на калькуляторе и как её на калькуляторе считать. Нажимайте на ссылку, калькулятор откроется в новом окне. Приступим к практическим занятиям. Нажимайте на те же кнопочки, что нажимал я и смотрите на результат.
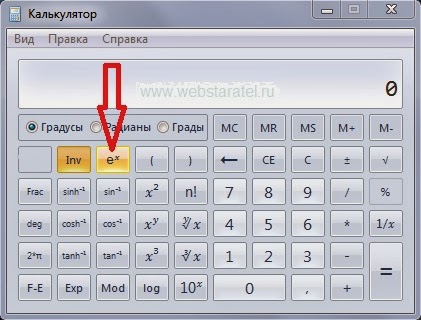
Для начала возведем число е в степень 4. В начале нужно набрать показатель степени. Нажимаем на кнопочку 4. Результат нашего вмешательства в беззаботную жизнь калькулятора можете посмотреть на картинке.
После этого нажимаем на специальную кнопочку экспоненты, обозначенную на калькуляторе е в степени х. Как видно из рисунка, калькулятор нас правильно понял и отреагировал именно так, как нам нужно.
Для вычисления заданного нами примера экспоненты необходимо нажать кнопочку равно.
Всё, мы получили требуемое значение.
Для начала вычислим е в первой степени. Собственно, это и будет значение числа е. Напомню, что любое число в первой степени равно самому себе. Порядок нажимания кнопочек пронумерован на картинке красными цифрами.
Мы получили округленное до 14 знаков после запятой значение числа е:
е 1 =е=2,71828182845905≈2,718
Число е подчиняется всем свойствам степени, как и любое другое число. Результаты возведения его в степень такие же, как у чисел больших единицы. При возведении в степень больше единицы результат будет больше первоначального. Для примера, возведем число е в не целую степень 9,876. Порядок нажимания кнопочек показан красными цифрами, результат виден на картинке.
Если показатель степени меньше единицы но больше нуля, то результат получится меньше первоначального но больше единицы. Это соответствует извлечению корня из числа е. Если на калькуляторе ввести показатель степени 0,5 (что равнозначно 1/2) то мы найдем квадратный корень числа е. Мы для примера возьмем экспоненту в степени 0,123
По логике, дальше следует показатель степени 0. Число е, как и любое другое число в нулевой степени, равняется единице. Это мы знаем и без калькулятора.
Мы получили число, обратное числу е:
Дальше пробуем добыть экспоненту со степенью меньше минус единицы.
Здесь полученный результат нужно преобразовать в удобоваримый для математиков вид. Делается это так:
Если после полученного на калькуляторе результата нажать ещё раз на знак равенства, десятичная дробь преобразуется в обычную дробь. Результат этой хитрой операции виден на картинке.
Но этот результат мне не нравится. Одна тысячная почти в два раза больше пяти десятитысячных. Если бы программа с калькулятором была русской, я бы подумал, что эту функцию писал бывший госслужащий, привыкший всё увеличивать в два раза (нужно же откуда-то себе воровать). Остается только предупредить, что и калькулятору полностью доверять нельзя, нужно самому анализировать результат, который он выдает.
В заключение найдем экспоненту с показателем степени больше минус единицы, но меньше нуля.
Теперь попробуем преобразовать результат в обычную дробь.
На этот раз калькулятор выдал более красивый результат. Но я уже ему не верю. Проверим результат преобразования, разделив на калькуляторе числитель на знаменатель. Результат деления записан ниже экспоненты.
Вот теперь можно поверить калькулятору, поскольку погрешность преобразования совсем незначительная. Округление даже до пяти знаков после запятой дает одинаковый результат.
Что делать, если вы пользуетесь виндосовским калькулятором и даже в инженерном варианте нет заветной кнопочки «е в степени икс»? Найдите кнопочку «Inv», рядом с ней есть кнопочка натурального логарифма «ln». Смело нажимайте кнопочку «Inv».
 |
| Экспонента на калькуляторе Виндовс картинка 1 |
После нажатия этой кнопочки, расположенная рядом кнопочка натурального логарифма волшебным образом превратится в кнопочку «число е в степени икс».
 |
| Экспонента на калькуляторе Виндовс картинка 2 |
По замыслу создателей калькулятора, такие превращения натурального логарифма и ежу понятны. Но.
Во-первых. Ёжик должен быть трезвым.
Во-вторых. Ёжик должен быть сообразительным.
В третьих. В памяти ежа на первом месте должны бить свойства натуральных логарифмов, а не какая-то ерунда типа любви, смысла жизни или завтрашнего урока по математике.
Что такое экспонента (exp) на калькуляторе?
Редкий случай, когда известный математик Rafail ошибся.
Кнопка exp означает ввод числа в нормальном виде, то есть мантисса и порядок.
Сначала вы вводите мантиссу, то есть значащие цифры, потом нажимаете exp и вводите порядок числа.
Например, вам надо ввести число 50 миллионов 50 000 000. Можно так и ввести, но проще нажать 5 exp 7.
На экране вы увидите 5Е7, что равно
5*10^7=50 000 000. Те же 50 миллионов.
Функция экспонента exp(x) означает, что в степень (х) нужно возвести число е (основание натуральных логарифмов). Таким образом exp(x)=е^x.
На дисплее инженерного калькулятора экспонента отображается значком «E» и если ввести затем например после Е число 5, то математический ответ будет равен 10 в степени введенного числа, т. е. exp (5)=10^5=100 000; поэтому по данном вопросу можно согласиться с мнением и ответом автора Mefody66
Название планеты – ПАЛЛАДА.
Немецкого математика, механика, физика и астронома Карла Фридриха Гаусса (1777- 18550) называли «королем математиков». Он не только занимался теорией чисел, но и включал в свою научную деятельность естественные науки.
В начале XIX века немецкий астроном Кеппер высказал предположение, что между Марсом и Юпитером должна быть еще какая-то планета. Заметил ее итальянский астроном Пиацци и стал наблюдать за ней и сумел сделать несколько измерений. Однако, из-за болезни наблюдения прервались и после возобновления наблюдений планету уже найти/увидеть так и не удалось.
Гаусс, будучи еще молодым математиком, заинтересовался этим вопросом. Используя точные координаты положения планеты, полученные Пиацци, он сумел рассчитать ОРБИТУ движения неизвестной планеты. Благодаря этим расчетам в декабре 1801 года эта планета была найдена там, где должна была находиться – на одной из точек своей орбиты.
Новой планете Пиацци дал название Церера. К удивлению астрономов, на этой же орбите немецкий любитель астрономии Ольберс открыл еще одну, вторую планету, которую назвал – ПАЛЛАДА.
То есть если корень из Х равно Y, то Y в квадрате равно Х. Очевидно, что для чисел, больших единицы, Х всегда будет больше, чем Y.
В случае единицы подкоренное число равно корню: то есть корень из единицы равен единице.
В случае чисел, меньших единицы, то есть дробей, корень из числа (в отличие от чисел, больших единицы) будет уже больше подкоренного выражения. Например, √0,001=0,1.При этом 0,1>0,001.
Вот так. А что касается корня из трех, то он равен примерно 1,7 и, как видно, меньше трех.
Цифра 6, из которой и состоит наше число 66, удивительная. Если ее перевернуть вверх тормашками, то получится другая цифра, 9. То есть, если число 66 таким образом перевернуть, то получим число 99, которое ровно в полтора раза больше, чем 66.
Туманные вычисления (перевод термина fog computing)- концепция архитектуры вычислений при которой обработка данных происходит на конечных устройствах сети (разновидность распределенных вычислений), в концепции облачных вычислений обработка данных происходит в облаке
В России туманными вычислениями занимаются Минкомсвязи, Минпромторг и др.ведомства
В мире туманными вычислениями занимается организация OpenFog Consortium
Инженерный калькулятор онлайн с самыми точными расчетами!
Почему мы так решили? Наш онлайн калькулятор оперирует числами вплоть до 20 знаков после запятой, в отличие от других. Kalkpro.ru способен точно и достоверно совершить любые вычислительные операции, как простые, так и сложные.
Только корректные расчеты по всем правилам математики!
В любой момент и в любом месте под рукой, универсальный инженерный калькулятор онлайн выполнит для вас любую операцию абсолютно бесплатно, практически мгновенно, просто добавьте программу в закладки.
Всё для вашего удобства:
Содержание справки:
Комплекс операций инженерного калькулятора
Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.
Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.
Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.
Ввод цифр производится в двух вариантах:
Инструкция по функциям инженерного калькулятора
Как пользоваться MR MC M+ M- MS
Как пользоваться инженерным калькулятором – на примерах
Как возвести в степень
Чтобы возвести, к примеру, 12^3 вводите в следующей последовательности:
12 [x y ] 3 [=]
12, клавиша «икс в степени игрик» [xy], 3, знак равенства [=]
Как найти корень кубический
Допустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:
729 [3√x] [=]
729, [ 3 √x] «кубический корень из икс», равенства [=]
Как найти корень на калькуляторе
Задача: Найти квадратный корень 36.
Решение: всё просто, нажимаем так:
36 [ y √x] 2 [=]
36, [ y √x] «корень из икса, в степени игрик», нужную нам степень 2, равно [=]
При помощи этой функции вы можете найти корень в любой степени, не только квадратный.
Как возвести в квадрат
Для возведения в квадрат онлайн вычислительная программа содержит две функции:
[x y ] «икс в степени игрик», [X 2 ] «икс в квадрате»
Последовательность ввода данных такая же, как и раньше – сначала исходную величину, затем «x^2» и знак равно, либо если не квадрат, а произвольное число, необходимо нажать функцию «x^y», затем указать необходимую степень и так же нажать знак «равно».
Например: 45 [x y ] 6 [=]
Ответ: сорок пять в шестой степ. равно 8303765625
Как произвести онлайн расчет синусов и косинусов, тангенсов
Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами.
1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.
Для включения того или иного режима измерения нажмите нужную кнопку:
В качестве самого простого примера найдем синус 90 градусов. Нажмите:
90 [sin] [=]
Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:
60 [cos] [=]
Для их ввода необходимо переключить интерфейс, нажав [Inv], появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.
Преобразование с кнопкой Dms и Deg на калькуляторе
[Deg] позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. [Dms] производит обратный перевод – в формат «градусы; минуты; секунды».
Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:
35,140453 [Deg] [=] 35,23459166666666666666
Переведем в прежний формат: 35,23459166666666666666 [Dms] [=] 35,140453
Десятичный логарифм онлайн
Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:
1 [log] [=]
Получается 0 в итоге. Для подсчета lg100 нажмем так:
100 [log] [=]
Так же вычисляется натуральный логарифм, но кнопкой [ln].
Как пользоваться памятью на калькуляторе
Существующие кнопки памяти: M+, M-, MR, MS, MC.
Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.
MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.
Пример. Внесем сто сорок пять в память программы:
145 [MR]
После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:
На экране отобразится снова 145.
Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем [M+], либо [M-] для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой [MR] получится 230, а во втором, после нажатия [M-] и [MR] получится 60.
Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.
Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!
Уравнения экспоненты по математике
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Экспонента представляет собой показательную функцию \[y(x) =e^x,\] производная которой равна самой функции. Экспоненту обозначают: \[e^x, exp(x), Exp(x) \]
Экспонента обладает свойствами показательной функции с основанием степени е > 1. Основанием степени экспоненты является число «е». Это иррациональное число. Оно примерно равно:
Выражение числа «е» через предел последовательности. Число «е» можно выразить через предел последовательности. Это, так называемый, второй замечательный предел:
Выражение числа е в виде ряда
\[e = 2+1/2!+1/3!+1/3!+ \cdots +1/n!+ \cdots \]
На графике представлена экспонента, \[e\] в степени \[x:\]
На графике видно, что экспонента монотонно возрастает.
Что касается основных формул, то они такие же, как и для показательной функции с основанием степени \[е.\]
Выражение показательной функции через экспоненту:
Где можно решить уравнение с экспонентой онлайн?
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
Как пишется экспонента в калькуляторе
Send Us Your Feedback / Suggestion
For further assistance, please Contact Us
Обнаружен блокировщик рекламы
Поскольку мы изо всех сил пытались сделать для вас онлайн-расчеты, мы обращаемся к вам с просьбой предоставить нам разрешение, отключив Adblocker для этого домена.
ДОБАВИТЬ ЭТОТ КАЛЬКУЛЯТОР НА ВАШ ВЕБ-САЙТ:
Добавьте калькулятор экспоненты на свой веб-сайт, чтобы упростить использование этого калькулятора напрямую. Создайте учетную запись для этого виджета без проблем, поскольку он на 100% бесплатный, простой в использовании и вы можете добавить его на несколько онлайн-платформ.
Загрузите приложение «Калькулятор экспоненты» для мобильного телефона, чтобы вы могли рассчитать свои значения в своих руках.
Онлайн-калькулятор экспоненты, который поможет вам вычислить значение любого положительного или отрицательного целого числа в любой степени. Кроме того, этот калькулятор степени дроби показывает результаты степени дроби любого числа. Этот полезный контент будет охватывать все связанные темы, как рассчитать это вручную, и многие другие интересные данные. Но начнем с основ!
Вы также можете использовать наш онлайн-калькулятор в научном представлении, который позволяет складывать, вычитать, умножать или делить любые числа в экспоненциальном представлении.
Что такое экспонента?
В математике это показывает, сколько копий числа умножаются вместе. Например; 74, 7 – основание, а 4 – показатель степени. В этом примере 4 копии 7 умножаются, чтобы получить 2401 как 7 * 7 * 7 * 7.
Очень легко производить вычисления с небольшими значениями, но для больших и десятичных оснований или для отрицательных или десятичных больших степеней используйте наш онлайн-калькулятор экспонента в степени.
Основные правила:
Есть несколько основных правил возведения в степень:
Правило продукта:
При умножении основного члена на два разных показателя степени равнодействующей обеих степеней становится степень основания. Например
Правило частного:
При делении основного члена на два разных показателя степени разность обеих степеней равна степени основания. Например
Правило нуля:
Показатель любого числа будет равен 1. E; g
Где b – любое целое число (положительное или отрицательное).
Кроме того, вы можете попробовать наш онлайн-exp калькулятор журнала и антилогарифмический калькулятор, который является обратной функцией экспоненты.
Как вычислить экспоненты для любого целого числа (шаг за шагом):
Расчеты мощности упрощаются с помощью этого калькулятора мощности, который помогает выполнять вычисления для всех целых чисел (отрицательных, положительных, дробных). Впереди ручной пример:
Пример:
Найти 3 в степени 7?
Решение:
Здесь x равно 3, а n равно 7. Итак,
\ ((3) ^ 7 = 3 * 3 * 3 * 3 * 3 * 3 * 3 \)
Кроме того, если у вас есть отрицательные или дробные основания или экспонента в степени, попробуйте наш онлайн-калькулятор отрицательных показателей, который поможет вам быстро определить результаты отрицательных или дробных входов.
Как использовать онлайн-калькулятор экспоненты:
Просто следуйте приведенным ниже инструкциям для получения точных результатов.
Входы:
Выходы:
Как только вы введете все обозначенные поля, калькулятор покажет:
Конечное примечание:
Теперь вычисление показателей для отрицательных и положительных целых чисел стало очень простым с помощью этого калькулятор экспоненты показателей. Этот инструмент лучше всего подходит как для студентов, так и для профессионалов.