Как извлечь корень в Python (sqrt)
Но обо всём по порядку.
Что такое квадратный корень
Корнем квадратным из числа «X» называется такое число «Y», которое при возведении его во вторую степень даст в результате то самое число «X».
Операция нахождения числа «Y» называется извлечением квадратного корня из «X». В математике для её записи применяют знак радикала:
Нотация питона отличается в обоих случаях, и возведение в степень записывается при помощи оператора » ** «:
a = 2 b = a ** 2 print(b) > 4
import math import random # пример использования функции sqrt() # отыщем корень случайного числа и выведем его на экран rand_num = random.randint(1, 100) sqrt_rand_num = math.sqrt(rand_num) print(‘Случайное число = ‘, rand_num) > Случайное число = 49 print(‘Корень = ‘, sqrt_rand_num) > Корень = 7.0
Квадратный корень
Положительное число
import math print(math.sqrt(100)) > 10.0
А можете — из вещественных:
import math print(math.sqrt(111.5)) > 10.559356040971437
Легко проверить корректность полученных результатов с помощью обратной операции возведения в степень:
print(math.sqrt(70.5)) > 8.396427811873332 # возвести в степень можно так print(8.396427811873332 ** 2) > 70.5 # а можно с помощью функции pow() print(pow(8.396427811873332, 2)) > 70.5
Отрицательное число
Функция sqrt() не принимает отрицательных аргументов. Только положительные целые числа, вещественные числа и ноль.
Такая работа функции идёт вразрез с математическим определением. В математике корень спокойно извлекается из чисел меньше 0. Вот только результат получается комплексным, а таким он нужен для относительно узкого круга реальных задач, вроде расчетов в сфере электроэнергетики или физики волновых явлений.
print(math.sqrt(-1)) > ValueError: math domain error
Функция sqrt() корректно отрабатывает с нулём на входе. Результат тривиален и ожидаем:
Кубический корень
Само название функции sqrt() намекает нам на то, что она не подходит для извлечения корня степени отличной от двойки. Поэтому для извлечения кубических корней, сначала необходимо вспомнить связь между степенями и корнями, которую продемонстрируем на корне квадратном:
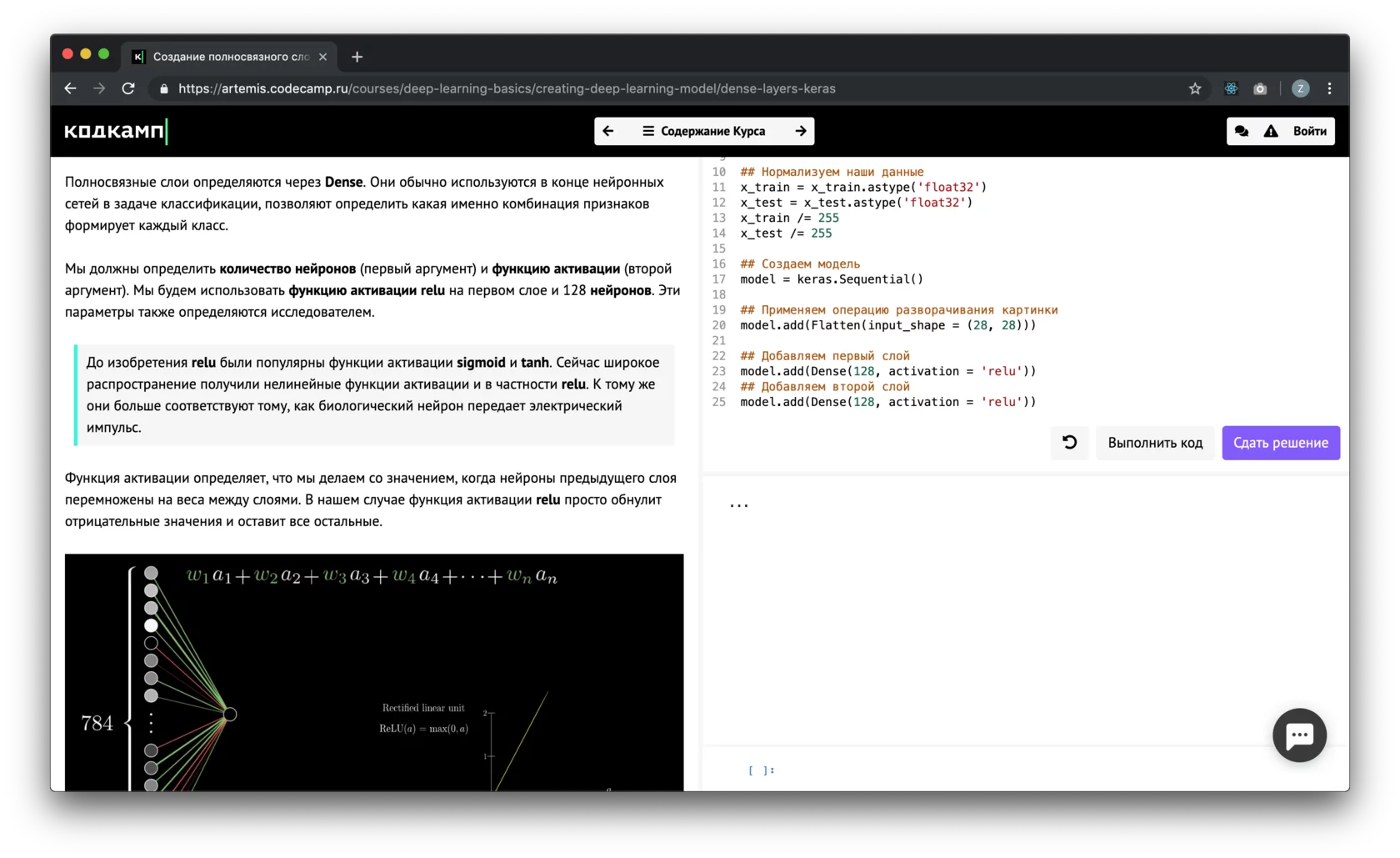
# Квадратный корень можно извлечь с помощью операции возведения в степень «**» a = 4 b = a ** 0.5 print(b) > 2.0
? Таким образом, извлечь кубический корень в Python можно следующим образом:
Корень n-степени
То, что справедливо для корня третьей степени, справедливо и для корней произвольной степени.
# извлечём корень 17-й степени из числа 5600 x = 5600 y = 17 z = pow(x, (1/y)) print(z) > 1.6614284717080507 # проверяем корректность результата print(pow(z, y)) > 5600.0
Но раз уж мы разбираемся с математической темой, то попытаемся мыслить более обобщённо. С помощью генератора случайных чисел с заданной точностью будем вычислять корень случайной степени из случайного числа:
import random # точность можно задать на ваше усмотрение x = random.randint(1, 10000) y = random.randint(1, 100) z = pow(x, (1 / y)) print(‘Корень степени’, y, ‘из числа’, x, ‘равен’, z) # при проверке вероятны незначительные расхождения из-за погрешности вычислений print(‘Проверка’, pow(z, y)) # но специально для вас автор накликал целочисленный результат > Корень степени 17 из числа 6620 равен 1.6778624404513571 > Проверка 6620.0
Решение реальной задачи с использованием sqrt
Корень — дитя геометрии. Когда Пифагор доказал свою знаменитую теорему, людям тут же захотелось вычислять стороны треугольников, проверять прямоту внешних углов и сооружать лестницы нужной длины.
Соотношение a2 + b2 = c2, где «a» и «b» — катеты, а «c» — гипотенуза — естественным образом требует извлекать корни при поиске неизвестной стороны. Python-а под рукой у древних греков и вавилонян не было, поэтому считать приходилось методом приближений. Жизнь стала проще, но расчет теоремы Пифагора никто не отменял и в XXI веке.
? Решим задачку про вышку сотовой связи. Заказчик требует рассчитать высоту сооружения, чтобы радиус покрытия был 23 километра. Мы неспешно отходим на заданное расстояние от предполагаемого места строительства и задумчиво смотрим под ноги. В голове появляются очертания треугольника с вершинами:
Модель готова, приступаем к написанию кода:
Расчёт выполнен, результат заказчику предоставлен. Можно идти пить чай и радоваться тому, что теперь ещё больше людей смогут звонить родным и сидеть в интернете.
Извлечение корней в Python
Под извлечением корня из какого-либо числа чаще всего подразумевают нахождение решение уравнения x в степени n = value, соответственно для квадратного корня, число n — это два, для кубического — 3. Чаще всего под результатом и числом подразумеваются вещественные числа.
В программировании нахождение корней используется очень часто. Разберемся, как и какими методами можно эффективно извлекать корни из числа. Вначале рассмотрим, какие способы есть в Python, и определим самый эффективный. Потом более подробно разберём, как можно найти не только квадратный корень из числа, но и кубический, и потом корень n степени.
Способы извлечения корня
В языке программирования Python 3 существует три способа извлечения корней:
Если же нам нужно вычислить в Python корень квадратный из суммы квадратов, то можно воспользоваться функцией hypot из модуля math. Берется сумма квадратов аргументов функции, из нее получается корень. Аргументов у функции два.
Еще одним, чуть более универсальным методом, будет использование возведения в степень. Известно, что для того, чтобы взять корень n из числа, необходимо возвести его в степень 1/n. Соответственно, извлечение квадратного корня из числа 4 будет выглядеть так:
Последний метод использует функцию pow(value, n). Эта функция в качестве аргумента value возьмет число, которое необходимо возвести в степень, а второй аргумент будет отвечать за степень числа. Как и в предыдущем методе, необходимо использовать дробь, для того, чтобы получить корень числа.
Какой метод быстрее?
Для того, чтобы определить какой же метод предпочтительнее использовать, напишем программу. Замерять время выполнения будем с помощью метода monotonic библиотеки time.
Как видно, самое быстрое решение — использовать **. На втором месте метод sqrt, а pow — самый медленный. Правда, метод sqrt наиболее нагляден при вычислении в Python квадратных корней.
Квадратный корень
Для извлечения квадратного корня самым наглядным способом, правда не самым быстрым, будет использование sqrt из модуля math.
Но можно использовать и трюки с возведением в степень 1/2, что тоже будет приводить к нужному результату.
Кубический корень
Для извлечения кубического корня в Python 3 метод sqrt не подойдет, поэтому воспользуйтесь возведением в степень 1/3:
Корень n-степени
Корень n-степени из числа в Python извлекается можно получить двумя способами с помощью возведения в степень 1.0/n:
Как было проверено выше, оператор ** быстрее. Поэтому его использовать более целесообразно. Приведем пример вычисления кубических корней в Python 3 с помощью этих двух методов:
Корень отрицательного числа
Рассмотрим, как поведут себя функции, если будем брать корень из отрицательного числа.
Как видим, функция sqrt выдаёт исключение.
Теперь посмотрим, что будет при использовании других методов.
Как видно из результата, оператор ** не выдает исключения и возвращает некорректный результат. Функция pow работает корректно. В результате получаем комплексное число 2j, что является верным.
Вывод
В Python существуют два универсальных способа для извлечения корня из числа. Это возведение в необходимую степень 1/n. Кроме того, можно воспользоваться функцией из математического модуля языка, если необходимо извлечь квадратный корень числа.
Все эти методы имеют свои преимущества и недостатки. Самый наглядный это sqrt, но подходит только для квадратный корней из числа. Остальные методы не такие элегантные, но легко могут извлечь корень нужной степени из числа. Кроме того оператор ** оказался наиболее быстрым при тестировании.
Необходимо также помнить про целочисленное деление, неправильное использование которого может приводить к ошибке в вычислении.
Степень в Python — как возвести?
К огда я был студентом, мой преподаватель по методам программирования любил повторять: «В математике все идеи простые». Чаще всего, фраза звучала в момент объяснения новой сложной темы, а потому вызывала определённые внутренние противоречия.
С возведением в степень всё не так — это действительно простая операция.
История
Возведение в степень — частный случай умножения, поэтому данную операцию изначально не рассматривали, как самостоятельную. Но уже в работах Диофанта Александрийского степени отведено особое место. В частности «Отец Алгебры» применял понятия кубов и квадратов числа.
Эта операция была известна ещё в древнем Вавилоне, однако современный её вид устоялся лишь в XVII веке.
Как умножение позволяет сократить количество символов сложения:
6 + 6 + 6 + 6 + 6 + 6 = 6 * 6
Так и степень сокращает запись умножения:
До воцарения числового показателя, были и другие варианты его записи. Математики раннего Возрождения использовали буквы. Например, Q обозначала квадрат, а C — куб. Различные формы записи возведения в степень не обошли и языки программирования.
Для АЛГОЛа и некоторых диалектов Бейсика применяется значок ↑. В матлабе, R, Excel-е и Хаскеле используется «циркумфлекс» — ^ или «галочка». Этот символ популярен и вне программирования.
Определение
В Python возведение в степень записывается при помощи двойной «звёздочки» — » ** «
a = 2 ** 4 print(a) > 16
Вторая форма записи — встроенная функция pow():
# первый аргумент — основание, а второй — показатель b = pow(2, 4) print(b) > 16
Обратные операции
Извлечение корня
# корень четвёртой степени из 16 root = pow(16, (1/4)) print(root) > 2.0
Либо с применением оператора » ** «:
# корень кубический из 27 cub_root = 27 ** (1/3) print(cub_root) > 3.0
Для извлечения квадратного корня справедливы оба вышеуказанных способа, но существует и третий, специализированный. Для его применения требуется импортировать модуль math :
import math # квадратный корень из 100 sqr_root = math.sqrt(100) print(sqr_root) > 10.0
Логарифмирование
Логарифмирование — вторая обратная операция.
Логарифмом числа «b» по основанию «a» зовётся такой показатель степени, в который следует возвести «a», чтобы получить «b».
Здесь x — логарифм. Пример из математики — найдем значение выражения:
Легче всего эта запись читается в формате вопроса: «В какую степень нужно возвести 2, чтобы получить 16?». Очевидно, в 4-ю. Следовательно,
В питоне операция нахождения логарифма так же заложена в функционал модуля math:
import math # отыщем логарифм 100 по основанию 10 # 100 — основание логарифма, а 10 — аргумент log = math.log(100, 10) print(log) > 2.0
Степень
Целочисленная
В целочисленную степень можно возводить положительные и отрицательные int и float числа:
И функция pow() и оператор » ** » умеют возводить комплексные числа:
# complex a = complex(2, 1) print(pow(a, 2)) > (3+4j) print(a ** 2) > (3+4j)
Показатель степени может быть положительным, отрицательным и нулевым:
Результат не определён, когда 0 возводят в отрицательную степень:
Ошибка деления на ноль возникает из-за следующего свойства степени:
Рациональная
Возведение числа в рациональную степень напрямую связано с извлечением корня из этого числа отношением:
Если рациональный показатель отрицательный, а основание равно нулю, то Питон все ещё будет выдавать ошибку:
В случае, когда основание меньше нуля, числитель показателя нечётный, а знаменатель, напротив, чётный, результат получается комплексным. Но это свойство рациональных степеней учитывается только в функции pow() :
print(pow(-5, (5/4))) > (-5.286856317202822-5.286856317202821j) print(type(pow(-5, (5/4)))) >
В остальном возведение в рациональную степень работает, как и для целочисленной:
print(0 ** (3/2)) > 0.0 print(pow(1, (23/24))) > 1.0 print(10 ** (6/7)) > 7.196856730011519
Вещественная
В начале автор объявил, что возведение в степень — штука несложная. Так вот, для вещественных степеней это уже не совсем так. Идеи, заложенные в эту операцию, хоть и просты, но их много, и каждая из них достойна собственной статьи. Описать вкратце разложение в ряд Тейлора и численное интегрирование не получится. Это будет не справедливо, как по отношению к вам, так и к математике. Поэтому, выделим главное:
Python умеет возводить в вещественную степень даже вещественные числа (пусть и псевдо)
Сделать такое инструментами математики ой как непросто:
# возведём число Пи в степень e print(pow(math.pi, math.e)) > 22.45915771836104
Ноль в степени ноль
Дискуссии по поводу значения 0 в степени 0 продолжаются уже больше двух веков. Обычно значение нуля в нулевой степени принято считать неопределённым, но символическое соглашение о том, что «0 в степени 0 равно 1» помогает в записи формул и алгоритмов. Ровно поэтому так сделано и в Python:
Возведение в степень
Квадратный корень: math.sqrt () и cmath.sqrt
ValueError: ошибка математического домена
Экспонирование с использованием встроенных функций: ** и pow ()
Для большинства (все в Python 2.x) арифметических операций тип результата будет типом более широкого операнда. Это не верно для ** ; следующие случаи являются исключениями из этого правила:
или можно напрямую вызвать __pow__ метод:
Экспонирование с использованием математического модуля: math.pow()
Что исключает вычисления со сложными входами:
Ошибка типа: невозможно преобразовать сложное в плавающее
и вычисления, которые привели бы к сложным результатам:
ValueError: ошибка математического домена
Экспоненциальная функция: math.exp () и cmath.exp ()
Экспоненциальная функция минус 1: math.expm1()
Для очень маленьких х разница становится больше:
Улучшение является значительным в научных вычислениях. Например, закон Планка содержит экспоненциальную функцию минус 1:
Магические методы и возведение в степень: построение, математика и математика
Предположим, у вас есть класс, который хранит чисто целочисленные значения:
Использование встроенной pow функции или ** оператор всегда вызывает __pow__ :
Второй аргумент __pow__() метод может подаваться только с помощью builtin- pow() или путем непосредственного вызова метода:
Ошибка типа: требуется плавающее число
Модульное возведение в степень: pow() с 3 аргументами
Обеспечение pow() с аргументами 3 pow(a, b, c) оценивает модульного возведения в степень а б мод C:
Для встроенных типов использование модульного возведения в степень возможно только в том случае, если:
Эти ограничения также присутствуют в Python 3.x
Например, можно использовать 3-аргумент форму pow определить модульную обратную функцию:
Корни: n-корень с дробными показателями
В то время как math.sqrt функция предусмотрена для конкретного случая квадратных корней, это часто бывает удобно использовать оператор возведения в степень ( ** ) с дробными показателями для выполнения п-корневые операции, как кубические корни.
Обратное возведение в степень является возведением в степень по взаимности экспоненты. Таким образом, если вы можете кубизировать число, указав его в показателе степени 3, вы можете найти корень куба в числе, указав его в показателе 1/3.
Вычисление больших целочисленных корней
Несмотря на то, что Python изначально поддерживает большие целые числа, получение n-го корня очень больших чисел может привести к сбою в Python.
OverflowError: long int слишком велико для преобразования в float
При работе с такими большими целыми числами вам нужно будет использовать пользовательскую функцию для вычисления n-го корня числа.
Научим основам Python и Data Science на практике
Это не обычный теоритический курс, а онлайн-тренажер, с практикой на примерах рабочих задач, в котором вы можете учиться в любое удобное время 24/7. Вы получите реальный опыт, разрабатывая качественный код и анализируя реальные данные.
вычисление кубического корня в python
Я пытаюсь оценить следующую функцию в python:
4 ответа
Вот простой способ вычисления целого квадратного корня: int isqrt(int num) < int root=0; int b = 0x8000; int a=0, c=0; while (b) < c = a|b; if (c*c >= 1; > > Гениально (спасибо Википедии ), это можно оптимизировать следующим образом: int sqrt(short num) < int op = num;.
Имеет ли F# встроенную функцию кубического корня? Я знаю, что могу использовать возведение в степень для вычисления cuberoots, но в моем случае он не будет проверять тип, так как я хочу взять cuberoot количества типа float и получить float.
Используйте математику с плавающей запятой (1/3 усекается до нуля). Кроме того, нет необходимости в math.pow (** для возведения в степень).
Кроме того, дополнительные пробелы, которые вы добавляете в аргументы вызова функции, противоречат PEP-8 (Руководство по стилю Python). Конкретно этот пункт:
в вашем коде. В противном случае ваш показатель всегда будет равен 0 из-за усечения целых чисел.
Так что, если бы вы запустили это под Python 3.x, вы бы не столкнулись с этой конкретной проблемой.
Я думаю, это потому, что вы выполняете целочисленную арифметику там, где вы действительно собираетесь выполнять арифметику с плавающей запятой. Попробуйте изменить [второй] 1 на 1.0 :
Похожие вопросы:
Кажется, что это не проблема, но у меня есть проблемы, чтобы решить эту проблему: Я хотел бы рассчитать уровень на основе заданных очков опыта (exp). Поэтому я использую формулу кубического корня и.
Я хочу отобразить знак кубического корня в android textview, используя Unicode \u221B., он не отображается на textview, а отображается в корзине журналов. TextView txtcube_sqrt = (TextView).
В моем калькуляторе я использую эти операторы для вычисления квадратного корня и кубического корня. case sqrt root: result = Math.Sqrt(number1); break; case root: result = Math.Pow(number1, (1 /.
Вот простой способ вычисления целого квадратного корня: int isqrt(int num) < int root=0; int b = 0x8000; int a=0, c=0; while (b) < c = a|b; if (c*c >= 1; > > Гениально.
Имеет ли F# встроенную функцию кубического корня? Я знаю, что могу использовать возведение в степень для вычисления cuberoots, но в моем случае он не будет проверять тип, так как я хочу взять.
Я хочу отобразить символ кубического корня в приложении android, которое я разрабатываю. Я попробовал unicode для кубического корня. Но он не отображается как символ кубического корня. Он появляется.
Мне нужно проверить, является ли форма кубом (или может быть). У меня есть общий объем и длина одной стороны. Я начинаю с того, что проверяю, больше ли объем и сторона больше 0, а затем, равен ли.
cube_Num = float(input( X: )) cube_Pow = 0.333 cube_Root = cube_Num**cube_Pow print( Result: + str(round(cube_Root))) Теперь, если я введу 216, это даст мне ans 6, что правильно, но если я введу.
Я новичок в программировании, и у меня есть вопрос. как сделать алгоритм поиска кубического корня в C++ без использования таких функций, как pow(). Пользователь вводит число и количество знаков.