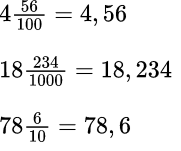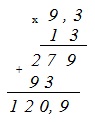Десятичные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Как читать десятичные дроби
В первую очередь обсудим вид десятичной дроби. Каждая цифра после запятой имеет своё название.
Десятые, сотые, тысячные, десятитысячные…
Десятые, сотые и тысячные
Попробуем прочитать десятичную дробь из примера выше. Чтобы правильно прочитать десятичную дробь нужно:
Прочитать число слева от запятой и добавить слово «целыx», так как слева от запятой находится целая часть десятичной дроби. Читаем: «сорок три целых».
Затем прочитать число справа от запятой: «семь тысяч пятьсот шестьдесят девять».
Значит, полное название дроби звучит так:
43,7569 — сорок три целых семь тысяч пятьсот шестьдесят девять десятитысячных.
Справа от запятой после самой последней правой цифры отличной от нуля можно добавлять сколько угодно нулей. От этого значение десятичной дроби не изменится.
Таким же образом если в конце десятичной дроби отбросить ноль, то мы получим такую же по значению десятичную дробь.
Нули можно добавлять (убирать) только после самой последней правой отличной от нуля цифры. Нули между цифрами в числе убирать нельзя.
Десятичные дроби
теория по математике ? числа и вычисления
Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).
Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:
4,56 – четыре целых пятьдесят шесть сотых 18,234 – восемнадцать целых двести тридцать четыре тысячных 78,6 – семьдесят восемь целых шесть десятых
Чтение десятичных дробей
Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять — один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).
Десятичные дроби получаются из обыкновенных дробей:
Сложение (вычитание) десятичных дробей
Чтобы сложить (вычесть) в столбик две десятичные дроби нужно:
Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.
Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.
34,145 + 5,678 = 39,823
Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.
Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.
Умножение десятичных дробей
При умножении двух десятичных дробей в столбик необходимо:
Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.
0,125 × 2,3 00375 0250 0,2875
Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.
Умножение десятичных дробей на 10, 100, 1000…
Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.
Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.
Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.
Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.
Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.
Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.
Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.
Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.
Деление десятичных дробей
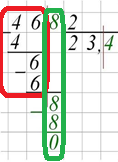
Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4
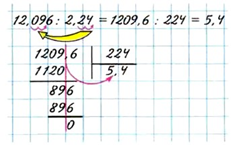
Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.
Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.
Деление десятичной дроби на 10, 100, 1000…
При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.
Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.
Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.
Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.
Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.
Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.

Сформируем из чисел ряд от наименьшего из них до наибольшего. Для этого сначала разделим их на положительные и отрицательные. И сразу получим наибольшее в ряду (поскольку оно единственное больше нуля): 0,021.
Три оставшихся отрицательных распределим по их модулям. Известно, что из двух отрицательных чисел больше то, у которого модуль меньше. Тогда получаем, что –0,304
pазбирался: Даниил Романович | обсудить разбор | оценить
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Это задание требует простого умения выполнять арифметические действия с десятичными дробями.
Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:
Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:
Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
Можно произвести вычисления в столбик, тогда получим:
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции — деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
pазбирался: Даниил Романович | обсудить разбор | оценить
Поиск ответа
| Вопрос № 307952 |
Здравствуйте. Задаю свой вопрос во второй раз и все же надеюсь, что вы мне ответите. Возможно ли сокращение слов » десятич ный» и «шестнадцатеричный» таким образом: 10-тичный, 16-теричный? И если нет, то возможно ли в принципе написание этих слов в буквенно-цифровой форме? Я знаю об общем правиле сокращения слов, включающих в себя числа, типа 150-летие или 20-тонный. Однако конкретно таких слов в буквенно-цифровом виде я не видела и очень сильно сомневаюсь, что их можно писать подобным образом. Автор текста настаивает на сокращении.
Ответ справочной службы русского языка
Такие сокращения не являются общепринятыми, они будут непонятны читателю. Наша рекомендация — не сокращать.
Добрый день! Подскажите, пожалуйста, как правильно написать словами «74-километровый»: семи десятич етырехкилометровый или семидесяти четырехкилометровый?
Ответ справочной службы русского языка
Правильно: семи десятич етырехкилометровый.
Ответ справочной службы русского языка
В сочетании с дробным числительным существительное ставится в форме единственного числа родительного падежа.
Здравствуйте! Подскажите, каким правилом руководствоваться, когда формируются фразы «в N раз(а)», где N – число с десятич ными долями. Например: в 1,5 разА, в 2,7 раз(А?) и т.п.
Ответ справочной службы русского языка
При дробных числах существительные ставятся в форме единственного числа родительного падежа: в 1,5 раза, в 2,7 раза.
Добрый день, уважаемые эксперты. Я патрулирующий русской Википедии. В своей работе нередко сталкиваюсь с числительными, а именно с денежными наименованиями. Постоянно возникают трудности с десятич ными дробями. Не знаю как склонять существительные рядом с ними. Например, 2,89 миллиардА или миллиардОВ доллара(-ов). Обычно проверяю себя, проговаривая дробное число: «Две целых восемьдесят девять сотЫХ миллиардОВ долларОВ», но не знаю, правильно ли это. Можете, пожалуйста, объяснить и просклонять данное число и, например одна целая тридцать одна сотая. Благодарю.
Ответ справочной службы русского языка
Правило простое: при дробных числительных существительное употребляется в форме единственного числа родительного падежа: 4,3 рубля, 67,84 километра, 2,89 миллиарда. Слово доллар уже не зависит напрямую от числительного, поэтому ставится во множественном числе: 2,89 миллиарда (чего?) долларов.
Поэтому верно: Две целых восемьдесят девять сотых миллиарда долларов; одна целая тридцать одна сотая миллиарда долларов.
Доброго времени суток! Возникла трудность со склонением десятич ных дробей, и ответ найти самостоятельно не получилось. Ниже представлен пример предложения. Прошу помочь разобраться с этим. Если масса половины кубического дециметра вещества равна нулю целым сорока пяти сотым килограмма, то масса одного кубического дециметра вещества равна нулю целых девять десятых килограмма. (Написано по-разному для наглядности вариантов). Спасибо за помощь!
Ответ справочной службы русского языка
Склоняются все части числительного. Верно: Если масса половины кубического дециметра вещества равна нулю целым сорока пяти сотым килограмма, то масса одного кубического дециметра вещества равна нулю целым девяти десятым килограмма.
Обратите внимание, что слова ноль целых обычно опускаются.
Ответ справочной службы русского языка
Союз не нужен: десять целых пять десятых.
Ответ справочной службы русского языка
В русском языке в дробных числах ставится запятая, а не точка. Например: 6,87.
Уважаемые специалисты! Я уже задавала Вам похожий вопрос и получила на него ответ, за что Вам очень благодарна. Большое спасибо! Позвольте, пожалуйста, вопрос ради уточнения. Дело в том, что я не могу найти похожий вопрос среди других вопросов на Вашей сайте. После десятич ных дробей имя существительное всегда стоит в родительном падеже единственном числе. Например, три целых две десятых яблока или семь целых четыре десятых окна. Верно? А вот например, три целых две десятых тысячи автомобилей или семь целых четыре десятых миллиона дорог. Второе имя существительное «автомобилей» и «дорог» всегда стоит в родительном падеже множественном числе? Правило о том, что один автомобиль; два, три, четыре автомобиля; пять, шесть и т. д. автомобилей сюда не подходит? Очень прошу ответить на мой вопрос! Пожалуйста! Заранее благодарю Вас.
Ответ справочной службы русского языка
Правильно, например: три яблока, три целых две десятых яблока, три целых две десятых тысячи яблок; пять яблок, пять целых семь десятых яблока, пять целых семь десятых миллиона яблок.
Объясните, пожалуйста. Мой вопрос касается имён существительных, которые употребляются после десятич ный дробей. Как будет правильно? Семь целых шесть десятых ЯБЛОКА или ЯБЛОК? Восемь целых пять десятых ТЫСЯЧИ или ТЫСЯЧ? Восемь целых пять десятых ТЫСЯЧИ или ТЫСЯЧ автомобилей? Заранее благодарю за ответ!
Ответ справочной службы русского языка
Существительным управляет дробная часть: семь целых шесть десятых яблока, восемь целых пять десятых тысячи автомобилей.
Меня интересуют окончания слов после десятич ных дробей: 422,8 квадратн(ых, ого) метр(ов, а). Ответ нужен срочно.
Ответ справочной службы русского языка
Существительным управляет дробная часть: 422,8 квадратного метра (восемь десятых чего? квадратного метра).
Скажите пожалуйста, какой вариант правильнее использовать с десятич ными дробями: миллиардА или миллиардОВ (миллионА или миллионОВ). Напр. 3,5 миллиарда/миллиардов, 8,2 миллиарда/миллиардов, 21,7 миллиона/миллионов. Зависит ли правильная форма от конкретной цифры? Если да, подскажите пожалуйста общее правило. Спасибо!
Ответ справочной службы русского языка
Существительным управляет дробная часть, поэтому нужен родительный падеж единственного числа: 3,5 миллиарда, 8,2 миллиарда, 21,7 миллиона (пять десятых миллиарда, две десятых миллиарда, семь десятых миллиона).
Здравствуйте. Существует ли какое-то правило по поводу произношения (выбора) «года» или «лет» в десятич ных дробях? Например, «Средний возраст составляет 30.4 года» и
«Повысился до 30.4 лет». Спасибо.
P.S. В корректности примеров не уверен.
Ответ справочной службы русского языка
Если в словосочетании существительное зависит от дробного числительного, то существительное ставится в форме родительного падежа единственного числа: 30,4 года; до 30,4 года.
Ответ справочной службы русского языка
Не следует использовать один и тот же знак как знак перечисления и как знак-разделитель между целой и дробной частью числа. Постановка точки с запятой оправданна.
Подскажите, пожалуйста, как написать «84-пушечный корабль» прописью.
С уважением, Мария
Ответ справочной службы русского языка