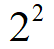Вычислить квадратный корень из числа

Необходимо произвести сложные расчеты, а электронного вычислительного устройства под рукой не оказалось? Воспользуйтесь онлайн программой — калькулятором корней. Она поможет:
| Число знаков после запятой: |
| √ |
Что такое квадратный корень
Корень n степени натурального числа a — число, n степень которого равна a (подкоренное число). Обозначается корень символом √. Его называют радикалом.
Каждое математическое действие имеет противодействие: сложение→вычитание, умножение→деление, возведение в степень→извлечение корня.
Квадратным корнем из числа a будет число, квадрат которого равен a. Из этого следует ответ на вопрос, как вычислить корень из числа? Нужно подобрать число, которое во второй степени будет равно значению под корнем.
Обычно 2 не пишут над знаком корня. Поскольку это самая маленькая степень, а соответственно если нет числа, то подразумевается показатель 2. Решаем: чтобы вычислить корень квадратный из 16, нужно найти число, при возведении которого во вторую степень получиться 16.
Проводим расчеты вручную
Вычисления методом разложения на простые множители выполняется двумя способами, в зависимости от того, какое подкоренное число:
1.Целое, которое можно разложить на квадратные множители и получить точный ответ.
Квадратные числа — числа, из которых можно извлечь корень без остатка. А множители — числа, которые при перемножении дают исходное число.
25, 36, 49 — квадратные числа, поскольку:
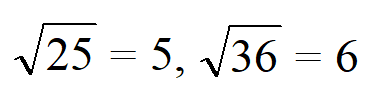
Получается, что квадратные множители — множители, которые являются квадратными числами.
Возьмем 784 и извлечем из него корень.
| Раскладываем число на квадратные множители. Число 784 кратно 4, значит первый квадратный множитель — 4 x 4 = 16. Делим 784 на 16 получаем 49 — это тоже квадратное число 7 x 7 = 16. | 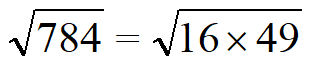 |
| Применим правило Извлекаем корень из каждого квадратного множителя, умножаем результаты и получаем ответ. | 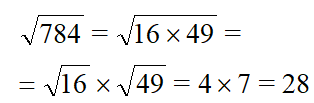 Ответ. |
2.Неделимое. Его нельзя разложить на квадратные множители.
Такие примеры встречаются чаще, чем с целыми числами. Их решение не будет точным, другими словами целым. Оно будет дробным и приблизительным. Упростить задачу поможет разложение подкоренного числа на квадратный множитель и число, из которого извлечь квадратный корень нельзя.
| Раскладываем число 252 на квадратный и обычный множитель. | 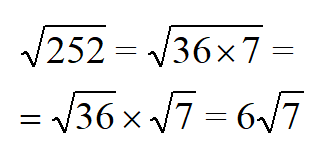 |
| Оцениваем значение корня. Для этого подбираем два квадратных числа, которые стоят впереди и сзади подкоренного числа в цифровой линейки. | Подкоренное число — 7. Значит ближайшее большее квадратное число будет 8, а меньшее 4.
|
| Оцениваем значение | Вероятнее √7 ближе к 2. Подбираем таким образом, чтобы при умножении этого числа на само себя получилось 7. 2,7 x 2,7 = 7,2. Не подходит, так как 7,2>7, берем меньшее 2,6 x 2,6 = 6,76. Оставляем, ведь 6,76 7. |
| Вычисляем корень | 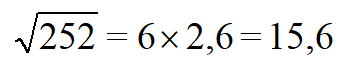 |
Как вычислить корень из сложного числа? Тоже методом оценивая значения корня.
При делении в столбик получается максимально точный ответ при извлечении корня.
| Возьмите лист бумаги и расчертите его так, чтобы вертикальная линия находилась посередине, а горизонтальная была с ее правой стороны и ниже начала. |  |
| Разбейте подкоренное число на пары чисел. Десятичные дроби делят так: — целую часть справа налево; — число после запятой слева направо. | Пример: 3459842,825694 → 3 45 98 42, 82 56 94 Допускается, что вначале остается непарное число. |
| Для первого числа (или пары) подбираем наибольшее число n. Его квадрат должен быть меньше или равен значению первого числа (пары чисел). Извлеките из этого числа корень — √n. Запишите полученный результат сверху справа, а квадрат этого числа — снизу справа. У нас первая 7. Ближайшее квадратное число — 4. Оно меньше 7, а 4 = | 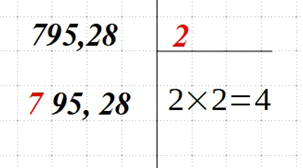 |
| Вычтите найденный квадрат числа n из первого числа (пары). Результат запишите под 7. А верхнее число справа удвойте и запишите справа выражение 4_х_=_. Примечание: числа должны быть одинаковыми. | 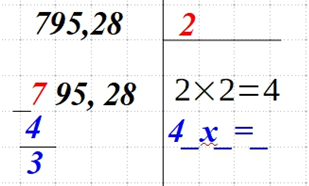 |
| Подбираем число для выражения с прочерками. Для этого найдите такое число, чтобы полученное произведение не было больше или равнялось текущему числу слева. В нашем случае это 8. | 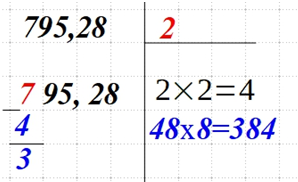 |
| Запишите найденное число в верхнем правом углу. Это второе число из искомого корня. Снесите следующую пару чисел и запишите возле полученной разницы слева. | 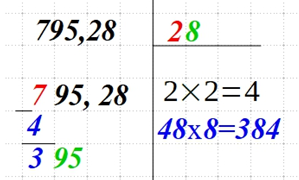 |
| Вычтите полученное справа произведение из числа слева. Удваиваем число, которое расположено справа вверху и записываем выражение с прочерками. | 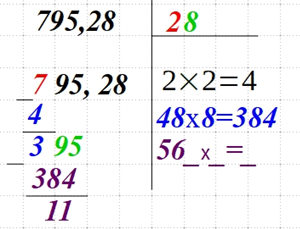 |
| Сносим к получившейся разнице еще пару чисел. Если это числа дробной части, то есть расположены за запятой, то и в верхнем правом углу возле последней цифры искомого квадратного корня ставим запятую. Заполняем прочерки в выражении справа, подбирая число так, чтобы полученное произведение было меньше или равно разницы выражения слева. | 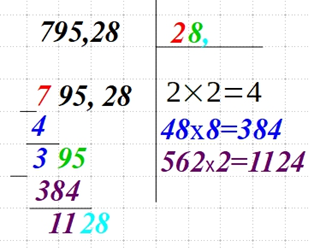 |
| Если необходимо большее количества знаков после запятой, то дописывайте возле текущей цифры слева и повторяйте действия: вычитание слева, удваиваем число в верхнем правом углу, записываем выражение прочерками, подбираем множители для него и так далее. | 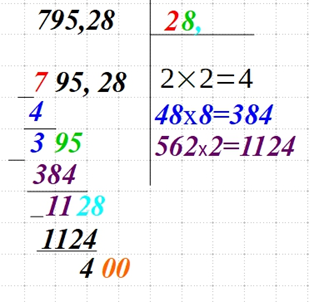 |
Как думаете сколько времени вы потратите на такие расчеты? Сложно, долго, запутанно. Тогда почему бы не упростить себе задачу? Воспользуйтесь нашей программой, которая поможет произвести быстрые и точные расчеты.
1. Введите желаемое количество знаков после запятой.
2. Укажите степень корня (если он больше 2).
3. Введите число, из которого планируете извлечь корень.
Примеры слов с чередующимися гласными е/и в корне
Приведем примеры слов с чередующимися гласными «е», «и» в корне.
В корне некоторых слов в безударной позиции пишется то буква «е», то «и», например:
Как правильно написать эти слова? В этих случаях невозможно проверить безударные гласные в корне слов с помощью ударения, подобрав родственные слова или изменив форму слова. В корне подобных слов отметим чередование гласных е//и.
Правило написания е/и в корнях слов с чередованием гласных
Чтобы выбрать правильное написание слов с чередующимися гласными е//и в корне, руководствуемся орфографическим правилом.
Например:
Поможет в написании таких слов стишок-запоминалка:
Собирать, стирать, задира —
Повнимательней гляди!
Если в слове имя Ира,
Значит, в корне буква «и».
Если после корня «а»,
В корне будет «и» всегда.
Вот пример, запоминай:
— Ноги вытер? — вытирай!
Слова с чередующимися гласными е//и в корне
1. бер-/бир-
2. дер-/дир-
3. мер-/мир-
4. пер-/пир-
5. тер-/тир-
6. блест-/блист-
7. жег-/жиг-
8. стел-/стил-
9. чет-/чит-
Дополнительный материалПримеры слов с корнем раст-/ращ-/рос-.
Примеры слов с корнем бер-/бир-.
Примеры слов с корнем лаг-/лож-.
Примеры слов с корнем гар-/гор-.
Примеры слов с корнями кас-/кос-.
Примеры слов с корнями зар-/зор-.
Вычесть как пишется корень
Перечень (по алфавиту корней, приставочные глаголы приводятся выборочно):
выб и рать, заб и рать, разб и рать, поб и раться — б е ру, б е ри, выб е ри, заб е ру — брать, выбрать, забрать;
перев и рать, зав и раться — врать, переврать, завраться, вру, перевру, заврётся;
зад и рать, разд и рать, прид и раться, уд и рать — д е ру, д е ри, зад е ру, разд е ру, уд е ру — драть, разодрать, придраться, удрать;
выж и гать, прож и гать, обж и гать, отж и гать, разж и гать — выж е г (прош. время), выж е чь — жгу, выжгу, прожгу;
ож и дать, переж и дать, подж и дать — ждать, переждать, подождать, жду, пережду, подожду;
заж и мать, приж и мать — жму, сожму, прижму;
наж и нать, пож и нать — жну, нажну, пожну;
пож и рать, обж и раться — жрать, пожрать, обожраться, жру, пожру, обожрётся;
зап и наться — запнуться, запнусь;
вз и рать, надз и рать, оз и раться, през и рать — соз е рцать — зреть (‘смотреть, видеть’, устар.), прозреть, узреть, зрю, прозрю, узрю, зрение, презрение;
подм и нать, см и нать, разм и нать — мну, подомну, сомну, разомну;
зам и рать, пом и рать, ум и рать — зам е реть, пом е реть, ум е реть, зам е р, ум е р, зам е рший — мрут, замру, помру, умру; пинать — пнуть, пну;
зап и рать, отп и рать, уп и раться — зап е реть, зап е р, взап е рти, отп е реть, уп е реться, п е рила — запру, отопру, упрётся;
пом и нать, вспом и нать, запом и нать, припом и нать — помнить, вспомнить, запомнить, вспомню, запомню;
поп и рать — попрать, попрут;
преп и раться — прения, распря;
прост и рать (протягивать (руки); распространять), прост и раться — прост е реть, прост е реться — простру, прострётся (устарелые формы);
расп и нать — распну;
соз и дать — создать;
выст и лать, заст и лать, расст и лать — ст е лить, выст е лить, заст е лить, пост е лить, расст е лить — стлать, выстлать, застлать, постлать, разостлать;
нат и рать, раст и рать, зат и рать — т е реть, нат е реть, раст е реть, зат е реть — тру, натру, разотру, трение;
нач и нать, зач и нать — начну, зачну;
выч и тать, сч и тать (вести счет), пересч и тать, просч и тать, рассч и тать — выч е т, выч е сть, выч е л — вычту, сочту (сосчитаю), начту, перечту (пересчитаю);
поч и тать (относиться с почтением), предпоч и тать — поч е сть — чтить, почтить, чту, почту, предпочту, почтенный, почтение, почтительный, предпочтение;
ч и тать, проч и тать, переч и тать — прочту, перечту, чтение, чтец.
Примечание 5. В словах, однокоренных с помина́ть, вспомина́ть, по́мнить — в глаголах помяну́ть, вспомян́уть, упомяну́ть, пишется в безударном положении буква я (то же под ударением: ср. помя́нет, вспомя́нет, упомя́нуты и т. п.).
Действие с корнями: сложение и вычитание. Как вычесть корень из числа
В математике любое действие имеет свою пару-противоположность – в сущности, это представляет собою одно из проявлений гегелевского закона диалектики: «единство и борьба противоположностей». Одно из действий в такой «паре» направлено на увеличение числа, а другое, обратное ему – на уменьшение. Например, действие, противоположное сложению – это вычитание, умножению соответствует деление. Имеется и своя диалектическая пара-противоположность и у возведения в степень. Речь идет об извлечении корня.
Извлечь из числа корень такой-то степени – это значит вычислить, какое число необходимо возвести в соответствующую степень, чтобы в итоге получилось данное число. Две степени имеют свои отдельные названия: вторая степень называется «квадратом», а третья – «кубом». Соответствено, корни данных степеней приятно именовать квадратным корнем и кубическим. Действия с кубическими корнями – тема для отдельного разговора, а сейчас поговорим о сложении квадратных корней.
Начнем с того, что в ряде случаев квадратные корни проще сначала извлечь, а потом уже складывать результаты. Предположим, нам необходимо найти значение такого выражения:
Ведь совсем не сложно вычислить, что корень квадратный из 16 равен 4, а из 121 – 11. Следовательно,
Впрочем, это самый простой случай – здесь речь идет о полных квадратах, т.е. о таких числах, которые получаются при возведении в квадрат целых чисел. Но так бывает не всегда. Например, число 24 – это не полный квадрат (не найти такого целого числа, которое при возведении его во вторую степень дало бы в результате 24). То же самое относится к такому числу, как 54… Что делать, если нам необходимо сложить корни квадратные из этих чисел?
В таком случае мы получим в ответе не число, а другое выражение. Максимум, что мы можем тут сделать – это максимально упростить исходное выражение. Для этого придется вынести множители из-под корня квадратного. Посмотрим, как это делается, на примере упомянутым чисел:
Для начала разложим на множители 24 – таким образом, чтобы из одного из них легко можно было извлечь корень квадратный (т.е., чтобы он был полным квадратом). Такое числи есть – это 4:
Теперь проделаем то же самое с 54. В его составе таким числом будет 9:
Т.о., у нас получается следующее:
Теперь извлечем корни из того, из чего можем их извлечь: 2*√6+3*√6
Здесь есть общий множитель, который мы можем вынести за скобки:
Это и будет результатом сложения – больше ничего тут извлечь нельзя.
Правда, можно прибегнуть к помощи калькулятора – правда, результат будет приблизительным и с огромным количеством знаков после запятой:
Постепенно округляя его, мы получим приблизительно 2,5. Если нам все-таки хотелось бы довести до логического завершения решение предыдущего примера, мы можем умножить этот результат на 5 – и получится у нас 12,5. Более точного результата при таких исходных данных получить нельзя.
В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Обозначение корней. Выражение под знаком корня () означает, что из этого выражения необходимо извлечь корень определенной степени.
Запомните, какие корни можно складывать, а какие нельзя. Так же, как нельзя складывать разные члены выражения, например, 2а + 2b 4ab, вы не можете складывать разные корни.
Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения. Например, рассмотрим выражение:
2 (3) + (81) + 2 (50) + (32) + 6 (3)
Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.
Число, которое находится под знаком корня, часто мешает решению уравнения, с ним неудобно работать. Даже если оно возведено в степень, дробно или не может быть представлено в виде целого числа в определенной степени, можно попытаться вывести его из…
Корнем из числа x называется такое число, которое при возведении в степень корня будет равно x. Множителем называется умножаемое число. То есть, в выражении вида x*ª-&radic-y нужно внести x под корень. Инструкция 1Определите степень…
Если подкоренное выражение содержит набор математических действий с переменными, то иногда в результате его упрощения есть возможность получить относительно простое значение, часть которого можно вынести из под корня. Бывает полезно такое упрощение…
Арифметические действия с корнями различной степени могут значительно упростить расчеты в физике и технике и сделать их более точными. При умножении и делении удобнее не извлекать корень из каждого сомножителя или делимого и делителя, а сначала…
Квадратным корнем из числа x называют число a, которое при умножении само на себя дает число x: a * a = a^2 = x, x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания. Инструкция …
При выполнении различных арифметических действий с корнями часто бывает необходимо умение преобразовывать подкоренные выражения. Для упрощения расчетов может понадобиться вынести множитель за знак радикала или внести под него. Это действие можно…
Корнем называют значок, обозначающий математическую операцию нахождения такого числа, возведение которого в указанную перед знаком корня степень должно дать число, указанное под этим самым знаком. Часто для решения задач, в которых присутствуют…
Знаком корня в математических науках называется условное обозначение для корней. Число, находящееся под знаком корня, называется подкоренным выражением. При отсутствии показателя степени корень является квадратным, в противном случае цифра указывает…
Арифметическим корнем n-й степени из действительного числа a называют такое неотрицательное число x, n-я степень которого равна числу a. Т.е. (n) a = x, x^n = a. Существуют различные способы сложения арифметического корня и рационального числа.…
Инструкция
Полезный совет
Если вы раскладываете число на множители, дабы перенести квадрат из под знака корня, то совершите обратную проверку — перемножьте все получившиеся множители и получите изначальное число.
В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Часть 1 Определение корней
Часть 2 Упрощение и сложение корней
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. «)
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
можно познакомиться с функциями и производными.
Вычесть как пишется корень
Перечень (по алфавиту корней, приставочные глаголы приводятся выборочно):
выб и рать, заб и рать, разб и рать, поб и раться — б е ру, б е ри, выб е ри, заб е ру — брать, выбрать, забрать;
перев и рать, зав и раться — врать, переврать, завраться, вру, перевру, заврётся;
зад и рать, разд и рать, прид и раться, уд и рать — д е ру, д е ри, зад е ру, разд е ру, уд е ру — драть, разодрать, придраться, удрать;
выж и гать, прож и гать, обж и гать, отж и гать, разж и гать — выж е г (прош. время), выж е чь — жгу, выжгу, прожгу;
ож и дать, переж и дать, подж и дать — ждать, переждать, подождать, жду, пережду, подожду;
заж и мать, приж и мать — жму, сожму, прижму;
наж и нать, пож и нать — жну, нажну, пожну;
пож и рать, обж и раться — жрать, пожрать, обожраться, жру, пожру, обожрётся;
зап и наться — запнуться, запнусь;
вз и рать, надз и рать, оз и раться, през и рать — соз е рцать — зреть (‘смотреть, видеть’, устар.), прозреть, узреть, зрю, прозрю, узрю, зрение, презрение;
подм и нать, см и нать, разм и нать — мну, подомну, сомну, разомну;
зам и рать, пом и рать, ум и рать — зам е реть, пом е реть, ум е реть, зам е р, ум е р, зам е рший — мрут, замру, помру, умру; пинать — пнуть, пну;
зап и рать, отп и рать, уп и раться — зап е реть, зап е р, взап е рти, отп е реть, уп е реться, п е рила — запру, отопру, упрётся;
пом и нать, вспом и нать, запом и нать, припом и нать — помнить, вспомнить, запомнить, вспомню, запомню;
поп и рать — попрать, попрут;
преп и раться — прения, распря;
прост и рать (протягивать (руки); распространять), прост и раться — прост е реть, прост е реться — простру, прострётся (устарелые формы);
расп и нать — распну;
соз и дать — создать;
выст и лать, заст и лать, расст и лать — ст е лить, выст е лить, заст е лить, пост е лить, расст е лить — стлать, выстлать, застлать, постлать, разостлать;
нат и рать, раст и рать, зат и рать — т е реть, нат е реть, раст е реть, зат е реть — тру, натру, разотру, трение;
нач и нать, зач и нать — начну, зачну;
выч и тать, сч и тать (вести счет), пересч и тать, просч и тать, рассч и тать — выч е т, выч е сть, выч е л — вычту, сочту (сосчитаю), начту, перечту (пересчитаю);
поч и тать (относиться с почтением), предпоч и тать — поч е сть — чтить, почтить, чту, почту, предпочту, почтенный, почтение, почтительный, предпочтение;
ч и тать, проч и тать, переч и тать — прочту, перечту, чтение, чтец.
Примечание 5. В словах, однокоренных с помина́ть, вспомина́ть, по́мнить — в глаголах помяну́ть, вспомян́уть, упомяну́ть, пишется в безударном положении буква я (то же под ударением: ср. помя́нет, вспомя́нет, упомя́нуты и т. п.).
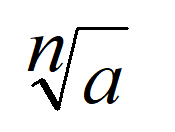
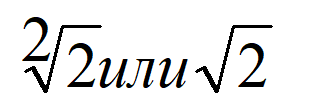
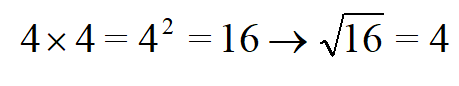
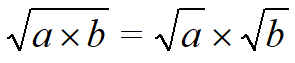
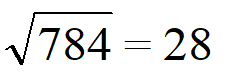
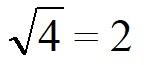
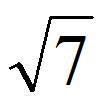 между 2 и 4.
между 2 и 4.