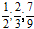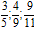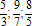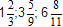Калькулятор дробей
Как перевести смешанную дробь в обыкновенную
Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя: i n d = i · d + n d
5 3 4 = 5 · 4 + 3 4 = 23 4
Как перевести обыкновенную дробь в смешанную
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Как перевести десятичную дробь в обыкновенную или смешанную
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
Например, переведем 0.36 в обыкновенную дробь:
Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
Умножение дробей
Алгоритм действий при умножении двух дробей:
Деление дробей
Алгоритм действий при делении двух дробей:
Дроби
Что такое дробь? Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы.
По способу записи дроби делятся на два формата: обыкновенные вида 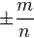
Примеры обыкновенных дробей:
Правильные дроби
Дробь называется правильной, если модуль числителя меньше модуля знаменателя.
Примеры правильных дробей:
Расчеты и формулы дробей онлайн
Неправильные дроби
Дробь называется неправильной, если модуль числителя больше модуля знаменателя.
Примеры неправильных дробей:
Смешанные числа
Запись числа, содержащую целую и дробную части, называют смешанным числом.
Смешанное число можно представить в виде неправильной дроби.
Примеры смешанных чисел:
Десятичные дроби
Бывают задания, когда перевод обыкновенной дроби в десятичную просто необходим.
Десятичная дробь, это дробь которая записывается без знаменателя.
Посмотреть перевод обыкновенной дроби в десятичную можно здесь
Примеры десятичных дробей: 0,1; 0,13; 0,121.
Общий знаменатель дробей онлайн
Калькулятор приводит несколько дробей к общему знаменателю. Просто введите дроби и получите подробное решение и ответ. Можно вводить две, три дроби и более. Числители и знаменатели дробей должны быть натуральными числами.
Как привести дроби к общему знаменателю?
Чтобы выполнить с дробями такие операции, как сравнение, сложение и вычитание, дроби нужно привести к общему знаменателю.
Пример. Привести к общему знаменателю дроби и
Решение. Находим наименьшее общее кратное знаменателей дробей. НОК(12, 8) = 24. Это число и будет новым знаменателем.
Чтобы знаменатели обеих дробей стали равны 24, числитель и знаменатель первой дроби нужно домножить на 2 = 24:12, а числитель и знаменатель второй дроби — на 3 = 24:8.
Приводим к общему знаменателю первую дробь:
Приводим к общему знаменателю вторую дробь:
Общий знаменатель трёх дробей
Если к общему знаменателю требуется привести три дроби и более, то алгоритм действий в таком случае аналогичен алгоритму для двух дробей.
Чтобы разобраться лучше, рассмотрим пример.
Пример. Привести к общему знаменателю три дроби
и
Решение. Сначала найдём наименьшее общее кратное знаменателей дробей. Число 12 делится на знаменатели всех дробей, и это наименьшее такое число. Поэтому НОК(3, 4, 6) = 12. Число 12 будет новым знаменателем.
Чтобы знаменатели дробей стали равны 12, числитель и знаменатель первой дроби нужно домножить на 4 = 12:3, числитель и знаменатель второй дроби — на 3 = 12:4, а числитель и знаменатель третьей дроби — на 2 = 12:6.
Приводим дроби к общему знаменателю и получаем:
Всё — дроби приведены! Пожалуй, самая большая сложность — правильно найти (или угадать) число, которое будет новым знаменателем.
Дроби. Вычитание дробей.
Вычитание дробей с одинаковыми знаменателями.
Для нахождения разницы 2х дробей с одинаковыми знаменателями, необходимо вычесть из числителя 1й дроби числитель 2й дроби, а знаменатель обоих дробей оставить не изменяя. Вычитание обыкновенных дробей:
Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь, которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:


Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной, единицу переводят к виду неправильной дроби, у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7, т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей – правильной из целого числа (натурального числа) :
Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей.
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ), и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители, то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Общий знаменатель дробей онлайн
Калькулятор приводит несколько дробей к общему знаменателю. Просто введите дроби и получите подробное решение и ответ. Можно вводить две, три дроби и более. Числители и знаменатели дробей должны быть натуральными числами.
Как привести дроби к общему знаменателю?
Чтобы выполнить с дробями такие операции, как сравнение, сложение и вычитание, дроби нужно привести к общему знаменателю.
Пример. Привести к общему знаменателю дроби и
Решение. Находим наименьшее общее кратное знаменателей дробей. НОК(12, 8) = 24. Это число и будет новым знаменателем.
Чтобы знаменатели обеих дробей стали равны 24, числитель и знаменатель первой дроби нужно домножить на 2 = 24:12, а числитель и знаменатель второй дроби — на 3 = 24:8.
Приводим к общему знаменателю первую дробь:
Приводим к общему знаменателю вторую дробь:
Общий знаменатель трёх дробей
Если к общему знаменателю требуется привести три дроби и более, то алгоритм действий в таком случае аналогичен алгоритму для двух дробей.
Чтобы разобраться лучше, рассмотрим пример.
Пример. Привести к общему знаменателю три дроби
и
Решение. Сначала найдём наименьшее общее кратное знаменателей дробей. Число 12 делится на знаменатели всех дробей, и это наименьшее такое число. Поэтому НОК(3, 4, 6) = 12. Число 12 будет новым знаменателем.
Чтобы знаменатели дробей стали равны 12, числитель и знаменатель первой дроби нужно домножить на 4 = 12:3, числитель и знаменатель второй дроби — на 3 = 12:4, а числитель и знаменатель третьей дроби — на 2 = 12:6.
Приводим дроби к общему знаменателю и получаем:
Всё — дроби приведены! Пожалуй, самая большая сложность — правильно найти (или угадать) число, которое будет новым знаменателем.