Функции Sqrt и Sqr
Подпишись на новости, чтобы ничего не пропустить
Функция Sqrt в Паскале вычисляет квадратный корень числа. Синтаксис функции следующий:
function Sqrt(Х : ValReal) : ValReal;
Эта функция возвращает квадратный корень числа, переданного через параметр Х. Число Х должно быть положительным, иначе произойдёт ошибка во время выполнения программы (так написано в документации, но в моей версии компилятора ошибки не происходит, а функция в случае отрицательного параметра возвращает значение NaN).
Функция Sqr в Паскале вычисляет квадрат числа. Синтаксис функции для разных типов приведён ниже:
Эта функция возвращает результат вычисления квадрата числа, переданного через параметр. То есть Sqr = х * х.
О типе ValReal я рассказывал здесь.
Квадрат числа
Здесь всё крайне просто. Квадрат числа Х равен произведению Х на Х. То есть функция Sqr на первый взгляд кажется бесполезной. Потому что во многих случаях проще написать так:
Единственный случай, когда использование функции Sqr является обоснованным с точки зрения упрощения кода, это когда в качестве параметра передаётся вещественное число (константа) с большим количеством знаков после запятой, или очень большое целое число, или сложное выражение. Например:
будет написать проще, чем
Х := 5.3456753322 * 5.3456753322
Также возведение в квадрат числа в Паскале сложного выражения тоже будет проще, если использовать функцию Sqr:
X := Sqr(Y + 100 * Z / X)
Вычисление квадратного корня
Когда мы изучали функции вычисления экспоненты и натурального логарифма, то мы узнали, что с их помощью можно возвести число в любую степень. То есть вычислить, в том числе, и корень любой степени.
Однако использование этих функций всё-таки немного сложновато. Поэтому для вычисления квадратного корня в Паскале имеется специальная функция (потому что квадратный корень приходится вычислять намного чаще, чем, например, корень n-й степени).
А здесь я напомню что такое квадратный корень для тех, кто подзабыл математику.
То есть квадратный корень из числа А, это число Х, которое при возведении в квадрат даёт число А.
ВАЖНО!
Число А может быть только положительным числом. Извлечение корня из отрицательного числа тоже возможно, но это уже будут комплексные числа.
Pascal: Занятие №1. Часть 3: Типы данных в Паскаль
Типы данных в Паскале
Паскаль — это типизированный язык программирования. Это означает, что переменные, в которых хранятся данные, имеют определенный тип данных. Т.е. программе напрямую надо указать, какие данные могут храниться в той или иной переменной: текстовые данные, числовые данные, если числовые — то целочисленные или дробные, и т.п. Это необходимо в первую очередь для того чтобы компьютер «знал», какие операции можно выполнять с этими переменными и как правильно их выполнять.
Например, сложение текстовых данных, или как это правильно называется в программировании — конкатенация — это обычное слияние строк, тогда как сложение числовых данных происходит поразрядно, кроме того, дробные и целые числа складываются тоже по-разному. То же самое касается и других операций.
Рассмотрим наиболее распространенные в Pascal типы данных.
Целочисленные типы данных в Паскаль
| Тип | Диапазон | Требуемая память (байт) |
| byte | 0..255 | 1 |
| shortint | -128..127 | 1 |
| integer | -32768.. 32767 | 2 |
| word | 0..65535 | 2 |
| longint | -2147483648..2147483647 | 4 |
Нужно иметь в виду, что при написании программ в паскале integer (в переводе с англ. целое) является наиболее часто используемым, так как диапазон значений наиболее востребуем. Если необходим более широкий диапазон, используется longint (long integer, в переводе с англ. длинное целое). Тип byte в Паскале используется, когда нет необходимости работать с отрицательными значениями, то же самое касается и типа word (только диапазон значений здесь значительно больше).
Примеры того, как описываются (объявляются) переменные в Паскале:
| Pascal | PascalABC.NET | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Pascal | PascalABC.NET | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ДЕЙСТВИЕ | РЕЗУЛЬТАТ | СМЫСЛ |
|---|---|---|
| 2 + 3 | 5 | плюс |
| 4 — 1 | 3 | минус |
| 2 * 3 | 6 | умножить |
| 17 div 5 | 3 | целочисленное деление |
| 17 mod 5 | 2 | остаток от целочисленного деления |
Порядок выполнения операций
var a: integer; b: real; begin a := 1; writeln(‘a := 1; a = ‘,a); a += 2; // Увеличение на 2 writeln(‘a += 2; a = ‘,a); a *= 3; // Умножение на 3 writeln(‘a *= 3; a = ‘,a); writeln; b := 6; writeln(‘b := 6; b = ‘,b); r /= 2; writeln(‘b /= 2; b = ‘,b); end.
Стандартные арифметические процедуры и функции Pascal
Здесь стоит более подробно остановиться на некоторых арифметических операциях.
Пример операции inc:
Более сложное использование процедуры inc:
Inc(x,n) где x — порядкового типа, n — целого типа; процедура inc увеличивает x на n.
Пример использования функции odd:
begin WriteLn(Odd(5));
Пример использования процедуры sqr в Pascal:
var x:integer; begin x:=3; writeln(sqr(x)); <ответ 9>end.
Однако в компиляторе pascal abc возведение в степень осуществляется значительно проще:
Пример использования процедуры sqrt в Pascal:
var x:integer; begin x:=9; writeln(sqrt(x)); <ответ 3>end.
Pascal-Паскаль
Программирование. Графика Pascal-Паскаль
Программирование. Графика Pascal-Паскаль
Основные понятия графики
В современных компьютерах изображения на экране строятся в виде растров, и всегда прямоугольных.
Пример растра и изображения, построенного на нем:
На рисунке вы видите сильно увеличенную картинку, на самом же деле элементарные точки, из которых состоит изображение, или пиксели, должны быть очень маленькими, чтобы глаз воспринимал картинку как единое целое. Пиксель ( Pixel ) – сокращение от Picture Element (элемент рисунка).
Экраны цветных мониторов состоят из прямоугольной решетки точек (пикселей), светящихся разным цветом. Каждый цветной пиксель образован тремя более мелкими по площади участками красного, зеленого и синего цветов. При свечении этих участков с разной интенсивностью цвета смешиваются, создавая элементы изображения различных оттенков и яркости.
Важной характеристикой растра является его расширение, т.е. количество точек (пикселей) на единицу длины. Чем это число выше, тем более мелкими являются сами пиксели, и, соответственно, более плотно они располагаются на плоскости, что и приводит к тому, что мы воспринимаем их как единое, цельное изображение. Из года в год разрешающая способность мониторов, принтеров, сканеров и т.п. растет.
В современных SVGA мониторах предусмотрено, как правило, по 2 6=64 уровня интенсивности каждого из основных цветов, таким образом, в целом можно получить (2 6) 3=262144 цвета. Для представления большего числа цветов необходим больший объем памяти. Один бит может кодировать два цвета: 1 – белый, 0 – черный. Два бита могут хранить 2 2=4 цветовых комбинации, 4 бита – 16, 8 бит – 256, 16 бит – 65536, 32 бита – 4294967296.
Если для каждой точки задавать уровни красного, зеленого и синего цветов, то потребуется достаточно большой объем памяти для хранения информации об изображении. Для сокращения объема памяти используются палитры. При этом ограничиваются некоторым количеством цветов, например 16 или 256, каждому из цветов присваивается номер (соответственно, от 0 до 15 или от 0 до 255), и при записи изображения используют именно этот код. «Точка цвета номер 5». Информация о палитре, то есть данные, сколько красного, зеленого и синего нужно взять для получения «цвета номер 5», хранится и используется отдельно от записи изображения.
Важное понятие в машинной графике – графический примитив – совокупность пикселей, определяющая некоторую геометрическую фигуру. Наиболее распространенные примитивы – это точка, линия, прямоугольник, закрашенный прямоугольник, окружность и эллипс.
Растровые изображения обладают одним очень существенным недостатком: их трудно увеличивать или уменьшать, т.е. масштабировать. При уменьшении растрового изображения несколько соседних точек преобразуются в одну, поэтому теряется разборчивость мелких деталей. При увеличении – увеличивается размер каждой точки, поэтому появляется ступенчатый эффект. Кроме того растровые изображения занимают много места в памяти.
Чтобы избежать указанных проблем, изобрели так называемый векторный способ кодирования изображений.
Векторный способ представления графики заключается в том, что геометрические фигуры, кривые и прямые линии, составляющие рисунок, хранятся в памяти компьютера в виде математических формул и геометрических абстракций: круг, квадрат, эллипс и т.п. Для каждого примитива существуют свои характерные параметры. Например, для отрезка – это координаты концов; для окружности – координаты центра и радиус. Т.е. размеры, кривизна, местоположение элементов изображения хранятся в виде числовых коэффициентов. Благодаря этому появляется возможность масштабировать изображения, поворачивать, подвергать любым другим геометрическим преобразованиям с помощью простых математических операций, в частности, простым умножением параметров на коэффициент масштабирования. При этом качество изображения не меняется.
Формирование изображения на экране
Из книги Румянцева Дмитрия, Монастырского Леонида «Путь программиста: Опыт созидания личности программиста». – М.: «Издательский Дом ИНФРА-М», 2000.
Программисту не обязательно знать технические подробности конструкции монитора, но общее представление о его схеме он иметь должен. Еще важнее представлять, как программа работает с памятью, когда осуществляет вывод информации на какое-либо из устройств визуального отображения, подключенных к компьютеру.
Участок оперативной памяти компьютера, где хранится информация об изображении, появляющемся на экране, называется видеопамятью. Иногда эту область называют видеобуфером. Видеопамять занимает определенную область в адресном пространстве оперативной памяти компьютера, следовательно, видеопамять имеет ограниченный размер.
Видеопамять, как и любая другая память, соединена с процессором шиной данных. Но видеопамять, кроме того, подключена к специальной электронной схеме, которая на основе данных, хранящихся в видеобуфере, формирует изображение на экране. Физически экранное изображение обновляется 60 раз в секунду – с такой частотой упомянутая электронная схема осуществляет сканирование видеобуфера. Поэтому любое изменение состояния видеобуфера практически мгновенно (с точки зрения человека, смотрящего на экран) приводит к изменению изображения на экране.
Электронная схема, сканирующая видеобуфер и преобразующая двоичные числа в видеосигнал, называется адаптером видеодисплея или просто видеоадаптером.
Сегодня все большую популярность приобретают так называемые жидкокристаллические мониторы. Но большинство действующих сегодня мониторов по-прежнему представляют собой устройства, изображения в которых строится с помощью электронно-лучевой трубки. Напомним еще раз известный из курса физики принцип формирования изображения, получаемого в этом случае.
Этот способ называется растровым сканированием. Изображение «рисуется» тщательно сфокусированным электронным лучом. Поток электронов «бомбардирует» экран, покрытый специальным светящимся веществом – люминофором. Места, в которые ударяются электроны, начинают фосфоресцировать. В каждой точке свечение затухает приблизительно в течение нескольких сотых долей секунды, поэтому необходимо постоянно повторять «бомбардировку» поверхности экрана. Это задача специального устройства – электронной пушки. Наводчик электронной пушки (специальное электронное устройство) рассматривает весь экран как последовательность множества линий. Он «простреливает» последовательно каждую линию – слева направо, точка за точкой.
Движение луча по экрану происходит с огромной скоростью. Чтобы изображение, которое воспринимает человек, не было мерцающим, весь цикл – от первой до последней строки – должен быть закончен за 1/60 секунды (или еще быстрее). Следовательно, за секунду происходит не менее 60 проходов луча по всему экрану, строка за строкой. Такая схема формирования изображения называется растром. После того, как луч доходит до последней точки последней строки (до правого нижнего угла экрана), он мгновенно по диагонали переносится в начало первой строки экрана (левый верхний угол), и процесс повторяется.
Формирование цветного изображения осуществляется не одним, а тремя электронными лучами (красным, зеленым и синим), перемещающимся по экрану одновременно. Три луча подсвечивают сразу три элемента экрана, расположенных на очень незначительном угловом расстоянии друг от друга, поэтому человеческий глаз воспринимает эти три элемента как одну точку. Благодаря различной интенсивности свечения каждой из трех точек и эффекту аддитивного смешения трех цветов такая составная точка может иметь любой цветовой оттенок. Качество изображения тем выше, чем меньше расстояние между двумя отдельными точками. В современных мониторах расстояние между точками не превышает 0.25–0.26 мм.
Существует два принципиально разных способа указания интенсивности свечения пикселя.
Первый применяется в так называемых цифровых мониторах. В этом случае для каждой точки монитору подается информация об ее интенсивности в виде двоичного числа. Используя аддитивную модель, передавая два бита для каждого цвета (красный, зеленый и синий), из которых формируется цвет точки, можно получить 64 цвета (4*4*4). Однако при увеличении количества цветов нужно увеличивать и количество битов для каждого цвета (т.е. количество проводов для каждого цвета).
Поэтому конструкторы мониторов, в конце концов, отказались от цифровой схемы и пришли к аналоговой. При этой схеме сигналы V и H остаются по-прежнему цифровыми, а сигналы о трех составляющих цвета становятся аналоговыми и поступают по трем проводам. На каждом проводе поддерживается напряжение от 0 до 1 вольта с плавным переходом из одного состояния в другое. Ноль вольт на проводе указывает на отсутствие свечения, 1 вольт – на максимальное свечение. При такой схеме каждый из трех цветов условно может принимать бесконечное число оттенков. Следовательно, таким образом можно задавать десятки миллионов цветов.
Работа с графикой в Паскале
Формирование изображения на экране
Программисту не обязательно знать технические подробности конструкции монитора, но общее представление о его схеме он иметь должен. Еще важнее представлять, как программа работает с памятью, когда осуществляет вывод информации на какое-либо из устройств визуального отображения, подключенных к компьютеру.
Участок оперативной памяти компьютера, где хранится информация об изображении, появляющемся на экране, называется видеопамятью. Иногда эту область называют видеобуфером. Видеопамять занимает определенную область в адресном пространстве оперативной памяти компьютера, следовательно, видеопамять имеет ограниченный размер.
Видеопамять, как и любая другая память, соединена с процессором шиной данных. Но видеопамять, кроме того, подключена к специальной электронной схеме, которая на основе данных, хранящихся в видеобуфере, формирует изображение на экране. Физически экранное изображение обновляется 60 раз в секунду – с такой частотой упомянутая электронная схема осуществляет сканирование видеобуфера. Поэтому любое изменение состояния видеобуфера практически мгновенно (с точки зрения человека, смотрящего на экран) приводит к изменению изображения на экране.
Электронная схема, сканирующая видеобуфер и преобразующая двоичные числа в видеосигнал, называется адаптером видеодисплея или просто видеоадаптером.
Сегодня все большую популярность приобретают так называемые жидкокристаллические мониторы. Но большинство действующих сегодня мониторов по-прежнему представляют собой устройства, изображения в которых строится с помощью электронно-лучевой трубки. Напомним еще раз известный из курса физики принцип формирования изображения, получаемого в этом случае.
Этот способ называется растровым сканированием. Изображение «рисуется» тщательно сфокусированным электронным лучом. Поток электронов «бомбардирует» экран, покрытый специальным светящимся веществом – люминофором. Места, в которые ударяются электроны, начинают фосфоресцировать. В каждой точке свечение затухает приблизительно в течение нескольких сотых долей секунды, поэтому необходимо постоянно повторять «бомбардировку» поверхности экрана. Это задача специального устройства – электронной пушки. Наводчик электронной пушки (специальное электронное устройство) рассматривает весь экран как последовательность множества линий. Он «простреливает» последовательно каждую линию – слева направо, точка за точкой.
Движение луча по экрану происходит с огромной скоростью. Чтобы изображение, которое воспринимает человек, не было мерцающим, весь цикл – от первой до последней строки – должен быть закончен за 1/60 секунды (или еще быстрее). Следовательно, за секунду происходит не менее 60 проходов луча по всему экрану, строка за строкой. Такая схема формирования изображения называется растром. После того, как луч доходит до последней точки последней строки (до правого нижнего угла экрана), он мгновенно по диагонали переносится в начало первой строки экрана (левый верхний угол), и процесс повторяется.
Формирование цветного изображения осуществляется не одним, а тремя электронными лучами (красным, зеленым и синим), перемещающимся по экрану одновременно. Три луча подсвечивают сразу три элемента экрана, расположенных на очень незначительном угловом расстоянии друг от друга, поэтому человеческий глаз воспринимает эти три элемента как одну точку. Благодаря различной интенсивности свечения каждой из трех точек и эффекту аддитивного смешения трех цветов такая составная точка может иметь любой цветовой оттенок. Качество изображения тем выше, чем меньше расстояние между двумя отдельными точками. В современных мониторах расстояние между точками не превышает 0.25–0.26 мм.
Существует два принципиально разных способа указания интенсивности свечения пикселя.
Первый применяется в так называемых цифровых мониторах. В этом случае для каждой точки монитору подается информация об ее интенсивности в виде двоичного числа. Используя аддитивную модель, передавая два бита для каждого цвета (красный, зеленый и синий), из которых формируется цвет точки, можно получить 64 цвета (4*4*4). Однако при увеличении количества цветов нужно увеличивать и количество битов для каждого цвета (т.е. количество проводов для каждого цвета).
Поэтому конструкторы мониторов, в конце концов, отказались от цифровой схемы и пришли к аналоговой. При этой схеме сигналы V и H остаются по-прежнему цифровыми, а сигналы о трех составляющих цвета становятся аналоговыми и поступают по трем проводам. На каждом проводе поддерживается напряжение от 0 до 1 вольта с плавным переходом из одного состояния в другое. Ноль вольт на проводе указывает на отсутствие свечения, 1 вольт – на максимальное свечение. При такой схеме каждый из трех цветов условно может принимать бесконечное число оттенков. Следовательно, таким образом можно задавать десятки миллионов цветов.
Графические возможности конкретного адаптера определяются разрешением экрана, т.е. общим количеством пикселей, а также количеством цветов. Кроме того, многие адаптеры могут работать с несколькими графическими страницами.
Для инициализации графического режима используется процедура:
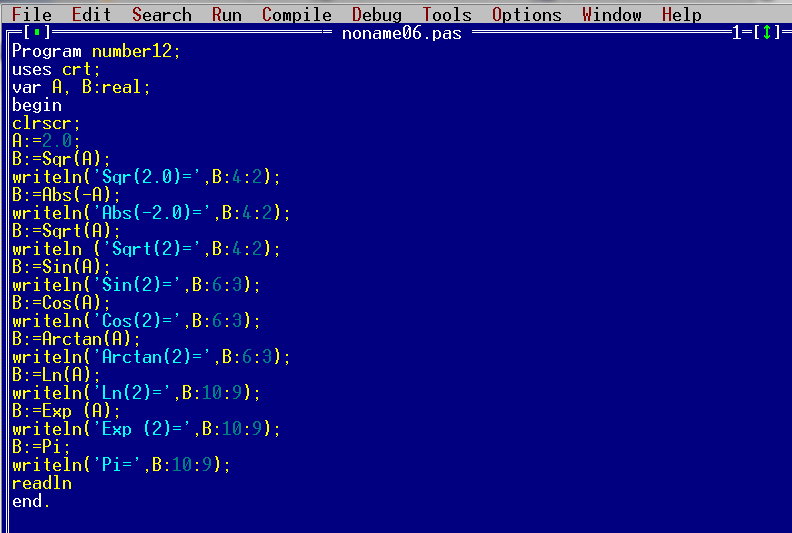
Как записать квадрат в паскале
Мы уже знаем, какие существуют функции для целых переменных. Это – нахождение модуля числа (Функция Abc), а также возведение числа в квадрат (Функция Sqr). В этом уроке мы рассмотрим функции, применяемые к дробным числам. Это функции Sqr — квадрат числа, Abs — модуль числа, Sqrt — корень числа, а также известные всем математические функции Sin, Cos, Arctan, Ln, Exp, Pi.
В строке №7 записывается функция Sqr. Это функция возведения числа в квадрат.
В строке №9 записывается операция нахождения модуля числа.
Функции Sqr и Abs мы разбирали в уроке Abs, Sqr в Pascal.
В строке №11 записывается функция Sqrt. Данная функция подсчитывает корень числа, стоящего в скобках после слова Sqrt. В нашем случае функция Sqrt будет считать корень из числа «2».
В строке №13 записываем функцию Sin. Данная функция будет подсчитывать синус числа, стоящего в скобках после записи функции.
Строка №15. Функция Cos подсчитывает косинус числа, стоящего в скобках после функции.
Строка №17. Функция Arctan вычисляет арктангенс числа, стоящего в скобках после записи функции.
Строка №19. Функция Ln подсчитывает логарифм числа, стоящего в скобках после записи функции.
Строка №21. Функция Exp возводит число «e» (экспонента — 2.72. ) в степень, значение которой указывается в скобках после слова Exp. Т.е. в нашем случае число «e» будет возведено в степень «2».
Строка №23. Переменной «B» будет присвоено значение числа «?».
Дополнение к материалу.
В прошлом уроке мы рассматривали операторы сложения, вычитания, умножения и деления. Сегодня я предлагаю рассмотреть операторы квадрата, корня и модуля.
1. Оператор квадрата
Этот оператор возводит в квадрат заданное ему число или переменную. Обозначается, как «sqr» без кавычек. В программе пишется как sqr(a), где a — любая другая переменная или число.
Данный оператор переводит число из обычного в число по модулю, то есть меняет его знак всегда на положительный. Обозначается, как «abs» без кавычек, в программе пишется, как abs(a), где a — любое число или другая переменная.
На сегодня урок окончен, с другими уроками вы можете познакомиться в категории «Уроки паскаль»
Математические операции в паскале – Pascal Математические функции для работы с числами
- Browse: Home / Самоучитель паскаль онлайн / Математические операции в паскале – Pascal Математические функции для работы с числами
Арифметические операции
Другие операции с числами
В паскале предусмотрены и многие другие операции с числами. Давайте разберем самые популярные из них.
Результат : переменной «а» присваивается значение 25.
Результат : переменной «а» присваивается значение 5.
Результат : переменной «а» присваивается значение 25.
Результат : переменной «а» присваивается значение 0.2.
Чтобы получить модуль некоторого числа используется операция abs(x).
Пример :
Результат : переменной «а» присваивается значение 8.
Это были самые важные и часто используемые операции в паскале для работы с числами ( переменными ). Найти другие вы можете на этой странице.
Выводы :
Этот раздел содержит описание математических операций, которыми можно пользоваться в выражениях на языке Паскаль. Вывести результат вычисления выражения можно такой нехитрой программе:
Конечно, результат вычисления выражения можно и записать в переменную для дальнейшего использования, и передать в другую функцию.
Не все операции и действия в этом разделе будут вам понятны. Ничего страшного — просто помните, что сюда можно вернуться, когда вам что-то понадобится.
Математические операции
В Паскале, как и в большинстве языков программирования, несколько специфически передаются основные математические операции — так математические выражения надо записывать в одну строку, а не в несколько уровней, как принято в классической математической нотации. Это достигается значительно более массовым использованием скобок, что иногда огорчает начинающих. Также всегда нужно писать знак умножения *. Кроме того, параметры функций всегда должны быть в скобках. Например:
| Математическое выражение | Запись на языке Паскаль |
| 2+2=4 | 2+2=4 |
 | a*(1+sqr(e))/2 |
 | (-b+sqrt(sqr(b)-4*a*c))/(2*a) |
 | exp(2*x+y) |
 | abs(cos(x)*sin(x)*cos(y)/tan(y)) |
если компилятор не поддерживает Tan.
Базовая арифметика
| Название операции | Оператор | Пример | Примечание |
| Добавление | + | 2+2 (=4) | |
| Вычитание | — | 18.3-11 (=7.3) | |
| Умножение | * | 7*8 (=56) | |
| Деление | / | 7/8 (=0.875) | Результат всегда действительного типа (real) |
| Целая часть деления | div | 7 div 2 (=3) | |
| Остаток от деления | mod | 7 mod 2 (=1) |
Сравнение
Все операции сравнения возвращают значение типа boolean, то есть могут использоваться в операторах ветвления и циклах, например
| Название операции | Оператор | Пример |
| Равно | = | 2+2=4 |
| Не равно (?) | <> | 2+2<>5 |
| Больше | > | 72>71.99 |
| Больше или Равно | >= | x*x>=0 |
| Меньше | Функции для преобразования действительных и целых чисел |
Паскаль — язык программирования со статической сильной типизацией. Это означает, что компилятор не выполняет преобразований значений между типами, которые могут привести к потере информации; в частности, если подставить в конструкцию, предусматривает целое значение, действительное число, компилятор сообщит об ошибке, даже если это число имеет целое значение. Так, как мы видели выше, 13 and 11 равна 9, но выражение 13.0 and 11 вызовет сообщение компилятора об ошибке! Чтобы избежать этого, надо явно задавать преобразования действительного числа на целое с помощью следующих функций:
| Название функции | описание | пример |
|---|---|---|
| Round(X) | Возвращает целое значение, ближайшее к X | Round(1.7)=2, Round(-3.1)=-3 |
| Int(X), Trunc(X) | Возвращает целую часть X | Int(1.8)=1, Trunc(-11.3)=-11 |
| Floor(X) | Возвращает наибольшее целое значение, не превышает X | Floor(1.7)=1, Floor(-3.1)=-4 |
| Ceil(X) | Возвращает наименьшее целое значение, не менее от X | Ceil(1.7)=2, Ceol(-3.1)=-3 |
Логические и побитовые операции
Логические операции используются для объединения нескольких логических условий в одну.
| Название операции | оператор | пример | описание |
|---|---|---|---|
| Логическое И, and, логическое умножение | and | (2+3=5) and (0>-1) | Истинное, если оба операнда истинны |
| Логическое ИЛИ, or, логическое сложение | or | (2+2=5) or (1=1) | Истинное, если хотя бы один из операндов истинный |
| Логическое исключающее ИЛИ, eXclusive or | xor | (2+2=5) xor (1=1) | Истинное, если ровно один из операндов истинный |
| Отрицание, логическое НЕ, not | not | not (2+2=5) | Истинное, если операнд ложный |
Логические операторы, применены к целым типов, могут использоваться, как побитовые. Чтобы получить результат побитовой операции, надо представить операнды в двоичной системе (так, как они представлены в компьютере), после чего применить соответствующую операцию в соответствующих разрядов, причем 1 означает true 0 — false. так,
| 13 в двоичной системе будет | 1 | 1 | 1 |
| 11 в двоичной системе будет | 1 | 1 | 1 |
| 9 в двоичной системе будет | 1 | 1 |
Кроме того, есть еще две побитовых операции сдвига:
| Название операции | оператор | пример | описание |
|---|---|---|---|
| сдвиг вправо | shr | 14 shr 2 (=3) | Сдвигает двоичные разряды первого операнда справа на второй операнд разрядов;эквивалент целой части деления на степень 2 |
| смещение слева | shl | 7 shl 3 (=56) | Сдвигает двоичные разряды первого операнда слева на второй операнд разрядов;эквивалент умножению на степень 2 |
Алгебраические функции
Cерым обозначены функции, которые не поддерживаются в Turbo Pascal
| Название функции | описание | Заменитель (для Turbo Pascal) |
|---|---|---|
| Pi | Возвращает значение числа  (+3,141592653589793238462643383279 … с точностью, определенным типом real) (+3,141592653589793238462643383279 … с точностью, определенным типом real) | |
| Abs(X) | Абсолютное значение (модуль) X | |
| Sign(X) | Знак числа X: 1, если X отрицательный, 1, если положительный 0, если X = 0 | |
| Exp(X) | Экспонента X (e X) | |
| Ln(X) | Натуральный логарифм X | |
| Log2(X) | Логарифм X по основанию 2 | Ln(X)/Ln(2) |
| Log10(X) | Логарифм X по основанию 10 | Ln(X)/Ln(10) |
| LogN(X,Y) | Логарифм Y по основанию X | Ln(Y)/Ln(X) |
| Power(X,Y) | Степень X Y | Exp(Y*Ln(X)) |
| Sqrt(X) | Корень квадратный из X | |
| Sqr(X) | квадрат X | |
| Max(X,Y) | Более из значений X и Y | |
| Min(X,Y) | Меньше из значений X и Y |
| Название функции | описание | Заменитель (для Turbo Pascal) |
|---|---|---|
| Randomize | Устанавливает начальное значение ГПВЧ равным текущему значению часов | |
| Randomize (X) | Устанавливает начальное значение ГПВЧ равным X | |
| Random | Возвращает псевдослучайное действительное число от 0 (включительно) до 1 (без включительно) | |
| Random (X) | Возвращает псевдослучайное целое число от 0 до X-1 | |
| Random (X, Y) | Возвращает псевдослучайное целое число от X до Y | X + Random (Y-X + 1) |
Функции для работы со сочтеными типами
Для величин сочтеных типов (все цели, буквенный, логическое и перечни) существуют также несколько удобных стандартных функций и процедур:
| Название функции | описание |
|---|---|
| Succ (X) | Возвращает значение, идет после X (для целых — X + 1, для буквенного — символ с последующим значением, для перечисления — следующее значение: так, Succ ( ‘A’) возвращает ‘B’ |
| Pred (X) | Возвращает, предшествующий X (для целых — X-1, для буквенного — символ с предыдущим значением, для перечисления — предварительное значение: так, Pred ( ‘A’) возвращает ‘@’ |
| Inc (X) | Увеличивает значение X на 1, эквивалент X = Succ (X) |
| Inc (X, N) | Увеличивает значение X на N, эквивалент N приложений Inc (X) |
| Dec (X) | Уменьшает значение X на 1, эквивалент X = Pred (X) |
| Dec (X, N) | Уменьшает значение X на N, эквивалент N применений Dec (X) |
| Ord (X) | Возвращает X (для нечисловых типов) |
| Odd (X) | Проверяет X на нечетность, true, если X нечетный или false, если X имеет четное значение |
Приоритет операций
Во время разбора математического выражения Паскаль сначала выполняет операции с высоким приоритетом, затем с низким, все справа налево. Так, в выражении 2 + 2 * 2 сначала будет вычислено 2 * 2 = 4, а уже затем 2 + 4 = 6 — так же, как в обычной математике; в выражении 10 mod 2 * 3 сначала будет выполнено 10 mod 2 = 0, а уже потом 0 * 3 = 0!
Теперь вы знаете какие однокоренные слова подходят к слову Как написать квадрат в паскале, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову "Как написать квадрат в паскале", предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором.