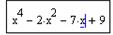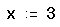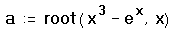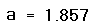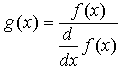Слово Как написать корень в маткаде - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Как поставить корень в mathcad

Как поставить корень в маткаде

1. Построить график функции f(x).Отделить все корни, лежащие на данном отрезке.

2. Вычислить наибольший из корней методами, указанными в варианте. Точность . Программа должна быть универсальной. Методы оформить в виде отдельных подпрограмм, содержащих проверку условий сходимости метода. Метод, начальное приближение задавать как параметр, вводимый с клавиатуры. Вычислить корень при различных значениях . Вывод на консоль: метод, , номер итерации — k, , .

3. Сравнить число необходимых итераций в обоих методах, указать преимущества и недостатки методов. Сделать выводы.

4. Графически проиллюстрировать сходимость методов для своего уравнения.

5. Вычислить наибольший из корней в MathCAD.

Из графика видно, что первый корень находится на отрезке [-2;-1], второй на отрезке [1;3], а третий- [3;5]. Наибольший корень лежит на отрезке [3;5].

Составим программу для вычисления наибольшего из корней данного уравнения:

РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ

4 Решение уравнений и систем средствами Mathcad

Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.

Функция root, блоки Given…Find, Given…Minerr

В ходе численного решения обычно выделяют два этапа:

Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается

root(f(x), x, [a, b])

и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:

Этот прием используется в Mathcad так:

Кроме того, пакет Mathcad имеет встроенную функцию

lsolve(A, b),

Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.

Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.

Порядок выполнения лабораторной работы

Лабораторная работа № 4
Решение уравнений и систем в Mathcad.

Решение.

Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.

Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:

Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:

Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).

Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).

Для появления графика щелкнем левой клавишей мыши вне графической области.

Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.

Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.

После указанных преобразований график функции f(x) будет выглядеть следующим образом:

Этап отделения корней завершен.

Уточним теперь корни уравнения с помощью функции root.

Присвоим начальное приближение переменной x и укажем точность поиска корня:

Уточним заданное приближение к значению корня с помощью функции root:

Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:

Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:

Решение.

Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:

Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.

Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.

Для получения результата напечатаем polyroots(v) =:

Задание 3. Решить систему линейных уравнений Сделать проверку.

Решение.

1-й способ. Использование блока Given … Find.

Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:

Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).

После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:

Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом

После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.

2-й способ. Использование блока Given…Minerr.

Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:

3-й способ. Решение системы линейных уравнений матричным способом.

Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:

Решим систему матричным способом по формуле

Решим систему с помощью функции lsolve:

Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:

Автор Механик задал вопрос в разделе Другие языки и технологии

Ответ от Chiquitita Preciosa[гуру]
Корень—обратный слэш

Как поставить корень в mathcad

Иллюстрированный самоучитель по MathCAD 12

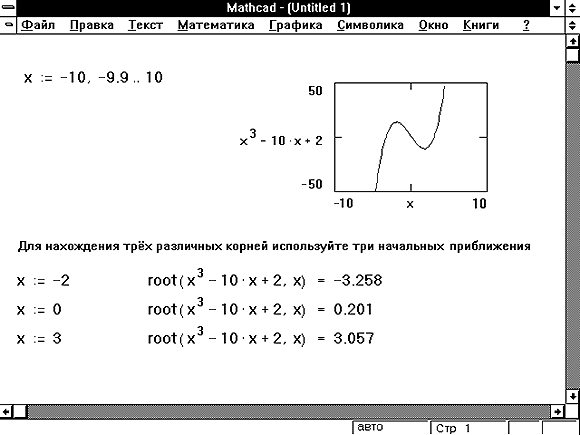
Чтобы решить задачу предварительной (грубой) локализации корней, в самых простых случаях можно использовать графическое представление f (х) (см. рис. 5.1, 5.2 и 5.4). Понятно, что в случае многомерных систем такой способ практически неприменим. Если требуется исследовать определенную область определения переменных уравнения на наличие корней, определив их примерное положение, то обычно применяют весьма расточительный способ, называемый сканированием. Оно состоит в последовательном поиске корня, начиная из множества пробных точек, покрывающих расчетную область.

Обычно (вне Mathcad) сканирование организуют следующим образом. Область определения функции разбивается на элементарные области (в случае функции двух переменных чаще всего прямоугольные, в случае трех переменных – кубические и т. д.). Из центра каждой элементарной области запускается численный метод поиска корня, и в случае выхода итераций за ее пределы расчеты прерываются, а в противном случае происходит нахождение корня.

Гораздо менее надежной (но зато более экономной) альтернативой является простое вычисление и сравнение между собой невязок системы уравнений в центральных точках элементарных областей. На тех участках области определения, где норма невязки невелика, вероятность локализации корня больше, и именно из локальных минимумов нормы невязки можно запускать градиентный метод для уточнения корня.

Пример организации упрощенного варианта сканирования по одной переменной приведен на рис. 5.6. График функции, корни которой подлежат определению, показан в его верхней части. Затем осуществляется решение уравнения при помощи функции root, для нескольких последовательно расположенных узлов. Результат выдается в последней строке листинга в виде таблицы, из которой видно, что на рассматриваемом интервале уравнение имеет три корня.

Примечание
Конечно, гарантии, что все существующие корни будут найдены, особенно в многомерных случаях, чаще всего нет. Всегда существует вероятность «просмотреть» корень, расположенный между узлами сканирования.

Источник

Как написать корень в маткаде

Как описано в предшествующем разделе, Mathcad воспринимает комплексные числа в форме a + bi, где a и b — обычные числа. Можно использовать букву j вместо i, если это удобнее.

Комплексные числа могут также возникать в результате вычислений, даже если все исходные значения вещественны. Например, если вычислить 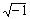, Mathcad вернёт i.

Хотя можно вводить мнимые числа, сопровождая их i или j, Mathcad обычно отображает их сопровождаемыми i. Чтобы Mathcad показывал мнимые числа с j, выберите Формат числа из меню Математика, нажмите на кнопку “Глобальный” и переключите “Мн. ед”. на j.

При вводе комплексных чисел не забудьте, что нельзя использовать i или j сами по себе для ввода комплексной единицы. Нужно всегда печатать 1i или 1j, в противном случае Mathcad истолкует i или j как переменную. Когда курсор покидает выражение, содержащее 1i или 1j, Mathcad скрывает избыточную 1.

Специальные операции над комплексными числами

В Mathcad есть следующие специальные функции и операторы для работы с комплексными числами:

Рисунок 2 показывает некоторые примеры использования комплексных чисел в Mathcad.

Рисунок 2: Комплексные числа в Mathcad.

При использовании в комплексной области многие функции, о которых мы привыкли думать как о возвращающих одно значение, становятся многозначными.

Общее правило состоит в том, что для многозначной функции Mathcad всегда возвращает значение, составляющее на комплексной плоскости самый маленький положительный угол с положительным направлением действительной оси. Оно называется главным значением.

Единственное исключение из этого правила — оператор n-ого корня, описанный в главе Список операторов. Этот оператор возвращает вещественный корень всякий раз, когда это возможно. Рисунок 3 показывает эту особенность.

Рисунок 3: Нахождение вещественных корней n—ой степени из отрицательного числа.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Как написать корень в маткаде

Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.

root( f(z), z)

Возвращает значение z, при котором выражение или функция f(z) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр.

Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.

Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.

Функция root предназначена для решения одного уравнения с одним неизвестным. Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.

Рисунок 1: Использование графика и функции root для поиска корней уравнения.

Что делать, когда функция root не сходится

Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.

Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find

Некоторые советы по использованию функции root

Решение уравнений с параметром

Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции

Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.

Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.

Рисунок 2: Определение функции пользователя с функцией root.

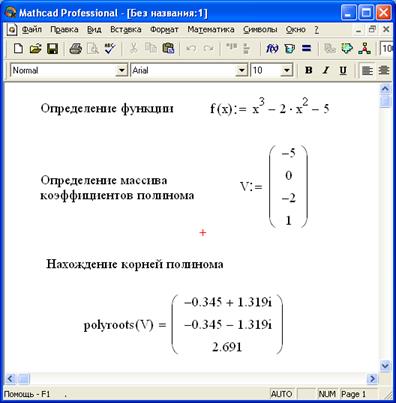
Нахождение корней полинома

Для нахождения корней выражения, имеющего вид

лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.

Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.

Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.

Рисунок 4: Использование функции polyroots для поиска корней полинома.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Функция polyroots в mathcad

Для нахождения корней полинома в MathCAD предназначена специальная функция polyroots (v). Она находит как действительные, так и комплексные корни полинома n-ой степени, коэффициенты которого хранятся в массиве v длиной n+1. Параметром данной функции является вектор-столбец коэффициентов полинома v.

Пример использования функции polyroots показан на рисунке 3.1.4. При решении задачи надо правильно формировать вектор-столбец коэффициентов полинома v, записывая в него значения коэффициентов, начиная коэффициентов при х в нулевой степени.

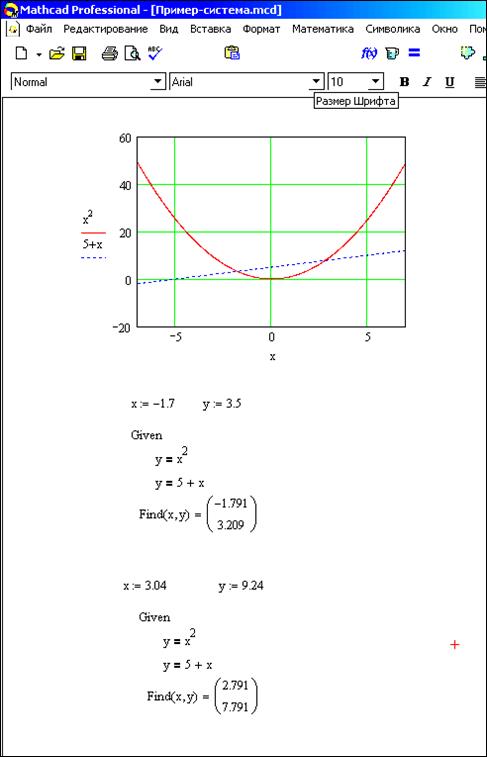
Решение систем уравнений

Системы уравнений в MathCAD решаются в следующем порядке:

1. Находится приближенное решение системы уравнений. Приближенное решение удобнее всего найти графически;

3. Записывается любое выражение, использующее функцию Find. Параметрами данной функции являются все переменные, входящие в систему. Функция возвращает вектор-столбец решений системы.

Рисунок 3.1.4 – Нахождение корней полинома при помощи функции

Пример 3.3 Найти решение системы уравнений

.

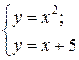
Процесс решения данной системы уравнений показан на рисунке 3.2.1

В результате функция Find вернула вектор-столбец и . Это значит, что решением системы уравнений являются значения и .

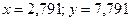
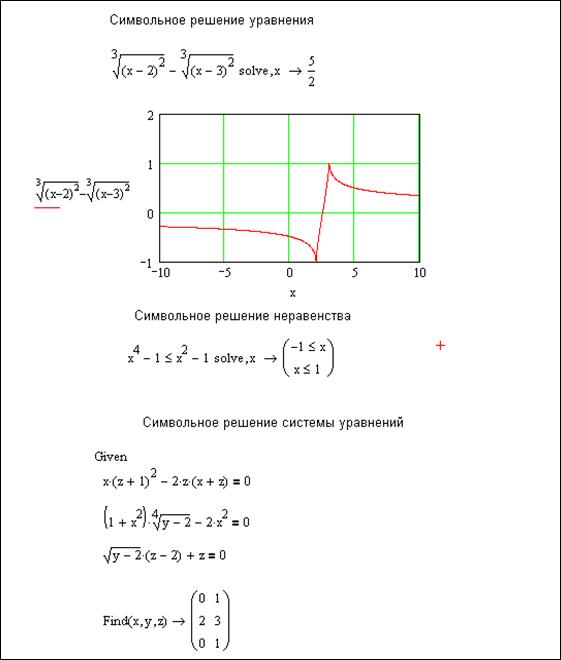
Символьное решение уравнений, неравенств и систем уравнений

Для символьного решения уравнений и неравенств надо выполнить следующее:

1. Вставить в рабочий лист структуру solve c панели инструментов Simbolic.

2. Ввести данные: слева – уравнение или неравенство, справа – переменную, относительно которой требуется его разрешить.

3. Щёлкнуть вне области решения, чтобы получить результат.

Рисунок 3.2.1 – Пример решения системы уравнений

При символьном решении уравнений и неравенств следует вводить знаки =, , находящиеся на панели инструментов Boolean.

При символьном решении системы уравнений после Find надо ввести с панели инструментов Simbolic.

Пример символьного решения уравнений, неравенств и систем уравнений показан на рисунке 3.3.1

Рисунок 3.3.1 – пример символьного решения уравнения, неравенства

и системы уравнений

Некоторые возможности MathCAD

В этом разделе приводятся краткие сведения о возможностях MathCAD, которые могут быть полезны в процессе обучения.

Комплексные числа в MathCAD

MathCAD Воспринимает комплексные числа в форме a+bi, где a и b – вещественные числа. Комплексные числа можно вводить, или получать в результате вычислений. При вводе мнимые числа заканчиваются символом i или j. Нельзя использовать i или j сами по себе для обозначения мнимой единицы, во избежание смешения с именами переменных. Для ввода мнимой единицы следует напечатать 1i или 1j. При выходе из поля ввода единица не будет отображаться. Можно использовать j вместо i, если это удобнее. Чтобы MathCAD показывал нужный вам символ (i или j), выберите «Формат числа» из меню «Математика», нажмите на кнопку «Глобальный» и переключите «Мн.ед.» на i или j.

MathCAD содержит следующие операторы и функции для работы с комплексными числами:

Re(z) – вещественная часть z.

Im(z) – мнимая часть z.

arg(z) – угол в комплексной плоскости между вещественной осью и z. Результат заключён между π и –π.

– модуль z. Чтобы записать модуль выражения, заключите его в выделяющую рамку и нажмите клавишу с вертикальной чертой «|».

При использовании в комплексной области многие функции являются многозначными. Для многозначной функции MathCAD возвращает значение, составляющее на комплексной плоскости самый малый положительный угол с положительным направлением действительной оси, то есть главное значение.

Рисунок 3.4.1 – Комплексные числа в MathCAD

На рисунке 3.4.1 показан пример использования возможностей MathCADпри работе с комплексными числами.

Последнее изменение этой страницы: 2016-12-28; Нарушение авторского права страницы

Решение уравнений с помощью функции root(f(x),x)

Способы решения уравнений в MathCAD

Форматирование трехмерных графиков

Для форматирования графика необходимо дважды щелкнуть по области построения — появится окно форматирования с несколькими вкладками: Appearance,General,Axes,Lighting,Title,Backplanes,Special, Advanced, Quick Plot Data.

Назначение вкладки Quick Plot Data было рассмотрено выше.

Вкладка Appearance позволяет менять внешний вид графика. Поле Fill Options позволяет изменить параметры заливки, поле Line Option — параметры линий, Point Options — параметры точек.

Во вкладке General (общие) в группе View можно выбрать углы поворота изображенной поверхности вокруг всех трех осей; в группе Display asможно поменять тип графика.

Во вкладке Lighting (освещение) можно управлять освещением, установив флажок Enable Lighting (включить освещение) и переключатель On(включить). Одна из 6-ти возможных схем освещения выбирается в списке Lighting scheme(схема освещения).

В данном разделе мы узнаем, каким образом в системе MathCAD решаются простейшие уравнения вида F(x) = 0. Решить уравнение аналитически — значит найти все его корни, т.е. такие числа, при подстановке которых в исходное уравнение получим верное равенство. Решить уравнение графически — значит найти точки пересечения графика функции с осью ОХ.

Для решений уравнения с одним неизвестным вида F(x) = 0 существует специальная функция

root(f(x),x),

где f(x) — выражение, равное нулю;

Эта функция возвращает с заданной точностью значение переменной, при котором выражение f(x) равно 0.

Внимание. Если правая часть уравнения ¹0, то необходимо привести его к нормальному виду (перенести все в левую часть).

Перед использованием функции rootнеобходимо задать аргументу х начальное приближение. Если корней несколько, то для отыскания каждого корня необходимо задавать свое начальное приближение.

Внимание. Перед решением желательно построить график функции, чтобы проверить, есть ли корни (пересекает ли график ось Ох), и если есть, то сколько. Начальное приближение можно выбрать по графику поближе к точке пересечения.

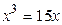
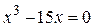
Пример. Решение уравнения с помощью функции root представлено на рисунке 3.1. Перед тем как приступить к решению в системе MathCAD, в уравнении все перенесем в левую часть. Уравнение примет вид: .

Рис. 3.1. Решение уравнения при помощи функции root

Для одновременного нахождения всех корней полинома используют функцию Polyroots(v),где v — вектор коэффициентов полинома, начиная со свободного члена.Нулевые коэффициенты опускать нельзя.В отличие от функции root функция Polyroots не требует начального приближения.

Пример. Решение уравнения 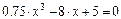с помощью функции polyroots представлено на рисунке 3.2.

Рис. 3.2. Решение уравнения с помощью функции polyroots

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась – это был конец пары: «Что-то тут концом пахнет». 8526 – | 8113 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.

root( f(z), z)

Возвращает значение z, при котором выражение или функция f(z) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр.

Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.

Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.

При использовании функции root имейте в виду следующее:

Функция root предназначена для решения одного уравнения с одним неизвестным. Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.

Рисунок 1: Использование графика и функции root для поиска корней уравнения.

Что делать, когда функция root не сходится

Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.

Если после многих итераций Mathcad не может найти подходящего приближения, то появляется сообщение об ошибке “отсутствует сходимость”. Эта ошибка может быть вызвана следующими причинами:

Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find

Некоторые советы по использованию функции root

В этом разделе приведены несколько советов по использованию функции root:

Решение уравнений с параметром

Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции

Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.

Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.

Рисунок 2: Определение функции пользователя с функцией root.

Нахождение корней полинома

Для нахождения корней выражения, имеющего вид

лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.

Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.

Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.

Рисунок 4: Использование функции polyroots для поиска корней полинома.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник