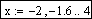Слово Как написать косинус в маткаде - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Как записать arccos в mathcad

Как записать sin в квадрате в mathcad

Система MathCAD содержит большой набор встроенных элементарных функций. Функции задаются своими именами и значениями аргумента, заключёнными в круглых скобках. Функции, как и переменные, и числа, могут входить в состав математических выражений. В ответ на обращение к ним, функции возвращают вычисленные значения. Ниже представлены некоторые из этих функций.

1.2.1 Тригонометрические функции

1.2.2 Гиперболические функции

sinh (z) — гиперболический синус
cosh(z) — гиперболический косинус
tanh(z) — гиперболический тангенс
sech(z) — гиперболический секанс
csch(z) — гиперболический косеканс
coth(z) — гиперболический котангенс

1.2.3 Обратные тригонометрические функции

asin (z) — арксинус
acos(z) — арккосинус
atan(z) — арктангенс

1.2.3 Обратные тригонометрические функции

asin (z) — арксинус
acos(z) — арккосинус
atan(z) — арктангенс

1.2.4 Обратные гиперболические функции

asinh (z) — обратный гиперболический синус
acosh(z) — обратный гиперболический косинус
atanh(z) — обратный гиперболический тангенс

1.2.5 Показательные и логарифмические функции

exp (z) — экспоненциальная функция
ln (z) — натуральный логарифм
log (z) — десятичный логарифм

1.2.6 Функции с условиями сравнения

ceil (x) — наименьшее целое, большее или равное х
floor(x) — наибольшее целое, меньшее или равное х
mod(x,y) — остаток отделения х/у со знаком х
angle(x,y) — положительный угол с осью х для точки с координатами (х,у)

Синус в квадрате X
Как собственно записать F(x)=sin^2\,x-cos\,2x Точнее сам синус в квадрате икс. Range(«B» &.

Построить график функции тангенс в квадрате
Нужно построить график функции тангенс в квадрате tan2(x). Помогите, у меня не получается. Вот мой.

Нарисовать квадрат в квадрате, в квадрате и так далее
Прошу помощи, мне подкинули задачку. Необходимо вывести на экран вот это: * * * * * * * * * *.

Найти сумму чисел 1 в квадрате до 10 в квадрате
Создать программу по всем 3 видам циклов. цикл с параметром,цикл с условием,цикл,и цикл с.

Найти сумму от N в квадрате, до 2N в квадрате
Дано N(>0) Найти сумму sqr(N)+sqr(N+1)+sqr(N+2)+. +sqr(2*N)

График, как задать синус в квадрате

Не могу построить график, пробовал вариант, заменяя выражение (выделеные) на sin(x) = sin(pi/6)(3-4t^2), все равно нечего не хочет работать. Может кто поможет или даст ссылку, где написано, как решить мою проблему, заранее спасибо.

Синус в квадрате X
Как собственно записать F(x)=sin^2\,x-cos\,2x Точнее сам синус в квадрате икс. Range(«B» &.

Построить график функции тангенс в квадрате
Нужно построить график функции тангенс в квадрате tan2(x). Помогите, у меня не получается. Вот мой.

Не работает ln^2(ln в квадрате)

Нарисовать квадрат в квадрате, в квадрате и так далее
Прошу помощи, мне подкинули задачку. Необходимо вывести на экран вот это: * * * * * * * * * *.

Найти сумму чисел 1 в квадрате до 10 в квадрате
Создать программу по всем 3 видам циклов. цикл с параметром,цикл с условием,цикл,и цикл с.

Найти сумму от N в квадрате, до 2N в квадрате
Дано N(>0) Найти сумму sqr(N)+sqr(N+1)+sqr(N+2)+. +sqr(2*N)

Х в квадрате
каким образом мжно делать что бы Х выводился на экарн со степенем?

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Синус в квадрате X
Как собственно записать F(x)=sin^2\,x-cos\,2x Точнее сам синус в квадрате икс. Range(«B» &.

Прямоугольник в квадрате
Здравствуйте,попал в очень неприятную ситуацию, понадеялся на человека, а он «не смог». Времени.

Жизнь в квадрате
В некоторых клетках квадрата N x N живут микроорганизмы (не более одного в одной клетке). Каждую.

Задача о квадрате
Есть у нас квадрат у него бросают 3 точки какая вероятность того что эти три точку образуют 1).

Источник

Как написать косинус в маткаде

Этот раздел описывает тригонометрические, гиперболические и показательные функции Mathcad вместе с обратными им. Здесь также описываются встроенные функции Бесселя.

Тригонометрические функции и обратные им.

Тригонометрические функции Mathcad и обратные им определены для любого комплексного аргумента. Они также возвращают комплексные значения везде, где необходимо. Результаты для комплексных значений вычисляются с использованием тождеств:

Для применения этих функций к каждому элементу вектора или матрицы используйте оператор векторизации.

Обратите внимание, что все эти тригонометрические функции используют аргумент, выраженный в радианах. Чтобы перейти к градусам, используется встроенная единица deg. Например, чтобы вычислить синус 45 градусов, введите sin(45*deg).

Имейте в виду, что из-за ошибок округления, свойственных машинной арифметике, Mathcad может возвращать очень большое число в той точке, где находится особенность вычисляемой функции. Вообще, необходимо быть осторожным при вычислениях в окрестности таких точек.

asin(z)	Возвращает угол (в радианах), чей синус — z.
acos(z)	Возвращает угол (в радианах), чей косинус — z.
atan(z)	Возвращает угол (в радианах), чей тангенс — z.

Гиперболические функции sinh и cosh определяются формулами:

Эти функции также могут использовать комплексный аргумент и возвращать комплексные значения. Гиперболические функции тесно связаны с тригонометрическими функциями. Справедливы формулы:

sinh(iz)=isin(z)cosh(iz)=cos(z)

sinh (z)	Возвращает гиперболический синус z.
cosh (z)	Возвращает гиперболический косинус z.
tanh (z)	Возвращает sinh(z)/cosh(z), гиперболический тангенс z.
csch (z)	Возвращает 1/sinh(z), гиперболический косеканс z.
sech (z)	Возвращает 1/cosh(z), гиперболический секанс z.
coth (z)	Возвращает 1/tanh(z), гиперболический котангенс z.
asinh (z)	Возвращает число, чей гиперболический синус — z.
acosh (z)	Возвращает число, чей гиперболический косинус — z.
atanh (z)	Возвращает число, чей гиперболический тангенс — z.

Логарифмические и показательные функции

Логарифмические и показательные функции Mathcad могут использовать комплексный аргумент и возвращать комплексные значения. Значения экспоненциальной функции для комплексного аргумента вычисляются с применением формулы

e x+iy =e x (cos(y) + isin(y))

Вообще говоря, значения натурального логарифма даются формулой

ln(x + iy)=ln|x + iy|+ atan(y/x)i + 2n p i

В Mathcad функция ln возвращает значение, соответствующее n = 0. А именно:

ln(x + iy)=ln|x + iy|+ atan(y/x)i

Оно называется основным значением логарифма. Рисунок 1 иллюстрирует некоторые основные свойства логарифма.

exp(z)	Возвращает e в степени z.
ln(z)	Возвращает натуральный логарифм z. (z0).
log(z)	Возвращает логарифм z по основанию 10. (z0).

На Рисунке 1 показано, как можно использовать эти функции для вычисления логарифма по любому основанию.

Рисунок 1: Использование логарифмических функций.

Эти функции обычно возникают как решения для волнового уравнения, подчиненного цилиндрическим граничным условиям.

Функции Бесселя первого и второго рода, J_n(x) и Y_n(x), являются решениями для дифференциального уравнения

Модифицированные функции Бесселя первого и второго рода, I_n(x) и K_n(x), являются решениями для немного видоизмененного уравнения:

J0(x)	Возвращает J0(x); x вещественный.
J1(x)	Возвращает J1(x); x вещественный.
Jn(m, x)	Возвращает Jn(x); x вещественный, 0m100.
Y0(x)	Возвращает Y0(x); x вещественный, x > 0.
Y1(x)	Возвращает Y1(x); x вещественный, x > 0.
Yn(m, x)	Возвращает Yn(x). x > 0, 0m100
I0(x)	Возвращает I0(x); x вещественный.
I1(x)	Возвращает I1(x); x вещественный.
In(m, x)	Возвращает In(x); x вещественный, 0m100.
K0(x)	Возвращает K0(x); x вещественный, x > 0.
K1(x)	Возвращает K1(x); x вещественный, x > 0.
Kn(m, x)	Возвращает Kn(x). x > 0, 0m100

Следующие функции возникают в широком круге задач.

x должен быть вещественным. G (z) Возвращает значение эйлеровой гамма-функции в z. Для вещественного z значения этой функции совпадают со следующим интегралом:

Гамма-функция Эйлера удовлетворяет рекуррентному соотношению

Откуда следует для положительных целых z:

Интеграл ошибок часто возникает в статистике. Он может также быть использован для определения дополнения интеграла ошибок по формуле:

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Встроенные операторы и функции Mathcad

Таблица ПЗ.1. Арифметические операторы

Вычитание или отрицание (унарная операция)

Матричное умножение, умножение на скаляр

Скобки (изменение приоритета)

Возведение в степень n

Возведение матрицы в степень n

Скалярные операции над векторами и матрицами, если это не оговорено особо, производятся независимо над их каждым элементом, как над скаляром.

Таблица П3.2. Вычислительные операторы

Вычисление n-й производной

Сумма ранжированной переменной

Произведение ранжированной переменной

Таблица ПЗ.З. Встроенные функции по алфавиту

Обратная тригонометрическая или гиперболическая функция *

Функция Эйри первого рода

х,у — координаты точки

Угол между точкой и осью ОХ

file— строковое представление пути к файлу

Дозапись данных в существующий текстовый файл

z — аргумент функции

Аргумент комплексного числа

х,у — координаты точки

Угол, отсчитываемый от оси ОХ до точки (х,у)

А,В,С. — векторы или матрицы

Слияние матриц слева направо

n — порядок х — аргумент

Мнимая и действительная части функции Бесселя —Кельвина

Функция Эйри второго рода

х,у — векторы данных

и — вектор значений сшивок В-сплайнов

n — порядок полиномов

Вектор коэффициентов В-сплайна

Bulstoer (y0, t0, t1, M, D)

Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера

bulstoer (y0, t0, t1, acc, D, k, s)

Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера (для определения только последней точки интервала)

Bvalf it (z1, z2, x0, x1, xf, D, load1, load2, score)

zl,z2 — вектор начальных значений для недостающих левых и правых граничных условий

хО — левая граница xl — правая граница xf — внутренняя точка

D(x,y) — векторная функция, задающая систему ОДУ

Возвращает вектор недостающих граничных условий у краевой задачи для системы N ОДУ с дополнительным условием в промежуточной точке

Наименьшее целое, не меньшее х

Вектор прямого комплексного преобразования Фурье (в разных нормировках)

А — квадратная, определенная матрица

А — матрица или вектор

Объединение строковых переменных

А — квадратная матрица

Числа обусловленности в разных нормах (Ы, L2, Евклидова, »)

А — матрица i — индекс столбца

Сортировка строк матрицы по элементам 1-го столбца

CreateMesh (F, s0, s1, t0, t1, sgr, tgr, fmap)

tO.tl — пределы! sO.sl — пределы s

tgr, sgr — число точек сетки по t и s

fmap— функция преобразования координат

Cre-ateSpace(F[, t0, t1, tgr, fmap])

F(t) — векторная функция из трех элементов

tgr — число точек сетки по t

fmap— функция преобразования координат

Комплексный знак числа

х,у — векторы данных

Вектор коэффициентов кубического сплайна

r,6,z— цилиндрические координаты

Преобразование цилиндрических координат в прямоугольные

х— значение случайной величины

par — список параметров распределения *

Плотность вероятности со статистикой распределения *

Диагональная матрица, на диагонали которой находятся элементы вектора

А — квадратная матрица

Собственные значения матрицы

А — квадратная матрица

А. — собственное значение

Собственный вектор матрицы, соответствующий заданному собственному значению

А — квадратная матрица

Собственные векторы матрицы

Обратная функция ошибок

Возвращает строку S как сообщение об ошибке

Экспонента в степени z

x,y — векторы данных

g — вектор начальных значений а,Ь,с

Вектор прямого преобразования Фурье (в разных нормировках)

Функция Бесселя второго рода нулевого, первого и m-го порядка

n — порядок х — аргумент

Сферическая функция Бесселя второго рода

Некоторые функции, составляющие семейства типовых функций, приведены в сокращенном виде с недостающей частью имени в виде звездочки *. Например, различные статистические функции, описывающие различные распределения, или функции вывода в файлы. Подробные сведения содержатся в разделе, на который указывает соответствующая ссылка.

Источник

Как написать косинус в маткаде

БАЗОВЫЕ ОПЕРАЦИИ.
РАНЖИРОВАННЫЕ ПЕРЕМЕННЫЕ. ФУНКЦИИ. ГРАФИКИ
МАССИВЫ

1 Запуск. Формульные и текстовые области

Запуск Mathcad: Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).

Документ Mathcad просматривается, интерпретируется и выполняется слева направо и сверху вниз и может включать три вида областей:

Для ввода математических символов: View / Toolbars / Math (Вид / Панели инструментов / Математическая).

Каждое математическое выражение набирается в отдельной формульной области. Одна формула – одна область!

Для вставки в документ текстовой области выполняют Insert / Text Region (Вставка / Область текста), либо просто нажимают в формульной области Пробел. Текстовая область имеет рамку с маркерами, позволяющими изменять ее размеры, и курсор в виде вертикальной линии красного цвета.

2 Ранжированные переменные. Функции. Графики

В Mathcad существует тип переменных, принимающих не одно, а множество значений. Такие переменные носят название ранжированных или дискретных. Ранжированная переменная – переменная, которая принимает ряд значений при каждом ее использовании, причем каждое значение отличается от соседнего на постоянную величину, называемую шагом.

Ранжированная переменная общего вида определяется выражением:

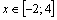
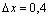
Например, если переменная изменяется в интервале с шагом , то она задается в виде

Шаг изменения значений ранжированной переменной в явном виде обычно не задается, он определяется как x2 – x1.

Функции в системе Mathcad можно условно разделить на две группы: встроенные и функции пользователя. Встроенные функции изначально заданы в системе разработчиками. Имя функции вводится с клавиатуры, обычно в нижнем регистре. Полный перечень встроенных функций можно получить, выполнив команду Function (Функция) главного меню Insert (Вставка), или нажав на кнопку панели инструментов. При этом появляется окно, где справа перечислены возможные категории функций, а слева – список функций из выделенной категории.

Среди наиболее часто используемых функций можно указать:

Функция пользователя сначала должна быть определена, а затем к ней можно обращаться при вычислениях, записи алгебраических выражений, построении графиков и т. п. Функция пользователя определяется

Имя(список аргументов) := Выражение

Сначала задается имя функции, в круглых скобках указывается список аргументов функции (перечень используемых переменных), разделяемых запятыми. Затем вводится оператор присваивания. Справа от него записывается выражение, содержащее доступные системе операторы, операнды и функции с аргументами, указанными в списке аргументов.

Обращение к функции осуществляется по ее имени с подстановкой на место аргументов констант, переменных, определенных до обращения к функции, и выражений.

Основные виды графиков и инструменты для работы с ними находятся на палитре математических инструментов Graph (График).

Для построения графика функции одной переменной в декартовой системе координат в Mathcad:

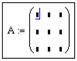
Массив в пакете Mathcad – это совокупность конечного числа упорядоченных пронумерованных элементов, которая может иметь уникальное имя. Обычно используют одномерные (векторы) и двумерные (матрицы) массивы, содержащие числовые, символьные или строковые данные.

– вектор-столбец; – вектор-строка.

Порядковый номер элемента называется индексом. Местоположение элемента в массиве задается одним индексом для вектора и двумя – для матрицы. Номер первого элемента массива определяется значением системной переменной ORIGIN. По умолчанию ORIGIN = 0 и может принимать только целые значения. Изменение значения этой системной переменной осуществляется последовательностью команд Math / Options… / Built-In Variables / Array Origin (ORIGIN) (Математика / Параметры / Встроенные переменные / Начальный индекс массивов) или переопределением в документе, например:

Существует несколько способов создания массивов.

1-й способ. Использование панели Matrix (Матрицы).

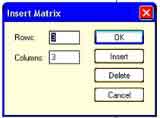
Сначала набирается имя массива и оператор присваивания, например, . Далее на панели Math (Математика) выбираем кнопку Matrix (Матриц):

Далее указываем количество ее строк m (Rows) и столбцов n (Columns) матрицы. Для векторов один из этих параметров должен быть равен 1. При m = 1 получим вектор-строку, а при n = 1 – вектор-столбец.

На месте курсора появится шаблон, в знакоместа которого вводятся значения элементов массива:

2-й способ. Использование ранжированной переменной.

Целочисленные ранжированные переменные используются для задания индексов и позволяют создавать массивы в следующем порядке:

Обращаться к отдельным элементам вектора или матрицы можно, используя нижний индекс, принимающий только целочисленные значения. Для ввода нижнего индекса после имени вектора или матрицы нажимается клавиша «[» (прямая открывающая скобка) либо используется пиктограмма с палитры математических инструментов Matrix. Для элемента матрицы указываются через запятую два индекса, обозначающих номер строки и номер столбца соответственно.

Для работы с векторами и матрицами система Mathcad имеет ряд специальных операторов и команд (представленных в таблице 1), используя которые не следует забывать об общих правилах матричного исчисления.

Таблица 1 – Команды палитры инструментов Matrix (Матрица)

Источник