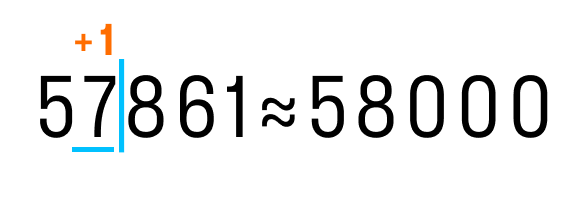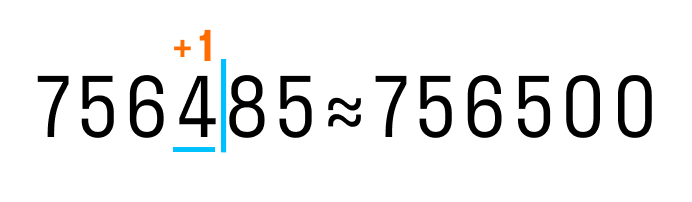Правильное округление чисел
Приближенные значения
В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.
У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Примерчики
Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.
Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.
Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.
Приближенное значение — число, которое получилось после округления.
Для записи результата округления используют знак «приблизительно равно» — ≈.
Округлить можно любое число — для всех чисел работают одни и те же правила.
Округлить число значит сократить его значение до нужного разряда, например, до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.
Округление натуральных чисел
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.
Особенности натуральных чисел:
Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.
Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.
Правила округления чисел:
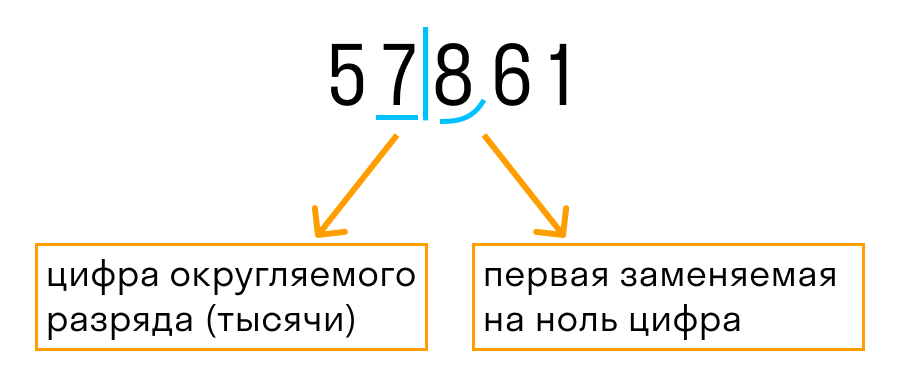
Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.
После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.
Теперь округлим 756 485 до сотен:
Округлим число 123 до десятков: 123 ≈ 120.
Округлим число 3581 до сотен: 3581 ≈ 3580.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.
Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:
Округление десятичных дробей
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Есть два формата записи:
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10 000 и т. д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:
Разряды целой части:
Разряды дробной части:
Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.
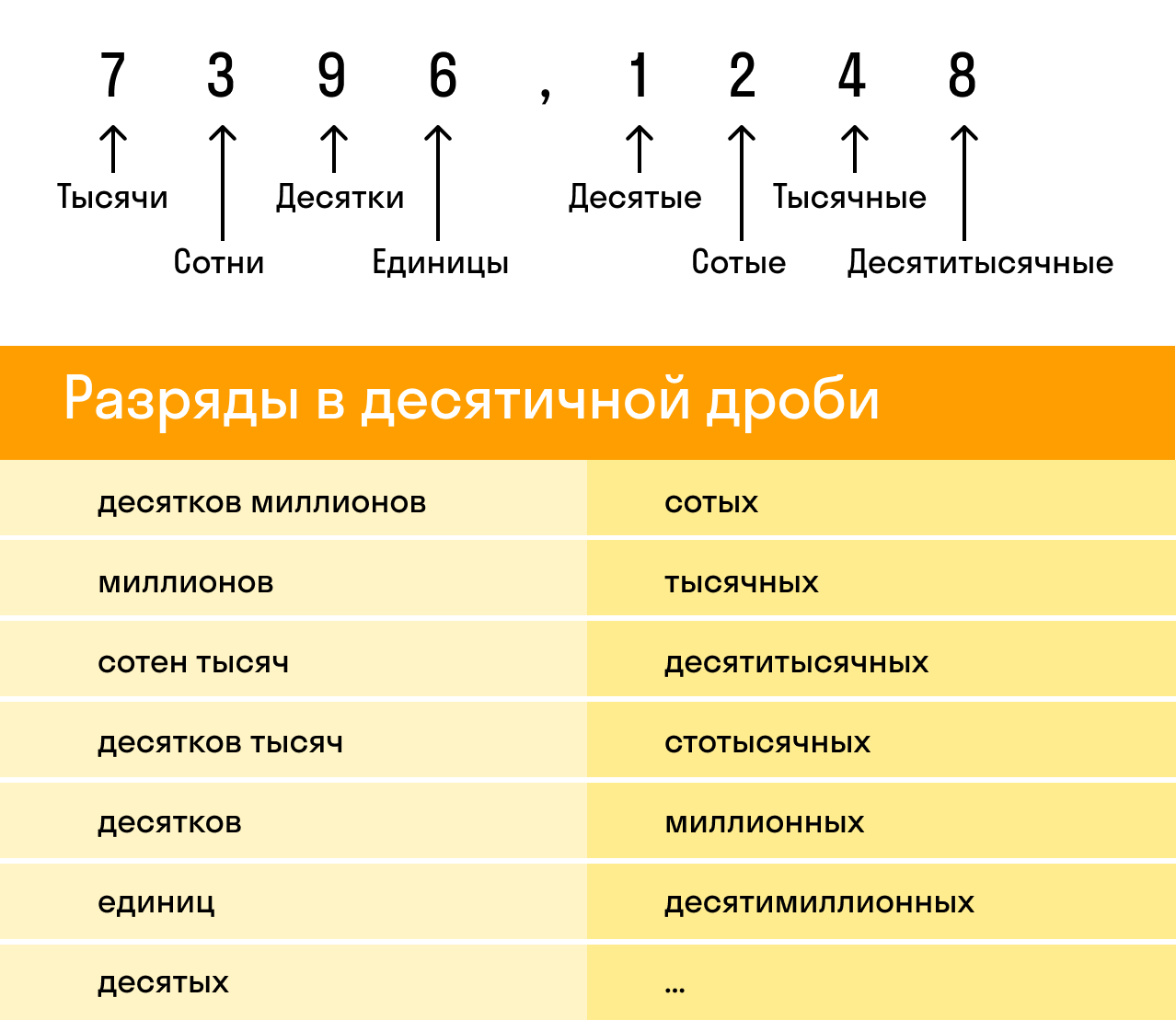
Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:
Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.
То число, к которому дробь ближе, называют округленным значением числа.
Цифра, которая записана в данном разряде:
Как округлить до десятых. Оставить одну цифру после запятой, остальные отбросить. Согласно правилу выше, если первая отбрасываемая цифра — 0, 1, 2, 3 или 4, то цифра после запятой остается той же. Если мы отбрасываем цифру 5, 6, 7, 8 или 9 — цифра после запятой увеличивается на единицу.
Как округлить до сотых. Оставить две цифры после запятой, остальные отбросить. И снова не забываем про правило: если следующая цифра 0, 1, 2, 4 — цифра в разряде сотых остается неизменной. Если же это 5, 6, 7, 8 или 9, то цифра в разряде сотых увеличится на 1.
Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.
Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.
Пример 1
256,43 ≈ 256,4 — округление до десятых;
4,578 ≈ 4,58 — округление до сотых;
17,935 ≈ 18 — округление до целых.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.
Пример 2
79,7 ≈ 80 — округление до десятков;
0,099 ≈ 0,10 — округление до сотых.
Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса.
Приближённые вычисления в математике
Содержание:
Приближённые вычисления
Приближённые вычисления — вычисления, в которых данные и результат (или только результат) являются числами, приближенно представляющими истинные значения соответствующих величин. Числовые данные, полученные измерением реальных объектов, редко бывают точными значениями соответствующей величины, а обычно имеют некоторую погрешность
Абсолютная и относительная погрешности
При решении практических задач часто приходится иметь дело с приближёнными значениями разных числовых величин. К ним относятся: результаты измерения разных величин с помощью приборов; значения полученные при считывании на графиках, диаграммах, номограммах; проектные данные; результаты округления чисел; результаты действий над приближёнными числами; табличные значения некоторых величин; результаты вычислений значений функции. Приближённые значения (приближение, приближённые числа) могут значительно отличаться от точных, либо быть близкими к ним.
Для оценки отклонения приближённых чисел от точных используют такие понятия как абсолютная и относительная погрешности.
Абсолютной погрешностью приближённой называется модуль разности между точным значением величины 
Пример.
Абсолютная погрешность приближённого числа 
Если точное число неизвестно, то найти абсолютную погрешность 

При записи приближённых чисел часто используют понятия верной и сомнительной цифры.
Цифра 
Например: в числе 

В конечной записи приближённого числа сохраняют только верные цифры. Так число 



Например: если 
Если в целом числе последние нули являются сомнительными, их исключают из записи числа.
Именно поэтому при работе с приближёнными числами широко используют стандартную форму записи числа.
Например: в числе 
Следовательно, в десятичной записи приближённого числа последняя цифра указывает на точность приближённости, то есть предел абсолютной погрешности не превышает единицу последнего разряда.
Например:
1. Запись 

2. Запись
3. Если
В десятичной записи числа значимыми цифрами называются все его верные цифры начиная с первой слева, отличной от нуля.
Например: в числе 1,13 — три значимых цифры, в числе 0,017 — две, в числе 0,303 — три, в числе 5,200 — четыре, в числе 25*10 3 — две значимых цифры.
При таком подходе к записи приближенного числа необходимо уметь округлять числа.
Правила округления чисел:
— Если первая цифра, которую отбрасываем является меньше пяти, то в основном разряде, который сохраняется цифра не меняется. Например: 879,673≈879,67.
— Если первая цифра, которую отбрасываем больше пяти, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 456,87≈456,9.
— Если первая цифра, которая отбрасывается пять и за ней есть ещё отличны от нуля, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 1246,5002≈1247.
— Если первая цифра, которая отбрасывается — пять и за ней нет больше никаких цифра, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 0,275≈0,28; 1,865≈1,86.
Абсолютная погрешность не полностью характеризует точность приближения. Например, 
Относительной погрешностью 


Поскольку абсолютная погрешность 
Число 
Предел относительной погрешности можно вычислить по формуле:
Конечно относительная погрешность выражается в процентах.
С помощью относительной погрешности легко установить точность приближённости.
Пример 1. Найти относительную погрешность числа
Решение: Имеем
Следовательно
Пример 2. Сравнить точность измерения толщины книги d (см) и высоты стола H (см), если известно, что 
Решение:
Как видим, точность измерения высоты стола значительно выше.
Выполнение действий над приближёнными числами
Результат арифметических действий над приближёнными числами является также приближённым числом.
Пример 3. Вычислить приближение значения выражения 
Решение: находим значение квадрата числа 5,62 и квадратного корня из числа 18,50.
Найдём границу относительной погрешности результата:
Граница абсолютной погрешности результата:
Ответ:
Пример 4. Вычислить приближение значения выражения 
Решение: находим значение квадратного корня из числа 6,24 и 
Граница относительной погрешности результата:
Граница абсолютной погрешности результата:
Ответ:
Выполнение действий без точного учёта погрешности
Точный учёт погрешности усложняет вычисление. Поэтому, если не надо учитывать погрешность промежуточных результатов, можно использовать более простые правила.
Сложение и вычитание приближённых вычислений рекомендуется выполнять так:
а) выделить слагаемое с наименьшим числом верных десятичных знаков;
б) округлить другие слагаемые так, чтобы каждое из них содержало на один десятичный знак больше чем выделенное;
в) выполнить действия, учитывая все сохранённые десятичные знаки;
г) результаты округлить и сохранить столько десятичных знаков, сколько их есть в приближённом числе с наименьшим числом десятичных знаков.
Умножение и деление приближённых вычислений рекомендуется выполнять так:
а) выделить среди данных чисел, число с наименьшим количеством верных значимых цифр;
б) округлить оставшиеся данные так, чтобы каждое из них содержало на одну значащую цифру больше, чем в выделенном;
в) выполнить действия — сохранить все значимые цифры;
г) сохранять в результате столько значащих цифр, сколько их имеет выделенное число с наименьшим количеством верных значимых цифр.
При возведении в степень приближённого числа в результате сохраняют столько значимых цифр, сколько верных значимых цифр имеет основа степени.
При извлечении корня из приближённого числа в результате сохраняют столько верных цифр, сколько имеет подкоренное число.
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Как писать цифры и числа в тексте? Правила русского языка
Правописание числительных в грамматике русского языка тема сложная.
Ну, во-первых, правила никто не отменял;
во-вторых, есть немало случаев, когда числительное, написанное цифрами, усложняет понимание текста, а также и наоборот;
в-третьих, сами правила совсем несложные, просто надо разложить их по полочкам, чем мы и займемся.
Вспомним, как могут записываться числа в тексте. Есть три формы написания:
Как писать цифры от 1 до 10 в тексте
Обычно пишутся прописью в тексте цифры от 1 до 10, особенно в косвенных падежах. В начале предложения — только в словесной форме.
Есть два исключения, когда применяется цифровая форма:
Порядковые числительные от 1 до 10 могут писаться, как прописью (в художественных и публицистических текстах это предпочтительней), так и в буквенно-цифровой форме. Буквы в этом случае называются наращением.
После цифры через дефис без пробелов ставится либо одна последняя буква окончания, либо две:
Это правило справедливо для всех порядковых числительных, как однозначных, так и многозначных.
Например: В мировую историю 2020-й год войдет в первую очередь как год пандемии коронавирусной инфекции. Для записи на собеседование подойдите к 47-му кабинету.
Как писать цифры прописью
С написанием цифр прописью в случае с однозначными числами разобрались. С двузначными и многозначными числами правила, приведенные выше, тоже работают.
В остальных случаях выбор формы написания числа вариативен и зависит от стиля текста (художественно-публицистический, научный, деловой и т.д.) и предпочтения автора.
Вот пример из художественного произведения:
Мне известен человек, который при росте примерно сто шестьдесят пять сантиметров носит обувь сорок пятого размера (В. Липатов)
Автор написал цифры прописью, чтобы у текста был именно художественный, а не деловой вид, но если предложение написать так: Мне известен человек, который при росте примерно 165 сантиметров носит обувь 45-го размера – это не будет ошибкой.
Тут надо ещё учитывать особенности восприятия чисел. Уже двузначные, а тем более числа с большим количеством разрядов, лучше воспринимаются в цифровой форме, хотя в художественном тексте, как правило, рекомендуют писать цифры прописью.
Чем больше число, тем сложнее облечь его при написании в словесную форму, и при этом не ошибиться в склонении. Да и надо ли это делать?
Сравните: В результате наводнения 2153 жителям пришлось экстренно покинуть свои дома.
Или: В результате наводнения двум тысячам ста пятидесяти трём жителям пришлось экстренно покинуть свои дома.
Как правильно писать цифры в документах
Но цифры пишутся и прописью:
Цифровая форма используется:
Буквенно-цифровая запись применяется:
Как писать цифры в скобках
В бухгалтерских, финансовых и юридических документах, разного рода заявлениях приходится сталкиваться с необходимостью писать цифры прописью в скобках для расшифровки денежных сумм, указанных перед этим в цифровых выражениях.
Для чего это делается легко догадаться с позиции простого здравого смысла. Дублируя цифровую запись буквенной, мы уменьшаем вероятность ошибки и возможного мошенничества. Подделать слова сложнее, чем цифры.
Записывать сумму прописью в скобках тоже надо правильно:
Например: Общая сумма контракта составляет 1 326 787 руб. 45 коп. (Один миллион триста двадцать шесть тысяч семьсот восемьдесят семь руб. 45 коп.)
Возможен и такой вариант написания, когда копейки пишутся один раз, скобки ставятся перед ними и в них расшифровывается только сумма в рублях (долларах, евро):
Общая сумма контракта составляет 1 326 787 руб. (Один миллион триста двадцать шесть тысяч семьсот восемьдесят семь руб.) 45 коп..
Мы разобрались, в каких случаях надо писать числительные прописью, а в каких – цифрами. Если с ходу не получается запомнить такое количество справочной информации, пользуйтесь этой статьей как памяткой и пишите цифры прописью правильно.
Кстати, у нас на сайте есть специальный инструмент “Перевод чисел в цифры прописью“. Если вам нужно быстро перевести цифры в готовый текст (или суммму), его удобно использовать.