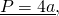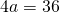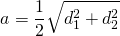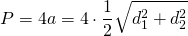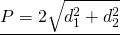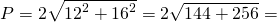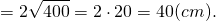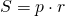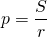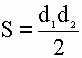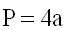Периметр ромба
Как найти периметр ромба, зная его сторону? Как найти периметр ромба по диагоналям? Как, если известен периметр ромба, найти его сторону?
Периметр ромба равен сумме длин всех его сторон.
Поскольку все стороны ромба равны, то формула периметра ромба
где a — длина стороны ромба.
1) Найти периметр ромба со стороной 7 см.
По формуле P=4a имеем: P=4∙7=28 (см).
2) Периметр ромба равен 36 см. Найти его сторону.
По формуле P=4a имеем:
Значит, сторона ромба равна 9 (см).
3) Найти периметр ромба, если его диагонали равны 12 см и 16 см.
Чтобы найти периметр ромба, нужно знать его сторону.
Отсюда приходим к формуле для нахождения периметра ромба по его диагоналям:
Значит, периметр ромба с диагоналями 12 см и 16 см равен
Одна из формул для нахождения площади ромба S связывает радиус r вписанной в ромб окружности и его полупериметр p:
Выразим p через S и r:
Так как P=2p, то приходим к формуле для нахождения периметра ромба через его площадь и радиус вписанной окружности
Формула нахождения периметра ромба
Периметр ромба
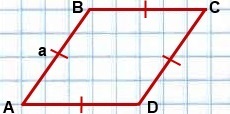
Ромб — это четырехугольник с равными сторонами.
Также его называют параллелограммом, у которого все ребра равны. При этом его противоположные углы тоже равны между собой. Если все углы равны 90 градусов, то это квадрат.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Способы нахождения
Рассмотрим все способы нахождения периметра этой фигуры.
По сторонам
Если нам известны величины одного из его ребер, мы без проблем можем найти P по формуле:
где a — это сторона ромба.
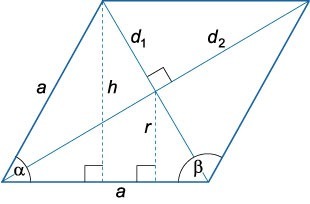
По двум диагоналям
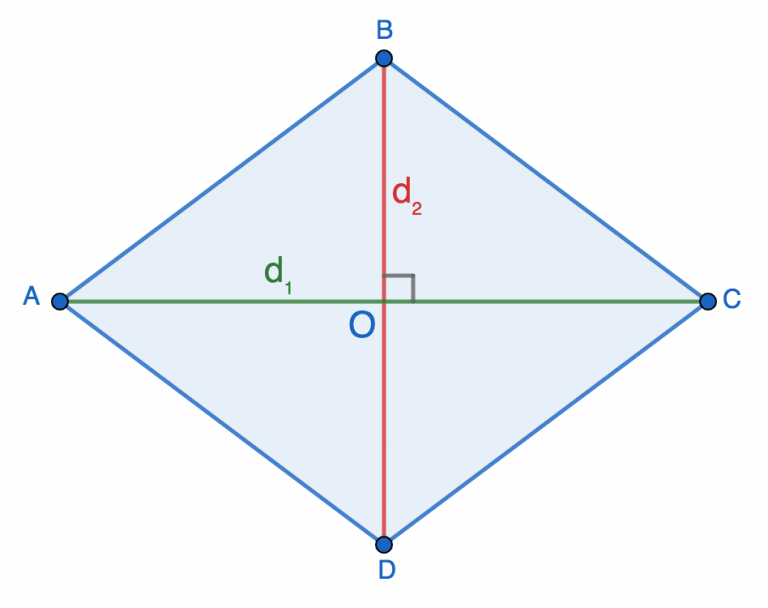
Если наш ромб — не квадрат, то две его диагонали будут не равны между собой. Также в любом ромбе они пересекаются под углом 90 градусов, а в точке пересечения делятся пополам. Если обе из них нам известны, то можем вычислить периметр фигуры следующим образом:
где \(d_1\) и \(d_2\) — это диагонали четырехугольника.
Подобные вычисления получились исходя из свойств диагоналей равностороннего четырехугольника. Вместе со сторонами фигуры они образуют прямоугольный треугольник. По теореме Пифагора:
По диагонали и углу
Чтобы вычислить сумму всех ребер ромба данным способом, для начала нужно определить величину одной стороны:
Далее расчет P будет выглядеть следующим образом:
По площади и радиусу вписанной окружности
По известной площади и радиусу вписанной окружности можно находить P, опираясь на формулу:
где r — это радиус вписанной окружности.
По площади и синусу одного из углов
В этом случае формула расчета суммы всех сторон выглядит так:
Формулы ромба
Формулы площади ромба:
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
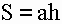
Формула периметра ромба:
1) Периметр ромба равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у ромба длины всех сторон равны).
Остались вопросы?
Здесь вы найдете ответы.
Высота ромба представляет собой перпендикуляр, который опущен из одного из его углов на сторону, противоположную данному углу.
Обозначим имеющийся ромб как ABCD. Из его угла В проведем высоту ВН, после чего получим треугольник АВН с прямым углом. Известно, что длина всех сторон ромба одинаковая, а длина АН равна половине длины АВ. Зная это и используя теорему, которая является обратной теореме о 30-градусном угле, можно провести доказательство того, что угол АВН равен 30 градусам.
Учитывая то, что сумма всех углов треугольника равна 180 градусом, можно найти неизвестную величину третьего угла треугольника:
Так, угол АВС равен:
Известна формула площади (S) ромба, которая представляет собой произведение длины его стороны (а) на высоту (h), проведенную к ней:
Есть возможность выразить высоту из приведенной выше формулы. Она будет равна отношению площади ромба к длине его стороны:
Площадь (S) треугольника с прямым углом рассчитывается путем деления пополам произведения длин его катетов. В данном случае она будет равна:
Площадь ромба определяется умножением длины его стороны на высоту, проведенную к ней. Если принять высоту за х, и учесть, что площадь ромба равна площади прямоугольного треугольника (6 см.кв.), то:
Отсюда можно найти значение х:
Ответ: высота ромба составляет 1,2 см.
Диагонали, проведенные в ромбе, делят эту фигуру на четыре треугольника, которые являются равными. Длины катетов этих треугольников составляют 3 см. и 4 см. Такой вывод можно сделать на основании того, что в точке пересечения диагоналей они делятся пополам. Гипотенуза (с) треугольников представляет собой сторону ромба. Ее длина равна:
Следовательно, сторона ромба также равна 5 см.
Площадь ромба высчитывается как произведение длин его диагоналей, деленное пополам:
S = d1*d2/2 = 6*8/2 = 24 см. кв.
Известна также другая формула, используемая для вычисления площади ромба, в которой длина его стороны (а) умножается на высоту(h):
Из данной формулы выражаем высоту:
Ответ: Высота ромба составляет 4,8 см.
Высоту ромба можно рассчитать, если его диагонали (d1 и d2)и сторона (а) – известные величинами. В этом случае для определения неизвестной высоты следует пользоваться приведенной ниже формулой:
Периметр (Р) ромба равен сумме длин всех его сторон (а) и вычисляется по следующей формуле:
В данном случае периметр ромба равен 48 см., это значит, что:
Находим значение а:
Площадь ромба (S) является произведением длины его стороны (а) и высоты (h), проведенной к этой стороне:
В задании сказано, что площадь ромба – 60 см.кв. Значит:
Находим неизвестную высоту:
Ответ: Высота ромба – 5 см.
Согласно формуле расчета периметра (Р) ромба, он равен сумме длин всех его сторон (а) (Р=а+а+а+а). Известно, что все стороны ромба имеет одинаковую длину. Из этого следует, что длина одной стороны будет равна ¼ части его периметра:
Площадь (S) ромба можно высчитать путем умножения длины его стороны (а) на высоту (h), проведенную к ней:
В конкретном случае:
Отсюда можем найти высоту (h), разделив площадь на длину стороны ромба:
Ответ: Высота ромба составляет 6 см.
Периметр (Р) ромба равен сумме длин всех его сторон (а), длины которых равны. Это значит:
Предположим, что длина одной из диагоналей ромба равна 10х, тогда длина второй его диагонали будет выглядеть как 24х. Отношение их длин можно записать в следующем виде:
Доказано, что диагонали ромба взаимно перпендикулярны и в точке пересечения они делятся пополам, при этом образуя четыре равных треугольника с прямым углом.
Теорема Пифагора гласит, что сумма длин его катетов, возведенных во вторую степень, равна длине гипотенузы, которая также возведена в квадрат:
Для данной задачи это равенство записывается так:
169х²=169; следовательно, х2 = 1. Значит х тоже будет равен 1.
Длина диаметра, обозначенного как 10х, равна 10 см. (10*1), а длина второго диаметра, который обозначен как 24х, равна 24 см. (24*1).
Площадь (S) ромба рассчитывается как:
Из этого можно составить следующее уравнение:
Выражаем h и получаем:
h= d₁*d₂/2*а=10·24:26=240/26=120/13 см.
Ромб имеет четыре высоты. Все они имеют равные длины. Вывод об этом можно сделать, рассмотрев все треугольные фигуры, элементами которых являются эти высоты. Есть возожность высчитать высоту ромба при помощи различных параметров, которые могут быть указаны в условии конкретной задачи.
Предположим, что нам известна площадь (S) ромба и длина его стороны (а). В этом случае высота ромба будет равна отношению его площади к длине высоты: h = S/a.
Если же по условию задачи известны длины диагоналей ромба d1 и d2, а также его сторона а, то высоту можно рассчитать так: h = (d1*d2 )/a.
В случае, когда известна длина стороны (а) ромба и угол А, находящийся между смежными сторонами, то для расчета высоты ромба используется следующая формула:
h = a*a*sin A /a = a*sin A.
Существуют также и другие варианты вычисления длины высоты ромба на основании того, какие величины будут известны по условию задания. Однако ключевыми параметрами, используя которые можно вычислить высоту ромба, являются диагонали, длина любой его стороны и угол, образованный между смежными сторонами.
Площадь ромба можно рассчитать одним из трех способов:
1. S = a² sin a, в которой α — образованный двумя сторонами угол, a — сторона.
2. S = ah, или Длина стороны ромба, умноженная на его высоту.
3. S = (d1*d2)/2, в которой d1 и d2 – длины диагоналей фигуры.
Зная, чему равен периметр ромба, можно вычислить длину его стороны:
Известно, что высота данной фигуры меньше ее стороны на 1,7 см. Теперь можем определить длину высоты:
Площадь ромба можно найти, умножив его сторону на высоту, которая на нее опущена:
Ответ: S = 50,4 см. кв.
Если длины диагоналей фигуры относятся как 4/3, то их половины будут относиться также:
(4d)²+(3d)²=10² = 16d²+9d² = 100
Теперь можно найти площадь:
S= 2*d¹/2*d²/2=2*8*6 = 96 см.кв.
Ответ: S ромба = 96 см.кв.
Площадь ромба можно описать как сумму площадей 2-х треугольных фигур, основанием которых является одна диагональ, а вторая диагональ ромба представляет собой сумму длин высот этих фигур. Диагонали ромба при пересечении образуют угол в 90 градусов. На основании этого можно найти площадь ромба следующим образом:
Известно, что, пересекаясь, диагонали ромба образуют угол в 90 градусов и в точке пересечения делятся пополам.
Для расчета площади ромба через диагонали нужно перемножить их длины, а затем разделить полученное число на два:
Для примера можно рассмотреть ромб, одна диагональ которого равна 5 см., а вторая – 4 см. Тогда его площадь будет равна:
S ромба возможно вычислить, перемножив длину одной из его сторон (а) и высоту (h). Формула записывается так:
Формулы ромба не по зубам? Тебе ответит эксперт через 10 минут!
Калькулятор периметра ромба
Ромб представляет собой параллелограмм, у которого все стороны равны, а углы непрямые. Частным случаем ромба считается квадрат, однако классическая фигура должна иметь два острых и два тупых угла. Ромбические элементы иногда встречаются в реальной жизни, поэтому поиск периметра косоугольника может быть не только школьным заданием, но и житейской задачей.
Геометрия ромба
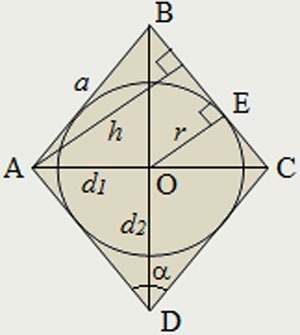
Ромб — это косоугольник с равными сторонами и равными высотами. Параллелограмм считается ромбом, если соблюдается хотя бы одно из перечисленных условий:
Несколько ромбов с одинаковой длиной стороны могут выглядеть совершенно по-разному. Все дело в различной величине внутренних углов, соответственно, для определения угла фигуры недостаточно знать только длину ее стороны. Для этого необходимо измерить диагонали ромбовидной фигуры, так как они разбивают четырехугольник на 4 прямоугольных треугольника. Кроме того, ромб — симметричная фигура, поэтому его диагонали одновременно являются осями симметрии и биссектрисами для углов, из которых они выходят.
Ромб в реальной жизни
В трехмерной повседневности ромб встречается не слишком часто: наибольшее применение он находит в металлообработке, машиностроении, архитектуре, геральдике и дизайне. К примеру, ромбовидную форму имеют резцы металлообрабатывающих станков, нестандартные ромбические окна или геометрические узоры на коврах или стенных покрытиях. Наиболее очевидным примером ромба в реальности является тротуарная плитка, которая чаще всего выполняется именно в ромбовидной форме. Кроме того, форму ромба имеют отличительные знаки выпускников военных училищ и гражданских учебных заведений. Несмотря на довольно скудное распространение в реальном мире, вам может понадобиться вычислить периметр ромба для решения каких-либо практических задач.
Периметр ромбической фигуры
Периметр вычисляется как сумма длин всех сторон плоской геометрической фигуры. Ромб — четырехугольник с равными между собой сторонами, а значит, его периметр определяется простой формулой:
где a — длина одной стороны.
Если вам необходимо найти периметр ромбовидной фигуры для решения школьных заданий или практических задач, воспользуйтесь нашим онлайн-калькулятором. Для определения периметра наиболее простым способом вам понадобится измерить только сторону ромба, однако алгоритм калькулятора требует ввода двух переменных, поэтому в форму «Высота» введите 1. Также вы можете определить периметр, введя следующие сочетания переменных:
Примеры из реальной жизни
Рассмотрим пару примеров.
Пример №1
Определите периметр ромба, если длина его стороны равна 6 см. Если дана сторона, то это самый простой способ для определения периметра. Если вы помните простую формулу, то просто умножьте длину на 4. Если же нет, то наш калькулятор к вашим услугам. Введите значение в форму калькулятора, укажите высоту равную 1 и получите простой ответ:
В школьных заданиях определение периметра может усложняться.
Пример №2
Найдите периметр ромбической фигуры, если длина одной его диагонали равна 8 см, а величина острого угла составляет 60 градусов. Решая эту задачу вручную, вам бы понадобилось определять длину стороны, используя тригонометрические расчеты. Однако при помощи нашего сервиса вы можете просто ввести эти данные в форму калькулятора и получить готовый результат в виде:
Вы можете вычислить периметр ромбической фигуры, оперируя разными параметрами. Кроме того, калькулятор автоматически подсчитает все остальные атрибуты ромба, как острый и тупой угол, длины обеих диагоналей и длину стороны.
Заключение
Несмотря на то, что ромбовидные фигуры редко встречаются в реальности, у вас может возникнуть потребность определения периметра ромба, как для решения абстрактных школьных заданий, так и бытовых или производственных вопросов. Используя наш инструментарий, вы быстро и без ошибок вычислите все необходимые атрибуты любой геометрической фигуры.
Ромб, свойства, признаки, формулы, площадь и периметр
Ромб, свойства, признаки, формулы, площадь и периметр.
Ромб – это параллелограмм, у которого все стороны равны.
Ромб (определение и понятие):
Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе – «бубен») – это параллелограмм, у которого все стороны равны.
Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма.
Ромбы отличаются друг от друга размером углов и длиной стороны.
Свойства ромба:
1. Противолежащие стороны ромба равны, т. к. все стороны ромба равны.
2. Противолежащие стороны ромба попарно параллельны.

3. Соседние углы ромба дополняют друг друга до 180°. Иными словами, сумма углов, прилежащих к любой из сторон ромба, равна 180°.
4. Диагонали ромба взаимно перпендикулярны.
5. Диагонали ромба точкой пересечения делятся пополам.
7. Диагонали ромба являются биссектрисами его углов и делят углы пополам.
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
8. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре.
9. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Признаки ромба:
Параллелограмм ABCD является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий:
– если две смежные стороны параллелограмма равны (отсюда следует, что все стороны равны), то он является ромбом.
AB = BC, то AB = BC = CD = AD;
– если диагонали параллелограмма пересекаются под прямым углом, то он является ромбом.
– если одна из диагоналей параллелограмма делит содержащие её углы пополам, то он является ромбом.
∠BAC = ∠CAD или ∠ABD = ∠DBC или ∠BCA = ∠ACD или ∠ADB = ∠BDC;
– если в параллелограмм можно вписать круг, то он является ромбом;
– если диагонали делят параллелограмм на четыре равных прямоугольных треугольника, то он является ромбом.
Примечание: © Фото https://www.pexels.com, https://pixabay.com

Мировая экономика
Справочники
Востребованные технологии
Поиск технологий
О чём данный сайт?
Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.
Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.
Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!
Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.
Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.
Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.
Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.