Как легко понять знаки Σ и П с помощью программирования
Для тех, кто подзабыл матешу
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Как пишется произведение в информатике
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Таблицы истинности и логические схемы
Теория к заданию 2 из ЕГЭ по информатике
Алгебра логики
Алгебра логики
Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях.
Основоположником алгебры логики является английский математик и логик Дж. Буль (1815–1864), положивший в основу своего логического учения аналогию между алгеброй и логикой. Любое высказывание он записывал с помощью символов разработанного им языка и получал «уравнения», истинность или ложность которых можно было доказать, исходя из определенных логических законов, таких как законы коммутативности, дистрибутивности, ассоциативности и др.
Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истина, ложь). Высказывания могут быть истинными, ложными или содержать истину и ложь в разных соотношениях.
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно.
Например, «3 умножить на 3 равно 9», «Архангельск севернее Вологды» — истинные высказывания, а «Пять меньше трех», «Марс — звезда» — ложные.
Очевидно, что не всякое предложение может быть логическим высказыванием, т. к. не всегда есть смысл говорить о его ложности или истинности. Например, высказывание «Информатика — интересный предмет» неопределенно и требует дополнительных сведений, а высказывание «Для ученика 10-А класса Иванова А. А. информатика — интересный предмет» в зависимости от интересов Иванова А. А. может принимать значение «истина» или «ложь».
Кроме двузначной алгебры высказываний, в которой принимаются только два значения — «истинно» и «ложно», существует многозначная алгебра высказываний. В такой алгебре, кроме значений «истинно» и «ложно», употребляются такие истинностные значения, как «вероятно», «возможно», «невозможно» и т. д.
В алгебре логики различаются простые (элементарные) высказывания, обозначаемые латинскими буквами (A, B, C, D, …), и сложные (составные), составленные из нескольких простых с помощью логических связок, например таких, как «не», «и», «или», «тогда и только тогда», «если … то». Истинность или ложность получаемых таким образом сложных высказываний определяется значением простых высказываний.
Обозначим как А высказывание «Алгебра логики успешно применяется в теории электрических схем», а через В — «Алгебра логики применяется при синтезе релейно-контактных схем».
Тогда составное высказывание «Алгебра логики успешно применяется в теории электрических цепей и при синтезе релейно-контактных схем» можно кратко записать как А и В; здесь «и» — логическая связка. Очевидно, что поскольку элементарные высказывания А и В истинны, то истинно и составное высказывание А и В.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Логических значений всего два: истина (TRUE) и ложь (FALSE). Это соответствует цифровому представлению — 1 и 0. Результаты каждой логической операции можно записать в виде таблицы. Такие таблицы называют таблицами истинности.
Основные операции алгебры логики
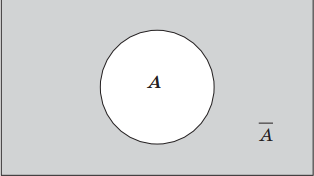
1. Логическое отрицание, инверсия (лат. inversion — переворачивание) — логическая операция, в результате которой из данного высказывания (например, А) получается новое высказывание (не А), которое называется отрицанием исходного высказывания, обозначается символически чертой сверху ($A↖<->$) или такими условными обозначениями, как ¬, ‘not’, и читается: «не А», «А ложно», «неверно, что А», «отрицание А». Например, «Марс — планета Солнечной системы» (высказывание А); «Марс — не планета Солнечной системы» ($A↖<->$); высказывание «10 — простое число» (высказывание В) ложно; высказывание «10 — не простое число» (высказывание B ) истинно.
Операция, используемая относительно одной величины, называется унарной. Таблица значений данной операции имеет вид
| A | ¬A |
| истина | ложь |
| ложь | истина |
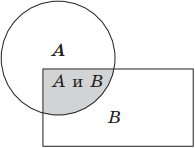
2. Конъюнкция (лат. conjunctio — соединение) — логическое умножение, операция, требующая как минимум двух логических величин (операндов) и соединяющая два или более высказываний при помощи связки «и» (например, «А и В»), которая символически обозначается с помощью знака ∧ (А ∧ В) и читается: «А и В». Для обозначения конъюнкции применяются также следующие знаки: А ∙ В; А & В, А and В, а иногда между высказываниями не ставится никакого знака: АВ. Пример логического умножения: «Этот треугольник равнобедренный и прямоугольный». Данное высказывание может быть истинным только в том случае, если выполняются оба условия, в противном случае высказывание ложно.
Таблица истинности операции имеет вид
| A | B | A ∧ B |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | ложь |
| истина | истина | истина |
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∧ В истинно только тогда, когда оба высказывания — А и В истинны.
Геометрически конъюнкцию можно представить следующим образом: если А, В — это некоторые множества точек, то А ∧ В есть пересечение множеств А и В.
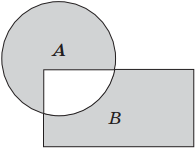
3. Дизъюнкция (лат. disjunction — разделение) — логическое сложение, операция, соединяющая два или более высказываний при помощи связки «или» (например, «А или В»), которая символически обозначается с помощью знака ∨ (А ∨ В) и читается: «А или В». Для обозначения дизъюнкции применяются также следующие знаки: А + В; А or В; А | B. Пример логического сложения: «Число x делится на 3 или на 5». Это высказывание будет истинным, если выполняются оба условия или хотя бы одно из условий.
Таблица истинности операции имеет вид
| A | B | A ∨ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | истина |
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∨ В ложно только тогда, когда оба высказывания — А и В ложны.
Геометрически логическое сложение можно представить следующим образом: если А, В — это некоторые множества точек, то А ∨ В — это объединение множеств А и В, т. е. фигура, объединяющая и квадрат, и круг.
4. Дизъюнкция строго-разделительная, сложение по модулю два — логическая операция, соединяющая два высказывания при помощи связки «или», употребленной в исключающем смысле, которая символически обозначается с помощью знаков ∨ ∨ или ⊕ (А ∨ ∨ В, А ⊕ В) и читается: «либо А, либо В». Пример сложения по модулю два — высказывание «Этот треугольник тупоугольный или остроугольный». Высказывание истинно, если выполняется какое-то одно из условий.
Таблица истинности операции имеет вид
| А | В | А ⊕ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | ложь |
| А | В | А ⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.
5. Импликация (лат. implisito — тесно связываю) — логическая операция, соединяющая два высказывания при помощи связки «если. то» в сложное высказывание, которое символически обозначается с помощью знака → (А → В) и читается: «если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяется также знак ⊃ (A ⊃ B). Пример импликации: «Если полученный четырехугольник квадрат, то около него можно описать окружность». Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием. Результат операции ложен только тогда, когда предпосылка есть истина, а следствие — ложь. Например, «Если 3 * 3 = 9 (А), то Солнце — планета (В)», результат импликации А → В — ложь.
Таблица истинности операции имеет вид
| А | В | А → В |
| истина | ложь | ложь |
| ложь | истина | истина |
| ложь | ложь | истина |
| истина | истина | истина |
| А | В | А → В |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина.
6. Эквивалентность, двойная импликация, равнозначность (лат. aequalis — равный и valentis — имеющий силу) — логическая операция, позволяющая из двух высказываний А и В получить новое высказывание А ≡ В, которое читается: «А эквивалентно B». Для обозначения эквивалентности применяются также следующие знаки: ⇔, ∼. Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Примером эквивалентности является высказывание: «Треугольник будет прямоугольным тогда и только тогда, когда один из углов равен 90 градусам».
Таблица истинности операции эквивалентности имеет вид
| А | В | А ∼ В |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | истина |
| истина | истина | истина |
| А | В | А ∼ В |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Операция эквивалентности противоположна сложению по модулю два и имеет результат «истина» тогда и только тогда, когда значения переменных совпадают.
Зная значения простых высказываний, можно на основании таблиц истинности определить значения сложных высказываний. При этом важно знать, что для представления любой функции алгебры логики достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
| Сложение по модулю два | А ⊕ В | $(A↖ <->∧B) ∧ (A ∧ B↖<->)$ |
| Импликация | А → В | $A↖ <->∨ B$ |
| Эквивалентность | А ∼ В | $(A↖ <->∧ B↖<->) ∨ (A ∧ B)$ |
Приоритет выполнения логических операций следующий: отрицание («не») имеет самый высокий приоритет, затем выполняется конъюнкция («и»), после конъюнкции — дизъюнкция («или»).
С помощью логических переменных и логических операций любое логическое высказывание можно формализовать, т. е. заменить логической формулой. При этом элементарные высказывания, образующие составное высказывание, могут быть абсолютно не связаны по смыслу, но это не мешает определять истинность или ложность составного высказывания. Например, высказывание «Если пять больше двух (А), то вторник всегда наступает после понедельника (В)» — импликация А → В, и результат операции в данном случае — «истина». В логических операциях смысл высказываний не учитывается, рассматривается только их истинность или ложность.
Рассмотрим, например, построение составного высказывания из высказываний А и В, которое было бы ложно тогда и только тогда, когда оба высказывания истинны. В таблице истинности для операции сложения по модулю два находим: 1 ⊕ 1 = 0. А высказывание может быть, например, таким: «Этот мяч полностью красный или полностью синий». Следовательно, если утверждение А «Этот мяч полностью красный» — истина, и утверждение В «Этот мяч полностью синий» — истина, то составное утверждение — ложь, т. к. одновременно и красным, и синим мяч быть не может.
Примеры решения задач
Пример 3. Для каких из приведенных слов ложно высказывание ¬(первая буква гласная ∧ третья буква гласная) ⇔ строка из 4 символов? 1) асса; 2) куку; 3) кукуруза; 4) ошибка; 5) силач.
Решение. Рассмотрим последовательно все предложенные слова:
1) для слова асса получим: ¬(1 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
2) для слова куку получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
3) для слова кукуруза получим: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 — высказывание ложно;
4) для слова ошибка получим: ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 — высказывание истинно;
5) для слова силач получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 — высказывание ложно.
Логические выражения и их преобразование
Под логическим выражением следует понимать такую запись, которая может принимать логическое значение «истина» или «ложь». При таком определении среди логических выражений необходимо различать:
Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения действий следующий:
В логическом выражении могут использоваться скобки, которые изменяют порядок выполнения операций.
Пример. Найти значение выражения:
Решение. Порядок подсчета значений:
1) b a + a b > a + b, после подстановки получим: 3 2 + 2 3 > 2 + 3, т. е. 17 > 2 + 3 = истина;
2) A ∧ B = истина ∧ ложь = ложь.
Следовательно, выражение в скобках равно (b a + a b > a + b ∨ A ∧ B) = истина ∨ ложь = истина;
3) 1≤ a = 1 ≤ 2 = истина;
Из логических элементов составляются электронные логические схемы, выполняющие более сложные логические операции. Набор логических элементов, состоящий из элементов НЕ, ИЛИ, И, с помощью которых можно построить логическую структуру любой сложности, называется функционально полным.
Построение таблиц истинности логических выражений
Для логической формулы всегда можно записать таблицу истинности, т. е. представить заданную логическую функцию в табличном виде. В этом случае таблица должна содержать все возможные комбинации аргументов функции (формулы) и соответствующие значения функции (результаты формулы на заданном наборе значений).
Если функция принимает значение 1 при всех наборах значений переменных, она является тождественно-истинной; если при всех наборах входных значений функция принимает значение 0, она является тождественно-ложной; если набор выходных значений содержит как 0, так и 1, функция называется выполнимой. Приведенный выше пример является примером тождественно-истинной функции.
Зная аналитическую форму логической функции, всегда можно перейти к табличной форме логических функций. С помощью заданной таблицы истинности можно решить обратную задачу, а именно: для заданной таблицы построить аналитическую формулу логической функции. Различают две формы построения аналитической зависимости логической функции по таблично заданной функции.
1. Дизъюнктивно нормальная форма (ДНФ) — сумма произведений, образованных из переменных и их отрицаний для ложных значений.
Алгоритм построения ДНФ следующий:
Пример. Построить функцию, определяющую, что первое число равно второму, используя метод ДНФ. Таблица истинности функции имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 1. Это первая и четвертая строки таблицы (строку заголовка при нумерации не учитываем).
2. Конъюнктивно нормальная форма (КНФ) — произведение сумм, образованных из переменных и их отрицаний для истинных значений.
Алгоритм построения КНФ следующий:
Примеры решения задач
Пример 1. Рассмотрим предыдущий пример, т. е. построим функцию, определяющую, что первое число равно второму, используя метод КНФ. Для заданной функции ее таблица истинности имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 0. Это вторая и третья строки (строку заголовка при нумерации не учитываем).
Таким образом, получена запись логической функции в КНФ.
Пример 2. Построить логическую функцию для заданной таблицы истинности:
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Решение. Используем алгоритм ДНФ для построения исходной функции:
| X1 | X2 | F(X1, X2) | ||
| 1 | 1 | 1 | • | X1 ∧ X2 |
| 1 | 0 | 0 | ||
| 0 | 1 | 1 | • | $ |
| 0 | 0 | 0 |
Пример 3. Для приведенной таблицы истинности построить логическую функцию, используя метод ДНФ.
Формула достаточно громоздка, и ее следует упростить:
Таблицы истинности для решения логических задач
Составление таблиц истинности — один из способов решения логических задач. При использовании такого способа решения, условия, которые содержит задача, фиксируются с помощью специально составленных таблиц.
Примеры решения задач
Пример 1. Составить таблицу истинности для охранного устройства, которое использует три датчика и срабатывает при замыкании только двух из них.
Решение. Очевидно, что результатом решения будет таблица, в которой искомая функция Y(X1, X2, X3) будет иметь значение «истина», если какие-либо две переменные имеют значение «истина».
| X1 | X2 | X3 | Y(X1, X2, X3) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Пример 2. Составить расписание уроков на день, учитывая, что урок информатики может быть только первым или вторым, урок математики — первым или третьим, а физики — вторым или третьим. Возможно ли составить расписание, удовлетворив всем требованиям? Сколько существует вариантов расписания?
Решение. Задача легко решается, если составить соответствующую таблицу:
| 1-й урок | 2-й урок | 3-й урок | |
| Информатика | 1 | 1 | 0 |
| Математика | 1 | 0 | 1 |
| Физика | 0 | 1 | 1 |
Из таблицы видно, что существуют два варианта искомого расписания:
Пример 3. В спортивный лагерь приехали трое друзей — Петр, Борис и Алексей. Каждый из них увлекается двумя видами спорта. Известно, что таких видов спорта шесть: футбол, хоккей, лыжи, плавание, теннис, бадминтон. Также известно, что:
Какими видами спорта увлекается каждый из мальчиков?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как видов спорта шесть, получается, что все мальчики увлекаются разными видами спорта.
Из условия 4 следует, что Борис не увлекается ни лыжами, ни теннисом, а из условий 3 и 5, что Петр не умеет играть в футбол, хоккей, теннис и бадминтон. Следовательно, любимые виды спорта Петра — лыжи и плавание. Занесем это в таблицу, а оставшиеся клетки столбцов «Лыжи» и «Плавание» заполним нулями.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | |||
| Алексей | 0 | 0 |
Из таблицы видно, что в теннис может играть только Алексей.
Из условий 1 и 2 следует, что Борис не футболист. Таким образом, в футбол играет Алексей. Продолжим заполнять таблицу. Внесем в пустые ячейки строки «Алексей» нули.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | 0 | ||
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Окончательно получаем, что Борис увлекается хоккеем и бадминтоном. Итоговая таблица будет выглядеть следующим образом:
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 1 | 0 | 0 | 1 | 0 |
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Ответ: Петр увлекается лыжами и плаванием, Борис играет в хоккей и бадминтон, а Алексей занимается футболом и теннисом.