Алгоритмы поиска на Python
Введение
Поиск информации, хранящейся в различных структурах данных, является важной частью практически каждого приложения.
Существует множество различных алгоритмов, которые можно использовать для поиска. Каждый из них имеет разные реализации и напрямую зависит от структуры данных, для которой он реализован.
Умение выбрать нужный алгоритм для конкретной задачи является ключевым навыком для разработчиков. Именно правильно подобранный алгоритм отличает быстрое, надежное и стабильное приложение от приложения, которое падает от простого запроса.
Операторы членства (Membership Operators)
Алгоритмы развиваются и оптимизируются в результате постоянной эволюции и необходимости находить наиболее эффективные решения для основных проблем в различных областях.
Одной из наиболее распространенных проблем в области компьютерных наук является поиск в коллекции и определение того, присутствует ли данный объект в коллекции или нет.
В Python самый простой способ поиска объекта — использовать операторы членства. Их название связано с тем, что они позволяют нам определить, является ли данный объект членом коллекции.
Эти операторы могут использоваться с любой итерируемой структурой данных в Python, включая строки, списки и кортежи.
Операторов членства достаточно, если нам нужно только определить, существует ли подстрока в данной строке, или пересекаются ли две строки, два списка или кортежа с точки зрения содержащихся в них объектов.
В большинстве случаев помимо определения, наличествует ли элемент в последовательности, нам нужна еще и позиция (индекс) элемента. Используя операторы членства, мы не можем получить ее.
Существует множество алгоритмов поиска, которые не зависят от встроенных операторов и могут использоваться для более быстрого и/или эффективного поиска значений. Кроме того, они могут дать больше информации (например, о позиции элемента в коллекции), а не просто определить, есть ли в коллекции этот элемент.
Линейный поиск
Линейный поиск — это один из самых простых и понятных алгоритмов поиска. Мы можем думать о нем как о расширенной версии нашей собственной реализации оператора in в Python.
Суть алгоритма заключается в том, чтобы перебрать массив и вернуть индекс первого вхождения элемента, когда он найден:
Итак, если мы используем функцию для вычисления:
То получим следующий результат:
Это индекс первого вхождения искомого элемента, учитывая, что нумерация элементов в Python начинается с нуля.
Линейный поиск не часто используется на практике, потому что такая же эффективность может быть достигнута с помощью встроенных методов или существующих операторов. К тому же, он не такой быстрый и эффективный, как другие алгоритмы поиска.
Линейный поиск хорошо подходит для тех случаев, когда нам нужно найти первое вхождение элемента в несортированной коллекции. Это связано с тем, что он не требует сортировки коллекции перед поиском (в отличие от большинства других алгоритмов поиска).
Бинарный поиск
Бинарный поиск работает по принципу «разделяй и властвуй». Он быстрее, чем линейный поиск, но требует, чтобы массив был отсортирован перед выполнением алгоритма.
Алгоритм бинарного поиска можно написать как рекурсивно, так и итеративно. В Python рекурсия обычно медленнее, потому что она требует выделения новых кадров стека.
Поскольку хороший алгоритм поиска должен быть максимально быстрым и точным, давайте рассмотрим итеративную реализацию бинарного поиска:
Если мы используем функцию для вычисления:
То получим следующий результат, являющийся индексом искомого значения:
На каждой итерации алгоритм выполняет одно из следующих действий:
Мы можем выбрать только одно действие на каждой итерации. Также на каждой итерации наш массив делится на две части. Из-за этого временная сложность двоичного поиска равна O(log n).
Одним из недостатков бинарного поиска является то, что если в массиве имеется несколько вхождений элемента, он возвращает индекс не первого элемента, а ближайшего к середине:
После выполнения этого фрагмента кода будет возвращен индекс среднего элемента:
Для сравнения: выполнение линейного поиска по тому же массиву вернет индекс первого элемента:
Однако мы не можем категорически утверждать, что двоичный поиск не работает, если массив содержит дубликаты. Он может работать так же, как линейный поиск, и в некоторых случаях возвращать первое вхождение элемента. Например:
Jump Search
Jump Search похож на бинарный поиск тем, что он также работает с отсортированным массивом и использует аналогичный подход «разделяй и властвуй» для поиска по нему.
Его можно классифицировать как усовершенствованный алгоритм линейного поиска, поскольку он зависит от линейного поиска для выполнения фактического сравнения при поиске значения.
Поскольку это сложный алгоритм, давайте рассмотрим пошаговое вычисление для следующего примера:
Временная сложность jump search равна O(√n), где √n — размер прыжка, а n — длина списка. Таким образом, с точки зрения эффективности jump search находится между алгоритмами линейного и бинарного поиска.
Единственное наиболее важное преимущество jump search по сравнению с бинарным поиском заключается в том, что он не опирается на оператор деления ( / ).
В большинстве процессоров использование оператора деления является дорогостоящим по сравнению с другими основными арифметическими операциями (сложение, вычитание и умножение), поскольку реализация алгоритма деления является итеративной.
Стоимость сама по себе очень мала, но когда количество искомых элементов очень велико, а количество необходимых операций деления растет, стоимость может постепенно увеличиваться. Поэтому jump search лучше бинарного поиска, когда в системе имеется большое количество элементов: там даже небольшое увеличение скорости имеет значение.
Чтобы ускорить jump search, мы могли бы использовать бинарный поиск или какой-нибудь другой алгоритм для поиска в блоке вместо использования гораздо более медленного линейного поиска.
Поиск Фибоначчи
Поиск Фибоначчи — это еще один алгоритм «разделяй и властвуй», который имеет сходство как с бинарным поиском, так и с jump search. Он получил свое название потому, что использует числа Фибоначчи для вычисления размера блока или диапазона поиска на каждом шаге.
Числа Фибоначчи — это последовательность чисел 0, 1, 1, 2, 3, 5, 8, 13, 21 …, где каждый элемент является суммой двух предыдущих чисел.
fibM = fibM_minus_1 + fibM_minus_2
Мы инициализируем значения 0, 1, 1 или первые три числа в последовательности Фибоначчи. Это поможет нам избежать IndexError в случае, когда наш массив lys содержит очень маленькое количество элементов.
Давайте посмотрим на реализацию этого алгоритма на Python:
Используем функцию FibonacciSearch для вычисления:
Давайте посмотрим на пошаговый процесс поиска:
Получаем ожидаемый результат:
Временная сложность поиска Фибоначчи равна O(log n). Она такая же, как и у бинарного поиска. Это означает, что алгоритм в большинстве случаев работает быстрее, чем линейный поиск и jump search.
Поиск Фибоначчи можно использовать, когда у нас очень большое количество искомых элементов и мы хотим уменьшить неэффективность, связанную с использованием алгоритма, основанного на операторе деления.
Дополнительным преимуществом использования поиска Фибоначчи является то, что он может вместить входные массивы, которые слишком велики для хранения в кэше процессора или ОЗУ, потому что он ищет элементы с увеличивающимся шагом, а не с фиксированным.
Экспоненциальный поиск
Экспоненциальный поиск — это еще один алгоритм поиска, который может быть достаточно легко реализован на Python, по сравнению с jump search и поиском Фибоначчи, которые немного сложны. Он также известен под названиями galloping search, doubling search и Struzik search.
Экспоненциальный поиск зависит от бинарного поиска для выполнения окончательного сравнения значений. Алгоритм работает следующим образом:
Реализация алгоритма экспоненциального поиска на Python:
Используем функцию, чтобы найти значение:
Рассмотрим работу алгоритма пошагово.
Функция вернет следующий результат:
Этот результат является индексом искомого элемента как в исходном списке, так и в срезе, который мы передаем алгоритму бинарного поиска.
Экспоненциальный поиск выполняется за время O(log i), где i — индекс искомого элемента. В худшем случае временная сложность равна O(log n), когда искомый элемент — это последний элемент в массиве (n — это длина массива).
Экспоненциальный поиск работает лучше, чем бинарный, когда искомый элемент находится ближе к началу массива. На практике мы используем экспоненциальный поиск, поскольку это один из наиболее эффективных алгоритмов поиска в неограниченных или бесконечных массивах.
Интерполяционный поиск
Интерполяционный поиск — это еще один алгоритм «разделяй и властвуй», аналогичный бинарному поиску. В отличие от бинарного поиска, он не всегда начинает поиск с середины. Интерполяционный поиск вычисляет вероятную позицию искомого элемента по формуле:
В этой формуле используются следующие переменные:
Алгоритм осуществляет поиск путем вычисления значения индекса:
Давайте посмотрим на реализацию интерполяционного поиска на Python:
Если мы используем функцию для вычисления:
Наши начальные значения будут следующими:
index = 0 + [(6-1)*(7-0)/(8-1)] = 5
Поскольку lys[5] равно 6, что является искомым значением, мы прекращаем выполнение и возвращаем результат:
Если у нас большое количество элементов и наш индекс не может быть вычислен за одну итерацию, то мы продолжаем пересчитывать значение индекса после корректировки значений high и low.
Временная сложность интерполяционного поиска равна O(log log n), когда значения распределены равномерно. Если значения распределены неравномерно, временная сложность для наихудшего случая равна O(n) — так же, как и для линейного поиска.
Интерполяционный поиск лучше всего работает на равномерно распределенных, отсортированных массивах. В то время как бинарный поиск начинает поиск с середины и всегда делит массив на две части, интерполяционный поиск вычисляет вероятную позицию элемента и проверяет индекс, что повышает вероятность нахождения элемента за меньшее количество итераций.
Зачем использовать Python для поиска?
Python очень удобочитаемый и эффективный по сравнению с такими языками программирования, как Java, Fortran, C, C++ и т. д. Одним из ключевых преимуществ использования Python для реализации алгоритмов поиска является то, что вам не нужно беспокоиться о приведении или явной типизации.
В Python большинство алгоритмов поиска, которые мы обсуждали, будут работать так же хорошо, если мы ищем строку. Имейте в виду, что понадобится внести изменения в код для алгоритмов, которые используют искомый элемент для числовых вычислений, например алгоритм интерполяционного поиска.
Python также подходит, если вы хотите сравнить производительность различных алгоритмов поиска для вашего dataset’а. Создание прототипа на Python проще и быстрее, потому что вы можете сделать больше с меньшим количеством строк кода.
Чтобы сравнить производительность наших реализованных алгоритмов, в Python мы можем использовать библиотеку time:
Заключение
Существует множество возможных способов поиска элемента в коллекции. В этой статье мы обсудили несколько алгоритмов поиска и их реализации на Python.
Выбор используемого алгоритма зависит от данных, с которыми вы будете работать. Это ваш входной массив, который мы называли lys во всех наших реализациях.
Если вы не уверены, какой алгоритм использовать для отсортированного массива, просто протестируйте каждый из них при помощи библиотеки time и выберите тот, который лучше всего работает с вашим dataset’ом.
Базовые алгоритмы с помощью Python
Немного про алгоритмизацию и псевдокод
Алгоритмизация — очень важная штука в жизни программиста. Все владеют этим навыком на разном уровне, однако владеть базовыми вещами должен каждый.
Во многих книгах для алгоритмов используется особый язык — псевдокод.

Как мы видим, тут используются отступы, символ ∈ для перебора элементов множества и многое другое, что в обычных языках не увидишь. Однако если внимательно посмотреть, то многое станет понятным. Использовать псевдокод сегодня мы не будем, информация предоставлена для дополнительного понимания происходящего.
Что здесь будет происходить?
Существует куча алгоритмов, подходящих для определенной задачи. Сегодня мы посмотрим на три базовых алгоритма, о которых будет чуть позже.
Данная статья будет по такой схеме:
Надеюсь всё понятно, теперь поговорим о языке, который мы будем использовать.
Python
Для демонстрации работы таких алгоритмов в реальном языке программирования нам необходим очень понятный и интуитивно понятный синтаксис. Как вы уже поняли из названия, в качестве такого языка я выбрал Python. Объясню несколько вещей, которые могут быть непонятны тем, кто не работал с этим языком:
a, b = b, a — распаковка кортежа(в данном случае обмен значениями двух переменных).
for a in list: — перебор всех элементов массива(эквивалентно foreach в C#)
while a
Т.к. b в определенный момент может стать больше a, при такой ситуации «свапаем» их значения.
Тестирование
Выглядеть это всё дело будет примерно так:
Теперь оформим тестирование. Для этого воспользуемся форматированием строки.
Конструкция a, b = pair — распаковывает кортеж, присваивая переменной a значение pair[0], а переменной b — pair[1]. Далее подставляем все необходимые значения в строку и смотрим результат:
Все тесты наш алгоритм прошел, что не может не радовать. Теперь подумаем над улучшением нашего алгоритма.
Улучшение
Сейчас нам предстоит подумать над улучшением алгоритма. Мы можем убрать распаковку кортежа и просто через конструкцию if/else изменять числа. Выглядеть это будет так:
Заново протестируем наш алгоритм:
Результат всё тот же. Мы немного улучшили алгоритм и улучшили его читабельность(всё-таки распаковка кортежа может быть кому-то непонятна), при этом не повлияв на результат его работы.
Решето Эратосфена
Реализация
Задача: вывести все простые числа до натурального числа a(a > 2).
Ввод: a ∈ N
Для такой задачи возможно использование простого перебора, однако это будет неэффективно. Здесь мы будем использовать решето Эратосфена, подробное описание есть в Википедии(там даже есть интересная наглядная анимация работы этого алгоритма).
Для тех, кому лень читать, объясню кратко. Суть такова: мы создаем массив всех натуральных чисел от 2 до a по возрастанию. Затем мы берём каждый индекс i и приравниваем к нулю каждый элемент с индексом k*i(k = 1, 2, 3, …).
Здесь мы создаем маску, заполненную единицами(мы можем заменить 1 и 0 на True, False соответственно).
Далее работаем с индексами с помощью вложенного цикла. Здесь мы меняем значения в маске, а позже по маске осуществляем выбор элементов из массива. Для простоты пользуемся методом типа list — list.append().
Тестирование
По традиции, вручную создадим несколько тестов. Алгоритм довольно прост, потому нам понадобятся 3 наборa.
Также само тестируем алгоритм:
Улучшение
Если рассматривать пути улучшения, то можно убрать выбор по маске и воспользоваться возможностями языка в помощи очистки массива от полученных нулей. Получим нечто такое:
С помощью конструкции list(set()) мы очищаем массив от повторений. Затем удаляем лишний ноль и сортируем массив, из-за того, что set() не сохраняет порядок.
Однако такой метод мне не очень нравится, поскольку мы использовали слишком много особенных возможностей языка.
Бинарный поиск
Реализация
Задача: дан отсортированный массив натуральных чисел. Также дано число K. Установить номер позиции, куда необходимо вставить K, чтобы массив не перестал был отсортированным. Если в массиве встречаются числа, равные K, вставлять K следует перед ними.
Ввод: K ∈ N, arr : array;
Для этой задачи подойдёт и способ перебора, однако он имеет линейную сложность (O(N)), а бинарный поиск(тот самый алгоритм, который мы сейчас будем реализовывать) имеет логарифмическую сложность — O(log(N)).
Немного про О большое. Оценка сложности алгоритма служит для понимания, как будут увеличиваться затраты на вычисление в зависимости от изменения вводных данных. Например, если нам на ввод подается число N и для вычисления нам потребуется два цикла, один из которых вложенный, длиною N, то сложность алгоритма оценивается как O(N^2). Обычно константы в О-большом откидываются, ведь никак не влияют на результат(это только отчасти правда, иногда именно константы решают всё).
Именно поэтому существует запись log(N). Разложим log 2 (N) = log A (N) / log A (2), где A — любое число больше нуля и не равны единице. Т.к. log A (2) это константа, то её мы откидываем. Получаем log A (N). А так как A любое число, то мы просто пишем log(N).
Суть бинарного поиска — разделение массива на две части и путём сравнения откидывание одной из них.
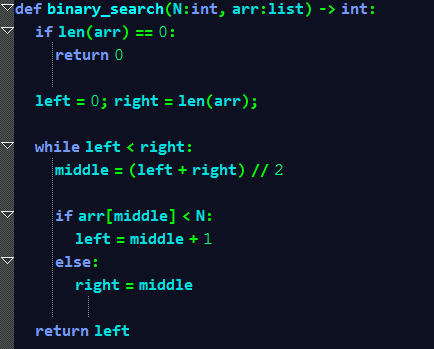
Для нашей задачи алгоритм будет выглядеть примерно так:
Отбираем особый случай, когда массив пуст, а дальше ничего сложного.
Тестирование
Теперь мы случайно будем генерировать тестовые данные. Для этого воспользуемся генераторами(не будем вникать в тонкости их работы, просто расскажу, что делает фрагмент кода ниже).
Наш генератор принимает два параметра: N — кол-во возвращаемых массивов и l — их длину. Далее создаем массив с помощью спискового включения, и увеличиваем коэффициенты для следующего.
Теперь, по образцу, запускаем тестирование.
Конечно же, у вас будут другие массивы, т.к. их мы генерируем с помощью random(не забудьте импортировать этот модуль в начале программы).
Насчет улучшения, то тут предоставлена стандартная реализация алгоритма, читабельная и понятная, потому пункт «Улучшение» мы пропустим.
Заключение
Сегодня мы реализовали три базовых алгоритма на языке Python. Вышло довольно неплохо, надеюсь полученные сегодня знания пригодятся вам в будущем. В этой статье переплетаются очень много тем, по которым можно написать отдельные материалы(например О-большое), так что можете попробовать найти интересную информацию об этом в интернете.
Весь код из статьи, разделенный по блокам, можете найти тут.
Также рекомендую прочитать статью Паттерн Декоратор (Decorator)
Основные алгоритмы и их реализация на Python
2.1 Линейные алгоритмы. Операции с числами и строками
Линейный алгоритм — алгоритм, в котором вычисления выполняются строго последовательно. Типичная блок-схема линейного алгоритма показана на рис. 2.1.
Далее рассмотрим типичные задачи с линейной структурой алгоритма.
Блок-схема такого алгоритма показана на рис. 2.2.
Текст программы на «псевдоязыке»:
Метод решения с использованием особенностей Python: использовать два кортежа. В первом будут определены переменные a и b и их значения, а второй сформируем из этих же переменных, но в обратном порядке.
Текст программы на Python:
# Перестановка местами двух чисел с использованием кортежа
(a, b)=input(‘Введите исходные значения (a, b) через запятую: ‘)
print ‘Новое значение а: ‘, a, ‘\n’, ‘Новое значение b: ‘, b
Как описано в разделе 1.4.2, комбинация ‘\n’ означает директиву на перевод строки для команды print.
Задача 2. Известны оклад (зарплата) и ставка процента подоходного налога. Определить размер подоходного налога и сумму, получаемую на руки.
Блок-схема алгоритма показана на рис. 2.3.
Текст программы на «псевдоязыке»:
Программа на Python:
print «Сумма на руки: «, summa
print «Налог: «, nalog
Если все числа в этом примере использовать как целые, то результат может получиться неверным. Поэтому при вычислении налога используется преобразование числителя из целого числа в вещественное (функция float() ).
Задача 3. Используя данные таблицы определить общую стоимость обеда в столовой. Определить, во сколько раз возрастёт стоимость обеда, если цена котлеты увеличится вдвое. 1 Источник: В.А.Молодцов, Н.Б.Рыжикова. Информатика: тесты, задания, лучшие методики. Ростов-на-Дону: Феникс, 2009.
Простой метапоисковый алгоритм на Python
Лирическое отступление
В рамках научно-исследовательской работы в вузе я столкнулся с такой задачей, как классификация текстовой информации. По сути, мне нужно было создать алгоритм, который, обрабатывая определенный текстовый документ на входе, вернул бы мне на выходе массив, каждый элемент которого являлся бы мерой принадлежности этого текста (вероятностью или степенью уверенности) к одной из заданных тематик.
В данной статье речь пойдет не о решении задачи классификации конкретно, а о попытке автоматизировать наиболее скучный этап разработки рубрикатора — создание обучающей выборки.
Когда лень работать руками
Первая и самая очевидная для меня мысль – написать простой метапоисковый алгоритм на Python. Другими словами, вся автоматизация сводится к использованию выдачи другой поисковой машины (Google Search) за неимением своих баз данных. Сразу оговорюсь, есть уже готовые библиотеки, решающие подобную задачу, например pygoogle.
Ближе к делу
Для HTTP-запросов я использовал requests, а для извлечения ссылок из поисковой выдачи — библиотеку для парсинга BeautifulSoup. Вот что получилось:
Я дергал лишь ссылки на сайты, которые на странице результатов поиска Chrome находятся внутри тэгов
Чтож, отлично, теперь попробуем забрать ссылки, обойдя несколько страниц браузера:
Адрес следующей страницы Chrome хранит в тэге
Ну и напоследок попробуем достать информацию с какой-нибудь страницы и сделать из нее словарь для будущего рубрикатора. Забирать необходимую информацию будем с той же Википедии:
Для запроса «god» получается неплохой такой словарь на 3.500 терминов, который, по правде говоря, придется дорабатывать напильником, удаляя знаки препинания, ссылки, стоп-слова и прочий «мусор».
Вывод
Подводя итог проделанной работы, надо заметить, что словарь конечно получился «сырой» и «натаскивание» парсера на конкретный ресурс требует времени на изучение его структуры. Это наталкивает на простую мысль — генерацию обучающей выборки стоит осуществлять самому, или пользоваться готовыми базами данных.
С другой стороны, при должной внимательности к написанию парсера (очистить html разметку от лишних тегов не составляет большого труда) и большом количестве классов, некоторая степень автоматизации может добавить рубрикатору необходимую гибкость.