Четырёхугольники
Четырёхугольник — это выпуклый многоугольник с четырьмя углами и четырьмя сторонами. Четырёхугольник образуется замкнутой ломаной линией, состоящей из четырёх звеньев, и той частью плоскости, которая находится внутри ломаной.
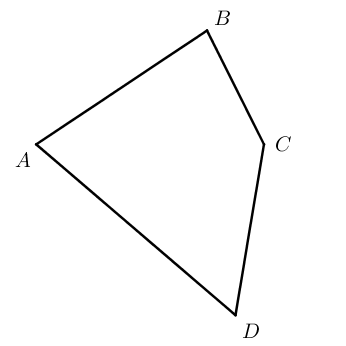
Обозначение четырёхугольника составляют из букв, стоящих при его вершинах, называя их по порядку. Например, говорят или пишут: четырёхугольник ABCD :
В четырёхугольнике ABCD точки A, B, C и D — это вершины четырёхугольника, отрезки AB, BC, CD и DA — стороны.
Вершины, принадлежащие одной стороне, называются соседними, вершины, не являющиеся соседними, называются противолежащими:
В четырёхугольнике ABCD вершины A и B, B и C, C и D, D и A — соседние, а вершины A и C, B и D — противолежащие. Углы, лежащие при соседних вершинах, также называются соседними, а при противолежащих вершинах — противолежащими.
Стороны четырёхугольника также можно попарно разделить на соседние и противолежащие: стороны, имеющие общую вершину, называются соседними (или смежными), стороны, не имеющие общих вершин — противолежащими:
Если противолежащие вершины соединить отрезком, то такой отрезок будет называться диагональю четырёхугольника. Учитывая, что в четырёхугольнике есть всего две пары противолежащих вершин, то и диагоналей может быть всего две:
Виды четырёхугольников
Рассмотрим основные виды выпуклых четырёхугольников:
Свойства углов выпуклых четырёхугольников
У всех выпуклых четырёхугольников углы обладают следующими двумя свойствами:
Четырехугольник
Определение четырехугольника
Определение 1. Четырехугольник − это замкнутая ломаная линия, состоящая из четырех звеньев.
Определение 2. Четырехугольник − геометрическая фигура (многоугольник), состоящая из четырех точек, никакие три из которых не лежат на одной прямой и последовательно соединенные четырьмя отрезками, называемыми сторонами четырехугольника.
Объединение четырехугольника и ограниченной им части плоскости также называют четырехугольником.
Любой четырехугольник разделяет плоскость на две части, одна из которых называется внутренней областью четырехугольника, а другая внешней областью четырехугольника.
Виды четырехугольников
Четырехугольники бывают следующих видов:
     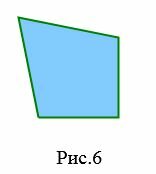   |
Обозначение четырехугольника
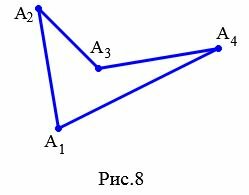
Обозначают четырехугольник буквами, стоящих при его вершинах. Называют четырехугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, четырехугольник на рисунке 8 называют \( \small A_1A_2A_3A_4 \) или \( \small A_4A_3A_2A_1 \) (Рис.8).
 |
Соседние вершины четырехугольника
Вершины четырехугольника называются соседними, если они являются концами одной из его сторон.
На рисунке 8 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)
Смежные стороны четырехугольника
Стороны четырехугольника называются смежными, если они имеют общую вершину.
На рисунке 8 стороны \( \small A_2A_3 \) и \( \small A_3A_4 \) являются смежными, так как они имеют общую вершину \( \small A_3. \)
Простой четырехугольник. Самопересекающийся четырехугольник
Четырехугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
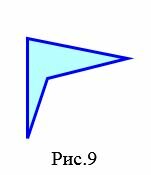  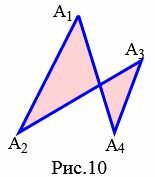 |
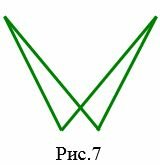
На рисунках 9 и 9.1 изображены простые четырехугольники так как стороны четырехугольников не имеют самопересечений. А на рисунке 10 четырехугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой четырехугольник называется самопересекающийся.
Выпуклый четырехугольник
Четырехугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
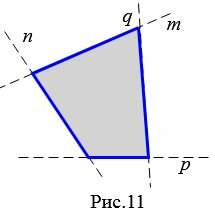 |
На рисунке 11 четырехугольник лежит по одну сторону от прямых \( \small m, \ n, \ p, \ q, \) проходящих через стороны четырехугольника. Поэтому такой четырехугольник выпуклый.
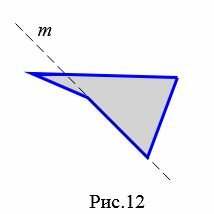 |
На рисунке 12 прямая \( \small m\) делит четырехугольник на две части, т.е. четырехугольник не лежит по одну сторону от прямой \( \small m\). Следовательно, этот четырехугольник не является выпуклым.
Правильный четырехугольник
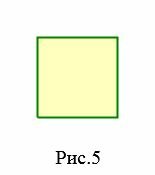
Простой четырехугольник называется правильным, если все его стороны равны и все углы равны. Квадрат является правильным четырехугольником, так как все его стороны равны и все его углы равны 90°. Среди четырехугольников других правильных четырехугольников не существует.
На рисунке 5 изображен правильный четырехугольник (квадрат), так как у данного четырехугольника все стороны равны и все углы равны. Четырехугольник (ромб) на на рисунке 4 не является правильным, так как все стороны четырехугольника равны, но все его углы не равны друг другу. Прямоугольник также не является правильным четырехугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Периметр четырехугольника
Сумма всех сторон четырехугольника называется периметром четырехугольника. Для четырехугольника \( \small A_1A_2A_3A_4 \) периметр вычисляется из формулы:
Угол четырехугольника
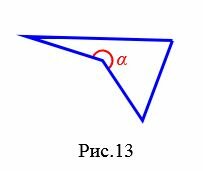
Углом (внутренним углом) четырехугольника при данной вершине называется угол между двумя сторонами четырехугольника, сходящимися к этой вершине. Если четырехугольник выпуклый, то все углы четырехугольника меньше 180°. Если же четырехугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small \alpha \) на рисунке 13).
 |
Внешний угол четырехугольника
Внешним углом четырехугольника при данной вершине называется угол смежный внутреннему углу четырехугольника при данной вершине.
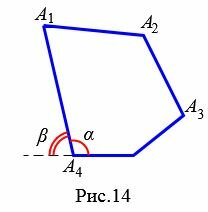 |
На рисунке 14 угол α является внутренним углом четырехугольника при вершине \( \small A_4, \) а углы β и γ являются внешними углами четырехугольника при этой же вершине. Очевидно, что при каждой вершине есть два внешних угла.
Диагональ четырехугольника
Диагоналями называют отрезки, соединяющие две несоседние вершины четырехугольника.
Очевидно, что у четырехугольника две диагонали.
Сумма углов четырехугольника
Для любого простого четырехугольника по крайней мере один диагональ делит его на два треугольника. Сумма углов треугольника равна 180°. Поэтому сумма углов простого четырехугольника равна 360°.
Сумма внешних углов четырехугольника
| \( \small 180°-\angle A_1 \) \( \small +180°-\angle A_2 \) \( \small +180°-\angle A_3 \) \( \small +180°-\angle A_4 \)\( \small =720°-(\angle A_1+\angle A_2+\angle A_3+\angle A_4 )\) \( \small =720°-360°=360°. \) |
Задача 1. Доказать, что длина любой стороны четырехугольника меньше суммы длин трех его сторон.
Обозначение геометрических фигур буквами
В математике есть правило: обозначать геометрические фигуры заглавными буквами латинского алфавита. Сегодня мы научимся этому.
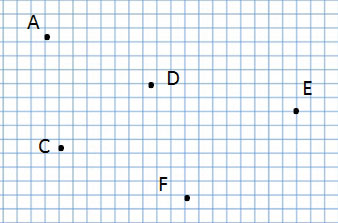
Точка
точка А, точка С, точка D, точка Е и точка F.
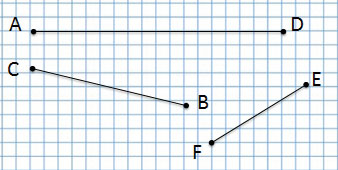
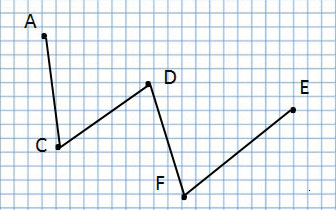
Отрезок
отрезок AD, отрезок СВ, отрезок FE
Сколько всего отрезков на данном чертеже?
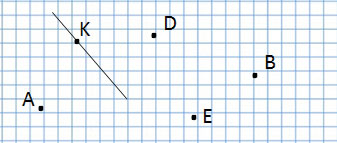
Ломаная линия
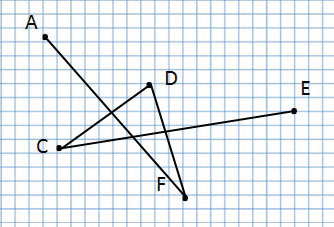
А эта ломаная линия совсем по-другому, потому что соединение точек у неё другое:
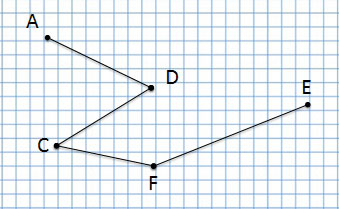
Ломаная линия ACDFE
Прочитаю название следующей ломаной линии:
Ломаная линия AFDCE
Многоугольники
Угол
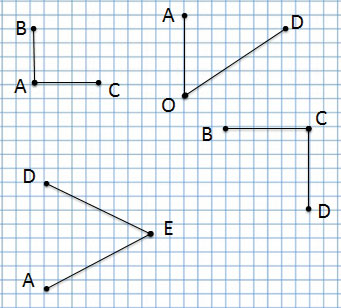
Угол обозначается тремя буквами. В середине указывается буква, которая обозначает вершину угла.
1 угол: угол BAC или CAB с вершиной А
2 угол: угол AOD или DOA с вершиной О
3 угол: угол AED или DEA с вершиной Е
4 угол: угол BCD или DCB с вершиной С
Поделись с друзьями в социальных сетях:
Геометрия. Урок 4. Четырехугольники
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Определение четырехугольника
Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Выпуклые четырехугольники
В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.
Диагонали выпуклого четырехугольника пересекаются в одной точке.
Площадь произвольного выпуклого четырехугольника можно найти по формуле:
S = 1 2 d 1 d 2 ⋅ sin φ
где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).
Рассмотрим более подробно некоторые виды выпуклых четырехугольников.
Класс параллелограммов : параллелограмм, ромб, прямоугольник, квадрат.
Класс трапеций : произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.
Параллелограмм
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
Свойства параллелограмма:
Площадь параллелограмма можно найти по трём формулам.
Как произведение стороны и высоты, проведенной к ней.
Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.
Как произведение двух смежных (соседних) сторон на синус угла между ними.
Как полупроизведение диагоналей на синус угла между ними.
Ромб – параллелограмм, у которого все стороны равны.
Свойства ромба:
Площадь ромба можно найти по трём формулам.
Как произведение стороны ромба на высоту ромба.
Как квадрат стороны ромба на синус угла между двумя сторонами.
Как полупроизведение диагоналей ромба.
Прямоугольник
Свойства прямоугольника:
Площадь прямоугольника можно найти по двум формулам:
Как произведение двух смежных (соседних) сторон прямоугольника.
Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.
Квадрат
Квадрат – прямоугольник, у которого все стороны равны.
Свойства квадрата:
Площадь квадрата можно вычислить по двум формулам:
Как квадрат стороны.
Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).
Трапеция
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.
Свойства трапеции:
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2
Площадь трапеции можно найти по двум формулам:
Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.
Как полупроизведение диагоналей на синус угла между ними.
Виды трапеций
Прямоугольная трапеция – трапеция, у которой два угла прямые.
Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.
Свойство равнобокой трапеции: углы при основании равны
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с четырехугольниками
1 класс. Математика. Четырёхугольник. Обозначение четырёхугольника
1 класс. Математика. Четырёхугольник. Обозначение четырёхугольника
Вопросы
Задай свой вопрос по этому материалу!
Поделись с друзьями
Комментарии преподавателя
Многоугольник – это фигура, у которой несколько вершин, несколько сторон, несколько углов.
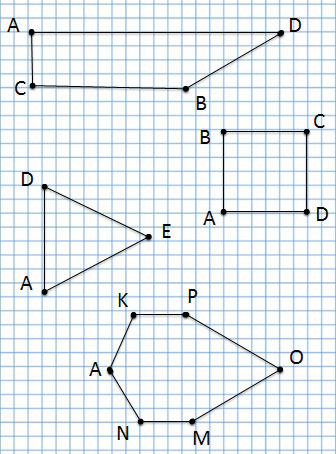
Задание 1. Разделить приведенные на Рис. 1 многоугольники на две группы.
Первая группа – группа треугольников
Треугольники – это фигуры, у которых 3 угла, 3 вершины и 3 стороны.
Вторая группа – группа многоугольников. Для определения их названия необходимо посчитать количество углов, сторон и вершин.
Итак, фигура, у которой 4 стороны, 4 угла и 4 вершины – это четырехугольник.
Каждому многоугольнику можно присвоить математическое имя при помощи латинских букв. Некоторые из них представлены на Рис. 4.
Для того чтобы назвать четырехугольник, достаточно у каждой из его вершин поставить по одной букве.
Пример 1: Присвоить имя многоугольнику.
Поставив латинскую букву у каждой из вершин многоугольника, мы получили четырехугольник ABCD.
Домашнее задание
1. Дайте математическое имя следующим четырехугольникам:
2. Сколько треугольников и четырехугольников изображено на рисунке?
Файлы
Нет дополнительных материалов для этого занятия.