ПРОЕКТ по предмету математика Тема: «Системы счисления»
Муниципальное бюджетное общеобразовательное учреждение
«средняя общеобразовательная школа № 8» с. Спасское
по предмету математика
Тема: «Системы счисления»
Автор: Ступник Дмитрий,
5 «А» класс
Руководитель: Лактионова М.П.,
2020 год
2. Теоретический материал
2.1. Из истории системы счисления.
2.2. Что такое система счисления?
2.3.Позиционные и непозиционные системы счисления.
2.4.Двоичная система счисления.
2.5.Шестидесятиричная система счисления.
2.6.Десятичная система счисления.
2.7.Другие системы счисления.
3.1. Опрос учеников 5-х классов 3.2.Результаты проведенного опроса
Современный человек в повседневной жизни постоянно сталкивается с числами и цифрами: запоминает номера автобусов и телефонов, в магазине подсчитывает стоимость покупок, ведет свой семейный бюджет и т.д. Числа и цифры с нами везде!
Искусство счета развивалось с развитием человечества. Способов счета было придумано немало. Какую же лучше использовать систему счисления в том или ином случае?
Цель: Узнать какая система счисления наиболее удобна.
Десятичная система счисления самая привычная и удобная.
— познакомить учащихся с возникновением и развитием системы счисления;
— дать представление о роли и назначении систем счисления;
— побудить интерес к изучению темы, с использованием информационно- коммуникационных технологий;
-найти и проанализировать научную литературу;
-отобрать нужный материал по данной теме;
-оформить работу;
Методы исследования: теоретический анализ, дедуктивный метод.
Планируемый результат: доказать, что десятичная система самая привычная и удобная.
2. Теоретический материал
2.1. Из истории системы счисления.
Современный человек в повседневной жизни постоянно сталкивается с числами: мы запоминаем номера автобусов и телефонов, в магазине подсчитываем стоимость покупок, ведём свой семейный бюджет в рублях и копейках (сотых долях рубля) и т.д. Числа, цифры. они с нами везде. А что знал человек о числах несколько тысяч лет назад? Вопрос непростой, но очень интересный. Историки доказали, что и пять тысяч лет назад люди могли записывать числа и производить над ними арифметические действия. Конечно, принципы записи были совсем не такими, как сейчас. Но в любом случае число изображалось с помощью одного или нескольких символов.
Эти символы, участвующие в записи числа, в математике принято называть цифрами
Но что же люди понимают тогда под словом «число»?
Первоначально понятие отвлечённого числа отсутствовало, число было «привязано» к тем конкретным предметам, которые пересчитывали. Отвлечённое понятие натурального числа появляется вместе с развитием письменности. Дробные же числа изобрели тогда, когда возникла необходимость производить измерения. Измерение, как известно, это сравнение с другой величиной того же рода, выбираемой в качестве эталона.
Эталон называется ещё единицей измерения. Понятно, что единица измерения не всегда укладывалась целое число раз в измеряемой величине. Отсюда и возникла практическая потребность ввести более «мелкие» числа, чем натуральные. Дальнейшее развитие понятия числа было обусловлено уже развитием математики.
Сегодня, для записи чисел человечество использует в основном десятичную систему счисления. А что такое система счисления?
2.2. Что такое система счисления?
Различные системы счисления, которые существовали раньше и которые используются в настоящее время, делятся на две группы: позиционные и непозиционные.
Наиболее совершенными являются позиционные системы счисления, т.е. системы записи чисел, в которых вклад каждой цифры в величину числа зависит от её положения (позиции) в последовательности цифр, изображающей число. Например, наша привычная десятичная система является позиционной: в числе 34 цифра 3 обозначает количество десятков и «вносит» в величину числа 30, а в числе 304 та же цифра 3 обозначает количество сотен и «вносит» в величину числа 300.
2.3. Позиционные и непозиционные системы счисления
Существуют позиционные и непозиционные системы счисления.
В непозиционных системах вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.
Единичная
Алфавит – один знак 1
Значение числа равно сумме всех единиц
Эта система счисления появилась в Древнем Риме. Первые двенадцать натуральных чисел в римской системе записываются так: I, II, III, IV, V, VI, VII, VIII, IX, X, XI, XII.
Примеры записи чисел XXVIII – 28, MCMXXXV – 1935. С этими числами очень трудно производить арифметические действия. По этой причине в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях – на циферблате часов, в ряде других случаев.
Алфавит – семь знаков I(1), V(5), X(10), L(50), C(100), D(500), M(1000)
Значение числа равно сумме больших чисел и разности малых чисел, предшествующих большим числам
Впервые идея позиционной системы счисления возникла в древнем Вавилоне, Индии и Китае.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения
Любая позиционная система счисления характеризуется своим основанием.
Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе.
За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д
Например, число сто три представляется в десятичной системе счисления в виде:
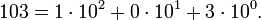
Наиболее употребляемыми в настоящее время позиционными системами являются:
10 — десятичная (используется повсеместно);
12 — двенадцатеричная (счёт дюжинами);
16 — шестнадцатеричная (в программировании, информатике )
60 — шестидесятеричная (единицы измерения времени).
Я расскажу о некоторых из них.
2.4.Двоичная система счисления
Двоичная система счисления – это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью двух символов: 1 и 0. Цифра двоичной системы — бит. Восемь цифр – байт.
Двоичная система счисления была придумана математиками и философами ещё в XVII-XIX веках. Выдающийся математик Лейбниц говорил: “Вычисление с помощью двоек…является для науки основным и порождает новые открытия… При сведении чисел к простейшим началам, каковы 0 и 1, везде появляется чудесный порядок”. Позже двоичная система была забыта, и только в 1936-1938 годах американский инженер и математик Клод Шеннон нашёл замечательное применение двоичной системы при конструировании электронных схем.
Таблица сложения в двоичной системе
Таблица умножения в двоичной системе
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой.
2.5.Шестидесятеричная система счисления
В современное время шестидесятеричная система счисления используется для измерения времени, углов.
В представлении времени используются три позиции: часы, минуты, секунды, так как для каждой позиции приходится использовать 60 цифр, а у нас только 10, то для каждой шестидесятеричной позиции используются две десятичные цифры (00, 01, …), позиции разделяются двоеточием. h:m:s.
Давайте решим две задачи:
Чтобы производить вычисления в шестидесятеричной системе счисления нужно знать таблицы сложения и умножения шестидесятеричных чисел. Каждая таблица очень большая, она размером 60*60, мы- то обычную таблицу умножения еле запомнили, а уж выучить шестидесятеричную таблицу нам будет ещё гораздо сложнее. Как же быть? Можно решать эти задачи в десятичной системе счисления, а потом результат перевести в шестидесятеричную.
45 минут=0*3600+45*60+0= 2700 секунд
2700*10=27000 секунд потребуется для выпечки 10 пирогов.
27000/60=450 (остаток 0)
7/60=0 (остаток 7) Получилось 07:30:00
2.6.Десятичная система счисления
Представление чисел с помощью арабских цифр – самая распространённая позиционная система счисления, она называется “десятичной системой счисления”. Десятичной она называется потому, что использует десять цифр: 0,1,2,3,4,5,6,7,8,9. Десятичная система счисления – наиболее известное достижение индийской математики (595год). Система с основанием 10 проникла по караванным путям из Индии во многие области Ближнего Востока. Постепенно эту систему всё шире стали применять в арабском мире, хотя одновременно в ходу оставались и другие системы. “Книга абака” Леонардо Пизанского (1202 год) была одним из источников для проникновения индийско-арабской системы нумерации в Западную Европу. Эта книга была грандиозным по тем временам трудом, в печатном виде она насчитывала 460 страниц. Её автор известен ещё и под именем Фибоначчи. Его книга представляла математическую энциклопедию своего времени. Десятичная система получила распространение и признание в Европе только в эпоху Возрождения.
2.7.Другие системы счисления
Пятеричная система счисления – Первые математики умели считать лишь по пальцам одной руки, а если предметов было больше, то говорили так: “пять +один” и т.д. Иногда за основу принимали число 20 – число пальцев на руках и ногах. Из 307 систем счисления первобытных американских народов 146 были десятичными, 106 – пятеричными и десятичными. Система с основанием 20 существовала у майя в Мексике и у кельтов в Европе.
3.1. Опрос учеников 5-х классов
Вопрос № 1: Знаете ли вы, что такое система счисления?
Вопрос № 2: Какие системы счисления вы знаете?
Вопрос № 3: Может ли человек отметить своё тысячелетие?
Вопрос № 4: Всегда ли 2+2=4?
Вопрос №5: Всегда ли 2*2 = 4
3.2.Результаты проведенного опроса
Системы исчисления в прошлом и настоящем (проект)
I. Введение
Цели и задачи проекта:
1. Изучить и сравнить древние и современные системы счисления.
2. Найти сходства и различия в древних и современных системах счисления.
3. Классифицировать системы счисления
Объекты исследования:
Древние и современные системы счисления
Методы:
1. Сравнительно-сопоставительный
2. Индукция.
3. Моделирование
4. Обобщение
5. Систематизация
6. Анкетирование
Объектом наших исследований стали системы счисления, которых оказалось гораздо больше, чем мы даже могли предположить. Стало очень интересно узнать о жизни предков и попробовать считать как они. По мере изучения выяснилось, что и в наши дни осталось достаточно много «воспоминаний» о канувших в лета системах счислений.
II. Основная часть
Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков.
1. Все начинается с пальцев
Существует много систем счисления и многие из них используются в разных областях до сих пор. Например, вы когда-то задумывались, почему люди используют именно десятичную систему счисления?
На ранних ступенях развития общества люди почти не умели считать. Они различали совокупности двух и трех предметов; всякая совокупность, содержавшая большее число предметов, объединялась в понятии «много». Предметы при счете сопоставлялись обычно с пальцами рук и ног. По мере развития цивилизации потребность человека в счете стала необходимой. Первоначально натуральные числа изображались с помощью некоторого количества черточек или палочек, затем для их изображения стали использовать буквы или специальные знаки. Ну а что может быть проще, чем собственные пальцы?
Таким образом, что вполне логично, существовали пятеричная и двадцатеричная системы счисления.
2. Пятеричная система счисления
По свидетельству известного исследователя Африки Стэнли, у ряда африканских племен была распространена пятеричная система счисления.
Долгое время пользовались пятеричной системой счисления и в Китае. Очевидна связь этой системы со строением человеческой руки. Также пятеричная система использовалась в Древнем Риме. Происхождение цифр явно связано со счетом с помощью тех же «подручных средств». Только здесь уже в ход пошли не только пальцы, а кисти рук полностью.
3. Двадцатеричная система счисления
Но совсем непростительно было бы не воспользоваться и остальными «счетными средствами».
Таким образом, у ацтеков и Майя была принята двадцатеричная система счисления за одним исключением: во втором разряде было не 20, а 18 ступеней, то есть за числом (17)(19) сразу следовало число (1)(0)(0). Это было сделано для облегчения расчётов календарного цикла, поскольку (1)(0)(0) = 360 примерно равно числу дней в солнечном году. Для записи основными знаками были точки(единицы) и отрезки(пятёрки).Также двадцатеричная система счисления была принята и у кельтов, населявших Западную Европу, начиная со второго тысячелетия до нашей эры. Основу для счета в этой системе составляли пальцы рук и ног. Некоторые следы двадцатеричной системы счисления кельтов сохранились во французской денежной системе: основная денежная единица – франк делится на 20 су.
4. Шестидесятеричная система счисления
Также нельзя не сказать о шестидесятеричной системе счисления.
Происхождение этой системы неясно. По одной гипотезе, она связана с применением двенадцатеричной системы счисления и счёта на пальцах (60 = 5 × 12, где 5 — число пальцев на руке).
Вавилонское государство также унаследовало шестидесятеричную систему и передало её, вместе с таблицами наблюдений за небом, греческим астрономам.
В более позднее время шестидесятеричная система использовалась арабами, а также древними и средневековыми астрономами, в первую очередь, для представления дробей. Поэтому средневековые учёные часто называли шестидесятеричные дроби «астрономическими». Эти дроби использовались для записи астрономических координат — углов, и эта традиция сохранилась по сей день. В одном градусе 60 минут и в одной минуте 60 секунд. Возможно, эта система взята не от человека, а от Солнца. По представлениям древних астрономов год состоял из 360=60×6 дней, то есть за одни сутки Солнце сдвигалось относительно звезд на 1/360 всего годового пути, а именно на 1 градус. Число 60 лежит и в основе более мелких угловых единиц: минут и секунд. Представление времени в виде количества суток, часов, минут и секунд: величина «d дней, h часов, m минут, s секунд» соответствует значению d×24×60×60+h×60×60+m×60+s секунд.
5. Двенадцатеричная система счисления
И, наконец, не менее интересная система счисления – двенадцатеричная. Она заслуживает особого внимания! Хотя бы потому, что ею пользовались купцы на Руси, исчисляя товар в дюжинах.
Как говорится, нет предела совершенству. Придумали тот же простой счет на пальцах, но с использованием лишь одной руки. Для этого использовались не пальцы обеих рук, а фаланги одной руки, а большой палец помогал считать, но сам в счет не входил.
Можно провести некоторую параллель между двенадцатеричной системой счисления и нашей, десятичной. В любой системе есть так называемые круглые числа. Итак, наш привычный десяток соответствует дюжине, то есть числу 12, сотня (10×10) соответствует следующему разряду десятичной системы, в двенадцатеричной он называется гроссу, наша тысяча соответствует следующему разряду – массе. Именно отсюда взялось выражение «У меня масса дел…». Здесь используется не физическая величина, а именно эта единица двенадцатеричной системы.
А знаком ли вам жест «чуть-чуть?». Он взялся именно из двенадцатеричной системы счисления. Это не что иное, как единица, то есть наименьшее число системы.
Ну и, раз уж дюжина так основательно вошла в обиход, появились и другие измерения с ее использованием.
Так как чуть ли не основным товаром купцов были шкурки пушных зверьков, именно для них и ввелись новые единицы.
1 резана=2дюжинам белей – шкурок горностая
1 куна=4 дюжинам белей
1 ногата=5 дюжинам белей
1 гривна=100 дюжинам белей
Элементы двенадцатеричной системы сохранились в Англии и по сей день. В системе мер 1 фут=12 дюймам. В денежной системе 1 шиллинг=12 пенсам. Нередко мы сталкиваемся с отголосками двенадцатеричной системы и в быту: сервиз на 12 персон, на циферблате часов 12 чисел, в году 12 месяцев, 12-летний цикл в названиях месяцев по китайскому календарю, и даже яйца за границей продают по 12 штук в отличие от наших десятков.
6. Алфавитные системы счисления
До сих пор речь шла о системах счисления, в которых использовались цифры. Но существовали также и другие. Для записи цифр использовали буквенные символы. Примеров можно привести несколько.
a. Славянская кириллическая
Начнем с нашей Родины. Древние славяне использовали для счета алфавитную систему счисления. Это значит, что вместо цифр они использовали буквы алфавита. Так «аз»-первая буква, означала единицу, «И»-десятая, означала десять, а буква «рцы»- двадцатая, означала сотню. Более крупные числа, тьма(обозначало 10 000) или миллион, выглядели следующим образом: к обычной цифре добавляли специальный знак, который обозначал тысячу.
b. Древнегреческая ионийская
На слайде перед вами древнегреческая ионийская десятеричная система счисления, которая возникла примерно в 3 тысячелетии до нашей эры. Она состоит из отдельных иероглифов: 1 (вертикальная палочка обозначавшая, мерную палку), 10 (напоминает путы для стреноживания коров), 100 (мерительная веревка), 1000 (цветок лотоса), 10 000 (указательный палец), 100 000 (лягушка), 1 000 000 (человек, поднявший вверх руки перед таким большим числом), 10 000 000 (Солнце или вся Вселенная). При записи числа иероглифы писались столько раз, сколько в этом числе единиц соответствующего разряда. Разряды писались справа налево (слева – меньшие, справа – большие) – в обратном порядке, чем у нас сейчас. Попробуйте сложить два больших числа, зная, что более 9 одинаковых иероглифов использовать нельзя, и вы сразу поймете, что для работы с этой системой нужен специальный человек. Это являлось недостатком такой системы счисления. Но, с другой стороны нас очень привлекла система знаков для обозначения чисел в Древнем Египте: они очень интересны, своеобразны, а также имеют интересную жизненную интерпретацию.
В дальнейшем эта система претерпела некоторые изменения. Она стала во многом аналогична с древнеславянской. Цифры изображаются с помощью букв, и сверху ставится специальная черточка.
c. Славянская глаголическая
7. Классификация систем счислений на позиционные и непозиционные
В наше время одновременно сосуществуют различные системы счисления: арабская, римская и многие другие. Все они принципиально делятся на позиционные и непозиционные.
а. Непозиционная система
Если в системе счисления позиция, на которой находится цифра, влияет на ее величину, то система, соответственно, позиционная. Примером непозиционной системы, помимо известной нам римской, может служить древнеегипетская десятичная, которая возникла во второй половине третьего тысячелетия до нашей эры, в ней использовались специальные цифры для обозначения чисел 1, 10, 102, 103, 104, 105, 106 и 107. Числа в египетской системе счисления записывались как комбинации этих цифр, в которых каждая из них повторялась не более девяти раз. На слайде представлен пример записи числа 345 на древнеегипетской системе счисления.
Непозиционные системы счисления имеют ряд существенных недостатков:
1.Существует постоянная потребность введения новых знаков для записи больших чисел,
2.Невозможно представлять дробные и отрицательные числа,
3.Сложно выполнять арифметические операции.
b. Позиционная система
Примером позиционной системы счисления может служить наша с вами система, в среде которой выполняются все наши операции.
Возникновение десятичной системы – это одно из самых важных событий в математике. Неудивительно, что история десятичной системы счисления занимает умы многих ученых. Существует несколько версий возникновения системы. Существует версия, что она зародилась в Китае. Есть также предположение, что ее изобрел Аль-Хорезми (узбекский математик). Но более распространенная версия состоит в том, что история возникновения десятичной системы началась в Индии. Сначала в этой системе счисления было всего девять цифр, ноль появился гораздо позднее.
Европейцы заимствовали систему у арабов, и назвали арабской. Это неправильное название сохранилось и до сих пор. Как ни странно, но сами арабы называют эти цифры индийскими. Первые записи десятичной системы счисления в Европе, найдены в испанских рукописях, которые датируются X веком. Но закрепилась она только в 12 в. Но эта система счисления была очень сложной, и первое время ей даже запрещали пользоваться. История десятичной системы счисления была очень долгой и непростой.
8. Системы счисления в информационных технологиях
Также актуальна тема систем счисления в сфере компьютерного мира и представления данных и кодировании информации. Здесь нашли применение 4 системы счисления: двоичная, восьмеричная, десятичная и шестнадцатеричная.
Основоположником двоичной системы является немецкий философ Лейбниц Готфрид Вильгельм. Двоичная система проста, так как для представления информации в ней используются всего два состояния или две цифры. Такое представление информации принято называть двоичным кодированием. Представление информации в двоичной системе использовалось человеком с давних времен. Так, жители островов Полинезии передавали необходимую информацию при помощи барабанов: чередование звонких и глухих ударов (на подобии азбуки Морзе).
С точки зрения технической реализации использование двоичной системы счисления для кодирования информации оказалось намного более простым, чем применение других способов. Действительно, удобно кодировать информацию в виде последовательности нулей и единиц: 0 – отсутствие электрического сигнала, 1 – наличие электрического сигнала.
Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
— для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток и нет тока, намагничен и не намагничен и т.п.), а не, например, с десятью, как в десятичной;
— представление информации посредством только двух состояний надежно и помехоустойчиво;
— двоичная арифметика намного проще десятичной.
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи. Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Для программистов удобнее работать с более компактной записью.
В итоге было решено использовать альтернативные и более простые системы счисления: восьмеричную и шестнадцатеричную. Числа 8 и 16 являются степенями двойки (2 в третьей и 2 в четвёртой степени соответственно), поэтому выполнять преобразования из двоичной системы и, наоборот, гораздо легче, чем при десятичной системе счисления, которая не может похвастаться своей причастностью к степеням числа 2.
Кроме того, числа в восьмеричной системе как минимум более приятны глазу и гораздо короче, чем их аналоги в двоичной системе.
Учитывая, что спокойно сосуществуют разные системы счисления, вполне логично предположить, что между ними есть связь. Перевести число из одной системы счисления в другую довольно просто. Чтобы перевести из привычной нам десятичной системы в другую надо всего лишь использовать известное нам с начальной школы деление «уголочком» или столбиком. А так как из десятичной переводят делением, то обратно, что вполне логично, переводят умножением.
III. Заключение
Работая над этим проектом, мы столкнулись с огромным количеством интересной информации. Мы бы хотели закончить наше выступление словами немецкого философа Готфрида Вильгельма Лейбница: «Кто хочет ограничиться настоящим, без знания прошлого, тот никогда его не поймет…»
Анкета соц.опроса. (было опрошено 30 человек)
1. Знаете ли вы, как считали на пальцах, когда счет велся не на десятки, а на дюжины?
2. Сколько это – дюжина?
3. Масса – это сколько?
4. Равно ли число, записанное в римской и в арабской системах счисления тремя единицами?
5. Лягушка – это сколько?
9. Список литературы.










