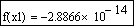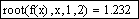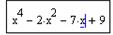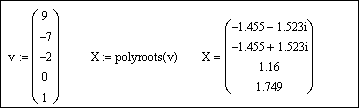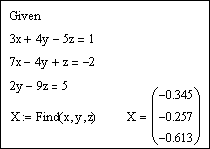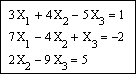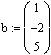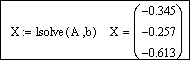Как написать систему уравнений в маткаде
Уравнение и системы уравнений в математическом пакете Mathcad в символьном виде решаются с использованием специального оператора символьного решения solve в сочетании со знаком символьного равенства, который может быть также введен с рабочей панели “Символика”. Например:
Аналогичные действия при решении уравнений в Mathcad можно выполнить, используя меню “Символика”. Для этого необходимо записать вычисляемое выражение. Затем выделить переменную, относительно которой решается уравнение, войти в меню Символика, Переменная, Разрешить. Например:
В случае, если необходимо упростить полученный результат, используется знак равенства [=]. Например:
При решении некоторых уравнений, результат включает большое количество символов. Mathcad сохраняет его в буфере, а на дисплей выводитcя сообщение: “This array has more elements than can be displayed at one time. Try using the “submatrix” function” – “Этот массив содержит больше элементов, чем может быть отображено одновременно. Попытайтесь использовать функцию “submatrix””. В этом случае рекомендуется использовать численное решение. Или, в случае необходимости, символьное решение может быть выведено и отображено на дисплее.
Символьное решение может быть получено с использованием блока given … find. В этом случае при записи уравнения для связи его левой и правой части использует символ логического равенства “=” с панели инструментов Boolean, например:
Аналогичным способом решаются системы уравнений в символьном виде. Ниже приводятся примеры решения систем уравнений в символьном виде различными способами. При использовании оператора символьного решения solve в сочетании со знаком символьного равенства 
система уравнений должна быть задана в виде вектора, который вводится вместо левого маркера оператора solve, а перечень переменных, относительно которых решается система, вместо правого маркера. Например:
Пример использования блока given…find для решения системы уравнений:
23. Тема 6. Решение уравнений и систем. Краткие теоретические сведения
Для алгебраических уравнений вида F(x)=0 решение в MathCad находится с помощью функции Root.
Общий вид функции следующий:
F(х) – функция, описывающая левую часть выражения вида F(x)=0,
Х – имя переменной, относительно которой решается уравнение.
Функция позволяет найти как вещественные корни, так и комплексные. В случае комплексного корня начальное приближение нужно задать в виде комплексного числа.
Если после многих итераций Mathcad не находит подходящего приближения, то появится сообщение «отсутствует сходимость».
Эта ошибка может быть вызвана следующими причинами:
· уравнение не имеет корней;
· корни уравнения расположены далеко от начального приближения;
· выражение F(x) имеет разрывы между начальным приближением и корнем;
· выражение имеет комплексный корень, но начальное приближение было вещественным и наоборот.
Для изменения точности, с которой функция Root ищет корень, нужно изменить значение системной переменной TOL. Например, просле задания в документе оператора TOL:=0.00001 точность вычисления корня станет равной 0.00001.
Для нахождения корней полиномиального уравнения вида
В отличие от функции Root, Polyroots не требует начального приближения и вычисляет сразу все корни, как вещественные, так и комплексные.
Функция вычисляет вектор длины N, состоящий из корней полинома.
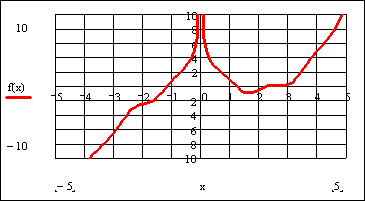
На рисунке 2.6.1 приведены примеры вычисления корней уравнений с помощью функций Root и Polyroots.
Рисунок 2.6.1 – Примеры решения уравнений
MathCAD дает возможность решать системы уравнений и неравенств.
Наиболее распространенным методом решения уравнений в Mathcad является блочный метод. Для решения системы этим методом необходимо выполнить следующее:
A) задать начальное приближение для всех неизвестных, входящих в систему уравнений;
Б) задать ключевое слово Given, которое указывает, что далее следует система уравнений;
В) ввести уравнения и неравенства в любом порядке (использовать кнопку логического равенства на панели знаков логических операций 
Для набора знака «=» в уравнении);
Г) ввести любое выражение, которое включает функцию Find.
Решающим блоком называется часть документа, расположенная между ключевыми словами Given и Find.
После набора решающего блока Mathcad возвращает точное решение уравнения или системы уравнений.
Обратиться к функции Find можно несколькими способами:
X := Find(x1, x2,…) – формируется переменная или вектор, содержащий вычисленные значения корней.
Сообщение об ошибке «Решение не найдено» появляется тогда, когда система не имеет решения или для уравнения, которое не имеет вещественных корней, в качестве начального приближения взято вещественное число и наоборот.
Приближенное решение уравнения или системы можно получить с помощью функции Minerr.
Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке. Правила использования функции Minerr такие же, как и для функции Find. Часть документа, расположенная между ключевыми словами Given и Minerr так же носит название решающего блока.
Примеры решения систем уравнений с помощью решающего блока приведены на рисунке 2.6.2.
Для решения систем линейных уравнений можно использовать общепринятые математические методы: метод Крамера, матричный метод и т. д.
Матричный метод решения системы линейных уравнений реализован в функции Lsolve. Общий вид функции:
Где А – матрица коэффициентов перед неизвестными, B – вектор свободных членов.
Матричный метод можно реализовать и с помощью обратной матрицы. Примеры решения систем линейных уравнений с помощью матричного метода приведены на рисунке 2.6.2.
Рисунок 2.6.2 – Примеры решения систем уравнений
Из рисунка 6.2 видно, что при решении системы уравнений блочным методом можно получить численные значения корней системы уравнений, без присваивания и с присваиванием их в переменные x1 и x2. При решении системы уравнений матричным методом продемонстрированы два варианта: с использованием стандартной функции Lsolve и обратной матрицы.
Как написать систему уравнений в маткаде
Глава 4. Решение уравнений
4.4 Решение систем уравнений
Для решения систем уравнений нужно использовать вычислительный блок следующего вида:
1. Начальные приближения для всех переменных.
2. Ключевое слово Given (Дано).
3. Система уравнений (при записи уравнений надо использовать жирный знак равенства– клавиши Ctrl +=, так как это не знак присвоения значения, а оператор отношения).
4. Ограничения на поиск решения в виде неравенств, если они есть.
Результат расчета – вектор решения системы. Вычислительный блок позволяет решать системы, содержащие от 1 до 200 уравнений.
начальное приближение
Given 
проверка 
Рис. 4. 9 Решение системы уравнений с помощью функции Find
– Linear (Линейный метод) – метод касательной;
– Nonlinear (Нелинейный метод);
– Quadratic (Квадратичный метод).
Нелинейных методов три:
1) Conjiugate Gradient (Метод сопряженных градиентов);
2) Quasi – Newton (Квази – ньютоновский метод);
3) Levenberg – Marquart (Метод Левенберга).
Кроме выбора самого метода, нажав кнопку Advanced Options (Дополнительные параметры), можно выбрать:
1) оценку производной конечными разностями ( Derivate Estimation ):
– Forward (Вперед) – правая двухточечная схема;
– Central (Центральная) – трехточечная симметричная схема;
2) оценку переменной ( Variable Estimation ):
– Tangent (Касательная) – касательная – прямая линия,
– Quadratic (Квадратичная) – касательная – парабола;
3) проверку линейности:
начальные приближения
Given 
один из параметров делаем константой, другой варьируем
для графика
для таблицы
Рис. 4. 10 Решение системы уравнений с переменными параметрами
Меняем оба параметра a и b
Диапазон изменения координат a и b задан на странице
Quick Plot Data окна форматирования
Рис. 4. 11 поверхность решений системы уравнений
Mathcad позволяет решать системы уравнений не только в скалярной, но и в матричной форме, при этом начальные условия и ограничения задаются в виде векторов (рис. 4.12).
Решение системы алгебраических линейных уравнений
А*Х=В путем обращения матрицы А
начальное приближение 
Given 
Функция root с матрицами работать не может
Рис. 4. 12 Решение системы уравнений в матричном виде
Как написать систему уравнений в маткаде
РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ
4 Решение уравнений и систем средствами Mathcad
Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.
Функция root, блоки Given…Find, Given…Minerr
В ходе численного решения обычно выделяют два этапа:
Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается
root(f(x), x, [a, b])
и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:
Этот прием используется в Mathcad так:
Кроме того, пакет Mathcad имеет встроенную функцию
lsolve(A, b),
Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.
Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.
Порядок выполнения лабораторной работы
Лабораторная работа № 4
Решение уравнений и систем в Mathcad.
Задание 1. Решить уравнение 
.
Решение.
Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.
Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:
Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:
Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика 
сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).
Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).
Для появления графика щелкнем левой клавишей мыши вне графической области.
Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.
Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.
После указанных преобразований график функции f(x) будет выглядеть следующим образом:
Этап отделения корней завершен.
Уточним теперь корни уравнения с помощью функции root.
Присвоим начальное приближение переменной x и укажем точность поиска корня:
Уточним заданное приближение к значению корня с помощью функции root:
Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:
Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:
Задание 2. Решить уравнение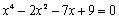 
.
Решение.
Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:
Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать 
на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.
Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить 
на панели инструментов или комбинацию клавиш Ctrl + V.
Для получения результата напечатаем polyroots(v) =:
Задание 3. Решить систему линейных уравнений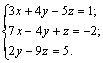 
Сделать проверку.
Решение.
1-й способ. Использование блока Given … Find.
Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:
Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).
После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:
Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом
После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.
2-й способ. Использование блока Given…Minerr.
Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:
3-й способ. Решение системы линейных уравнений матричным способом.
Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:
Решим систему матричным способом по формуле
Решим систему с помощью функции lsolve:
Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:
Категории
Mathcad системы уравнений
Программа Mathcad предоставляет возможность численного и символьного решения систем уравнений. Один из популярных методов решения систем уравнения в Mathcad это метод с использованием команд Given и Find. Давайте подробнее разберем как это сделать.
Численное решение систем уравнений в Mathcad
Для примера рассмотрим задачу:
mathcad система уравнений
Как видим, правильный ответ будет под номером 4.
Символьное решение систем уравнений в Mathcad
Чтобы решить систему уравнений символьно, будем использовать те же операторы, только будут кое-какие различия в воде. Т.к. нам не нужно конкретное значение, то и начальные значения переменных вводить не нужно. Возьмем для рассмотрения пример:
