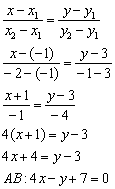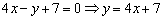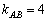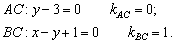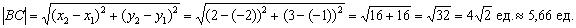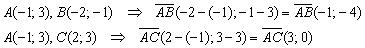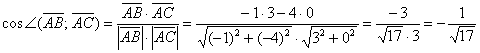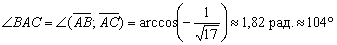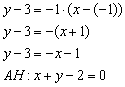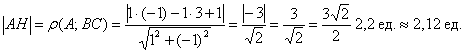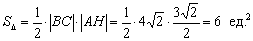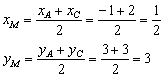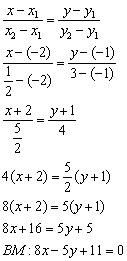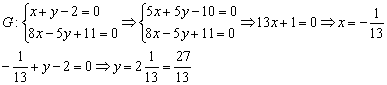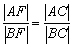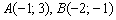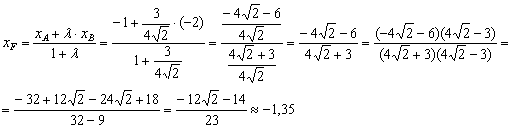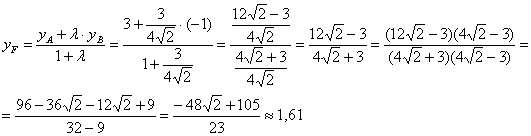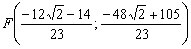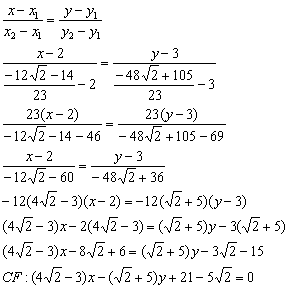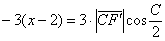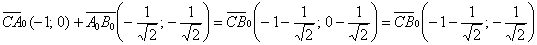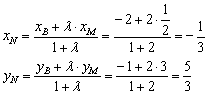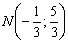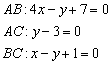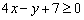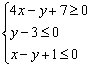Слово Как написать уравнение высоты треугольника по координатам вершин - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Источник

Уравнение высоты треугольника в пространстве

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Что ты хочешь узнать?

Ответ

Проверено экспертом

Высоты треугольника пересекаются в одной точке.

Следовательно, достаточно найти уравнения двух любых высот треугольника и точку их пересечения, решив систему двух уравнений.

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Значит надо найти уравнение стороны треугольника и уравнение прямой, проходящей через противоположную вершину, перпендикулярно этой стороне.

Уравнение прямой АВ найдем по формуле:

(X+4)/2=(Y-0)/-2 – каноническое уравнение =>

y=-x-2 – уравнение прямой с угловым коэффициентом k=-1.

Условие перпендикулярности прямых: k1=-1/k => k1=1.

Тогда уравнение перпендикуляра к стороне АВ из вершины С

y=х (1) – это уравнение перпендикуляра СС1.

Уравнение прямой АС:

(X+4)/6=(Y-0)/2 – каноническое уравнение =>

y=(1/3)x+4/3 – уравнение прямой с угловым коэффициентом k=1/3.

Тогда уравнение перпендикуляра к стороне АС из вершины В

Y-Yb=k1(X-Xb) или Y+2=-3(X+2) =>

y=-3х-8 (2)- это уравнение перпендикуляра BB1.

Точка пересечения перпендикуляров имеет координаты:

Ответ: точка пересечения высот совпадает с вершиной В(-2;-2)

треугольника, то есть треугольник прямоугольный с

Дан треугольник ABC, где

внутренний угол A с точностью до градуса;

уравнение и длину высоты, опущенной из вершины C;

точку пересечения высот;

уравнение медианы, проведенной через вершину C;

систему линейных неравенств, определяющих треугольник ABC;

треугольник угол высота медиана

Расстояние d между двумя точками

Расстояние d между двумя точками и определяется по формуле

Применяя (1), находим длину стороны АВ:

Внутренний угол A с точностью до градуса

Тогда искомый угол находим по его косинусу:

A = arccos (-0,3165) = 108,4 o

Уравнение и длину высоты, опущенной из вершины C

Находим уравнение стороны АВ по формуле прямой проходящей через две точки:

Уравнение прямой проходящей через точки A (x a, y a) и B (x b, y b) в общем виде:

Отсюда следует, что уравнение АВ можно записать в виде: Её угловой коэффициент Тогда угловой коэффициент высоты, опущенной из вершины C а уравнение высоты то есть, 3 x – 4 y – 36 = 0 – уравнение высоты CH.

Длина высоты есть расстояние от точки С до прямой АВ: 4 x + 3 y – 8 = 0; A=4; B=3:

Точка пересечения высот

Аналогично найдем уравнение высоты АМ.

Находим уравнение стороны АВ по формуле прямой проходящей через две точки:

Уравнение прямой проходящей через точки C (x c, y c) и B (x b, y b) в общем виде:

Отсюда 2 x – y – 14 = 0 – уравнение высоты AM

Точку пересечения высот К находим, решая систему уравнений:

Решая системы методом исключения, получаем K(4;-6).

Уравнение медианы, проведенной через вершину C

Находим середину стороны АВ,

применяя формулы деления отрезка на две равные части:

Подставив в (1) координаты точек С и Е, находим уравнение медианы:

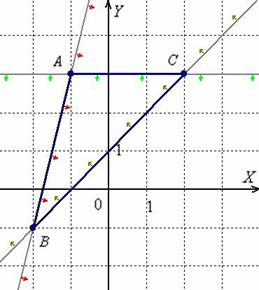
Cистема линейных неравенств, определяющих треугольник ABC

Выпишем уравнения сторон треугольника:

4 x + 3 y – 8 = 0 – уравнение прямой AB.

x – 3 y – 17 = 0 – уравнение прямой AC.

x + 2 y – 2 = 0 – уравнение прямой BС.

Тогда система линейных неравенств, определяющих треугольник ABC, имеет вид:

Источник

Прямая на плоскости. Примеры решений

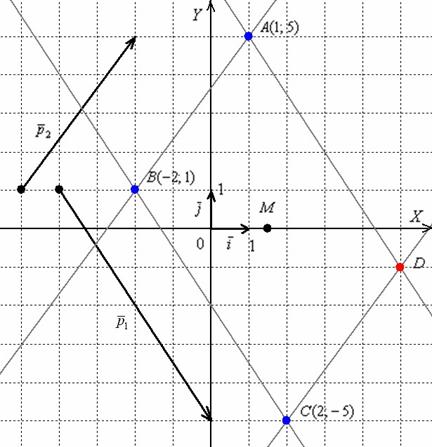
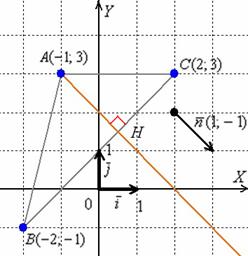
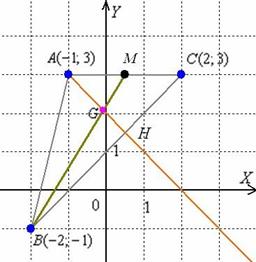
Пример. Даны координаты вершин треугольника АВС: А(–3; –1), В(4; 6), С(8; –2).
Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

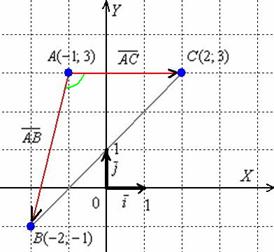
Пример №3. Даны вершины A(1;1), B(7;4), C(4;5) треугольника. Найти: 1) длину стороны AB ; 2) внутренний угол A в радианах с точностью до 0,001. Сделать чертеж.
Скачать

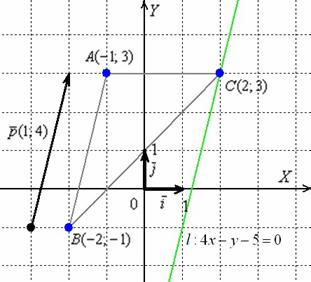
Пример №4. Даны вершины A(1;1), B(7;4), C(4;5) треугольника. Найти: 1) уравнение высоты, проведенной через вершину C ; 2) уравнение медианы, проведенной через вершину C ; 3) точку пересечения высот треугольника; 4) длину высоты, опущенной из вершины C. Сделать чертеж.
Скачать

Задание. По координатам вершин пирамиды А1,А2,А3,А4 найти: 1) длины ребер А1А2 и А1А3; 2) угол между ребрами А1А2 и А1А3; 3) площадь грани А1А2А3;4) объем пирамиды А1А2А3А4
A₁(3;5;4,0,0), A₂(8;7;4,0,0), A₃(5;10;4,0,0), A₄(4;7;9,0,0):Пример №10

Пример. В декартовой прямоугольной системе координат даны вершины пирамиды A, B, C, D. Найдите длину ребра AB, косинус угла между векторами, уравнение ребра, уравнение грани, уравнение высоты.
Решение

Источник

Как научиться решать задачи по аналитической геометрии?
Типовая задача с треугольником на плоскости

Этот урок создан на подходе к экватору между геометрией плоскости и геометрией пространства. В данный момент назрела необходимость систематизировать наработанную информацию и ответить на очень важный вопрос: как научиться решать задачи по аналитической геометрии? Трудность состоит в том, что задач по геометрии можно придумать бесконечно много, и никакой учебник не вместит в себя всё множество и разнообразие примеров. Это не производная функции с пятью правилами дифференцирования, таблицей и несколькими техническими приёмами….

Решение есть! Не буду говорить громких слов о том, что я разработал какую-то грандиозную методику, однако, по моему мнению, существует эффективный подход к рассматриваемой проблеме, позволяющий достигнуть хорошей и отличной результативности даже полному чайнику. По крайне мере, общий алгоритм решения геометрических задач очень чётко оформился в моей голове.

ЧТО НЕОБХОДИМО знать и уметь
для успешного решения задач по геометрии?

От этого никуда не деться – чтобы наугад не тыкать носом кнопки, требуется освоить азы аналитической геометрии. Поэтому если вы только-только приступили к изучению геометрии или капитально позабыли её, пожалуйста, начните с урока Векторы для чайников. Кроме векторов и действий с ними, нужно знать базовые понятия геометрии плоскости, в частности, уравнение прямой на плоскости и простейшие задачи с прямой на плоскости. Геометрия пространства представлена статьями Уравнение плоскости, Уравнения прямой в пространстве, Основные задачи на прямую и плоскость и некоторыми другими уроками. Кривые линии и пространственные поверхности второго порядка стоЯт некоторым особняком, и специфических задач с ними не так уж много.

Предположим, студент уже обладает элементарными знаниями и навыками решения простейших задач аналитической геометрии. Но вот бывает же так: читаешь условие задачи, и… хочется вообще закрыть всё это дело, закинуть в дальний угол и забыть, как о страшном сне. Причём это принципиально не зависит от уровня вашей квалификации, сам время от времени сталкиваюсь с заданиями, у которых решение не очевидно. Как поступать в таких случаях? Не нужно бояться задачи, которая вам не понятна!

Во-первых, следует установить – это «плоская» или пространственная задача? Например, если в условии фигурируют векторы с двумя координатами, то, понятно, тут геометрия плоскости. А если преподаватель загрузил благодарного слушателя пирамидой, то здесь явно геометрия пространства. Результаты первого шага уже неплохи, ведь удалось отсечь громадное количество ненужной для данной задачи информации!

Второе. Условие, как правило, озаботит вас некоторой геометрической фигурой. Действительно, пройдитесь по коридорам родного ВУЗа, и вы увидите очень много озабоченных лиц.

В «плоских» задачах, не говоря о разумеющихся точках и прямых, наиболее популярная фигура – треугольник. Его мы разберём очень подробно. Далее идёт параллелограмм, и значительно реже встречаются прямоугольник, квадрат, ромб, окружность, др. фигуры.

В пространственных задачах могут летать те же плоские фигуры + сами плоскости и распространённые треугольные пирамиды с параллелепипедами.

Вопрос второй – всё ли вы знаете о данной фигуре? Предположим, в условии идёт речь о равнобедренном треугольнике, а вы весьма смутно помните, что это такой за треугольник. Открываем школьный учебник и читаем про равнобедренный треугольник. Что делать… врач сказал ромб, значит, ромб. Аналитическая геометрия аналитической геометрией, но задачу помогут решить геометрические свойства самих фигур, известные нам из школьной программы. Если не знать, чему равна сумма углов треугольника, то мучиться можно долго.

Третье. ВСЕГДА старайтесь выполнять чертёж (на черновике/чистовике/мысленно), даже если этого не требуется по условию. В «плоских» задачах сам Евклид велел взять в руки линейку с карандашом – и не только для того, чтобы понять условие, но и в целях самопроверки. При этом наиболее удобный масштаб 1 единица = 1 см (2 тетрадные клетки). Уж не будем рассуждать о нерадивых студентах и вращающихся в гробах математиках – в таких задачах совершить ошибку практически невозможно. Для пространственных заданий выполняем схематический рисунок, который тоже поможет проанализировать условие.

Чертёж или схематический чертёж зачастую сразу позволяет увидеть путь решения задачи. Конечно, для этого нужно знать фундамент геометрии и рубить в свойствах геометрических фигур (см. предыдущий пункт).

Четвёртое. Разработка алгоритма решения. Многие задачи геометрии являются многоходовыми, поэтому решение и его оформление очень удобно разбивать на пункты. Нередко алгоритм сразу же приходит в голову, после того как вы прочитали условие или выполнили чертёж. В случае возникновения трудностей начинаем с ВОПРОСА задачи. Например, по условию «требуется построить прямую…». Здесь самый логичный вопрос такой: «А что достаточно знать, чтобы построить данную прямую?». Предположим, «точка нам известна, нужно знать направляющий вектор». Задаём следующий вопрос: «Как найти этот направляющий вектор? Откуда?» и т.д.

Иногда случается «затык» – не решается задача и всё тут. Причины стопора могут быть следующими:

– Серьёзный пробел в элементарных знаниях. Иными словами, вы не знаете или (и) не видите какой-то очень простой вещи.

– Незнание свойств геометрических фигур.

– Задача попалась трудная. Да, так бывает. Нет смысла часами париться и собирать слёзки в платочек. Обратитесь за консультацией к преподавателю, сокурсникам или задайте вопрос на форуме. Причём, его постановку лучше сделать конкретной – о том участке решения, который вам не понятен. Клич в виде «Как решить задачу?» выглядит не очень-то… и, прежде всего, для вашей собственной репутации.

Этап пятый. Решаем-проверяем, решаем-проверяем, решаем-проверяем-даём ответ. Каждый пункт задачи выгодно проверять сразу после его выполнения. Это поможет немедленно обнаружить ошибку. Естественно, никто не запрещает быстренько прорешать задачу целиком, но возникает риск переписывать всё заново (часто несколько страниц).

Вот, пожалуй, все основные соображения, которыми целесообразно руководствоваться при решении задач.

Практическая часть урока представлена геометрией на плоскости. Примеров будет всего два, но мало не покажется =)

Пройдёмся по нити алгоритма, который я только что рассмотрел в своём маленьком научном труде:

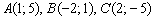
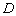
Даны три вершины параллелограмма . Найти вершину .

Шаг первый: очевидно, что речь идёт о «плоской» задаче.

Шаг второй: в задаче речь идёт о параллелограмме. Все помнят такую фигуру параллелограмм? Не нужно улыбаться, немало людей получает образование в 30-40-50 и более лет, поэтому даже простые факты могут стереться из памяти. Определение параллелограмма встречается в Примере № 3 урока Линейная (не) зависимость векторов. Базис векторов.

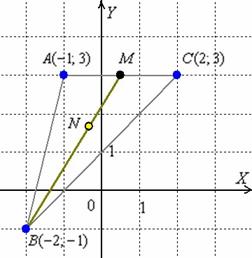
Шаг третий: Выполним чертёж, на котором отметим три известные вершины. Забавно, что несложно сразу построить искомую точку :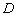

Построить, это, конечно, хорошо, но решение необходимо оформить аналитически.

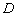
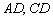
Шаг четвёртый: Разработка алгоритма решения. Первое, что приходит в голову – точку можно найти как пересечение прямых . Их уравнения нам неизвестны, поэтому придётся заняться этим вопросом:

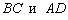
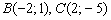
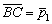
1) Противоположные стороны параллельны. По точкам найдём направляющий вектор данных сторон . Это простейшая задача, которая рассматривалась на уроке Векторы для чайников.

Примечание: корректнее говорить «уравнение прямой, содержащей сторону», но здесь и далее для краткости я буду использовать словосочетания «уравнение стороны», «направляющий вектор стороны» и т.д.

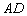
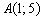
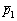
2) Составим уравнение прямой по известной точке и найденному направляющему вектору (см. статью Уравнение прямой на плоскости)

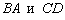
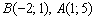
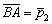
3) Противоположные стороны параллельны. По точкам найдём направляющий вектор этих сторон .

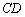
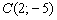
4) Составим уравнение прямой по точке и направляющему вектору

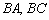
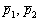
В пунктах 1-2 и 3-4 мы фактически дважды решили одну и ту же задачу, она, кстати, разобрана в примере № 3 урока Простейшие задачи с прямой на плоскости. Можно было пойти более длинным путём – сначала найти уравнения прямых и только потом «вытащить» из них направляющие векторы .

5) Теперь уравнения прямых 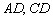известны. Осталось составить и решить соответствующую систему линейных уравнений (см. примеры № 4, 5 того же урока Простейшие задачи с прямой на плоскости).

Точка 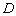найдена.

Задача довольно таки простая и её решение очевидно, но существует более короткий путь!

Второй способ решения:

Диагонали параллелограмма своей точкой пересечения делятся пополам. Точку 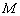я отметил, но чтобы не загромождать чертёж сами диагонали не провёл.

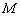
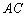
1) С помощью формул координат середины отрезка найдём точку – середину диагонали .

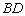
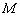
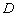
2) Рассмотрим диагональ . Из условия известна вершина «бэ», из предыдущего пункта найдена середина . Используя те же формулы координат середины отрезка, находим вершину .

Хорошее знание свойств параллелограмма позволило значительно сократить решение!

Желающие могут прорешать задачу. Всё перед глазами, все ссылки, комментарии даны. И, конечно, не забывайте про важный технический приём – решили пункт задания и сразу же его проверили (аналитически или по чертежу).

Переходим к наиболее распространённой задаче, которая встречается практически в каждом сборнике, в каждой методичке:

Типовая задача с треугольником на плоскости

Многие помнят из школы признаки равенства треугольников, признаки подобия треугольников и мучительное заучивание доказательств теорем. Как в сердцАх сказал один мой одноклассник, «не понимаю, на… доказывать равенство треугольников, если и так видно, что они одинаковые». Мы тоже не будем ничего доказывать, поскольку аналитическая геометрия подкрадывается к треугольнику совсем с другой стороны.

Типовая задача с треугольником на плоскости, как правило, формулируется так: Даны три вершины треугольника. Требуется найти… много чего требуется найти…. Повезёт, если будет пункта 3-4, но чаще всего их 5-6 и даже больше.

Даны вершины треугольника 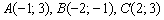. Требуется:

1) составить уравнения сторон 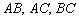и найти их угловые коэффициенты;
2) найти длину стороны ;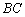
3) найти ;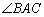
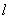
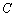
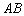
4) составить уравнение прямой , проходящей через точку параллельно прямой ;
5) составить уравнение высоты 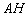и найти её длину;
6) вычислить площадь треугольника ;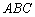
7) составить уравнение медианы ;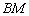
8) найти точку пересечения .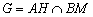

Знаете, прямо почувствовал себя палачом с большим топором. Чтобы не было так стыдно, скажу, что на практике в большинстве случаев пунктов бывает меньше. Просто я постарался собрать в одной задаче всё, что может встретиться. Для особо опасных энтузиастов заготовлена виселица ещё тройка пунктов, но это на закуску.

…бррр, что-то у меня сегодня траурная тема пошла, не иначе, от убыли светового дня. Поэтому скорее перехожу к решению.

Решение: С чего начать? Начать целесообразно с выполнения чертежа. По условию этого можно не делать, но для самоконтроля и самопроверки всегда строим чертёж на черновике.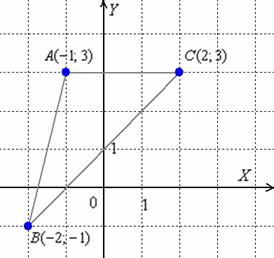

Ещё раз напоминаю, что самый выгодный масштаб 1 единица = 1 см (2 тетрадные клетки).

Поехали щёлкать орехи:

1) Составим уравнения сторон 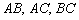и найдём их угловые коэффициенты.

Поскольку известны вершины треугольника, то уравнения каждой стороны составим по двум точкам. Процесс подробно рассмотрен на уроке Уравнение прямой на плоскости.

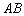
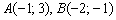
Составим уравнение стороны по точкам :

Для проверки следует мысленно либо на черновике подставить координаты каждой точки в полученное уравнение. Теперь найдём угловой коэффициент. Для этого перепишем общее уравнение в виде уравнения с угловым коэффициентом:

Таким образом, угловой коэффициент:

Аналогично находим уравнения сторон 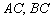. Не вижу особого смысла расписывать то же самое, поэтому сразу приведу готовый результат:

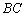
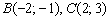
2) Найдём длину стороны . Это простейшая задача, рассмотренная на уроке Векторы для чайников. Для точек используем формулу:

По этой же формуле легко найти и длины других сторон. Проверка очень быстро выполнятся обычной линейкой.

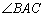
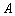
3) Найдём . Это угол при вершине . Есть несколько способов решения, но самый универсальный способ – находить угол при вершине, как угол между векторами. Данная задача подробно рассмотрена на уроке Скалярное произведение векторов.

Используем формулу .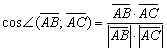

Найдём векторы:

Таким образом:

Кстати, попутно мы нашли длины сторон .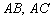

В результате:

Ну что же, похоже на правду, для убедительности к углу можно приложить транспортир.

Внимание! Не путайте угол треугольника с углом между прямыми. Угол треугольника может быть тупым, а угол между прямыми – нет (см. последний параграф статьи Простейшие задачи с прямой на плоскости). Однако для нахождения угла треугольника можно использовать и формулы вышеуказанного урока, но шероховатость состоит в том, что те формулы всегда дают острый угол. С их помощью я прорешал на черновике данную задачу и получил результат 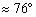. 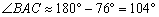А на чистовике пришлось бы записывать дополнительные оправдания, что .

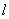
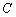
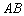
4) Составить уравнение прямой , проходящей через точку параллельно прямой .

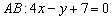
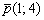
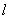
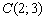
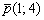
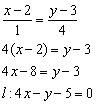
Стандартная задача, подробно рассмотренная в примере № 2 урока Простейшие задачи с прямой на плоскости. Из общего уравнения прямой вытащим направляющий вектор . Составим уравнение прямой по точке и направляющему вектору :

Как найти высоту треугольника?

5) Составим уравнение высоты 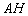и найдём её длину.

От строгих определений никуда не деться, поэтому придётся приворовывать из школьного учебника:

Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

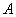
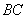
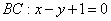
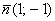
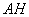
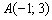
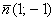
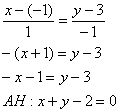
То есть, необходимо составить уравнение перпендикуляра, проведённого из вершины к стороне . Данная задача рассмотрена в примерах № 6, 7 урока Простейшие задачи с прямой на плоскости. Из уравнения снимаем вектор нормали . Уравнение высоты составим по точке и направляющему вектору :

Обратите внимание, что координаты точки 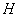нам не известны.

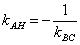
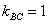
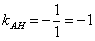
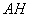
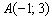
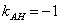
Иногда уравнение высоты находят из соотношения угловых коэффициентов перпендикулярных прямых: . В данном случае , тогда: . Уравнение высоты составим по точке и угловому коэффициенту (см. начало урока Уравнение прямой на плоскости):

Длину высоты можно найти двумя способами.

Существует окольный путь:

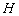
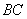
а) находим – точку пересечения высоты и стороны ;
б) находим длину отрезка 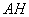по двум известным точкам.

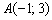
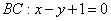
Но на уроке Простейшие задачи с прямой на плоскости рассматривалась удобная формула расстояния от точки до прямой. Точка известна: , уравнение прямой тоже известно: , Таким образом:

6) Вычислим площадь треугольника. В пространстве площадь треугольника традиционно рассчитывается с помощью векторного произведения векторов, но здесь дан треугольник на плоскости. Используем школьную формулу:
– площадь треугольника равна половине произведения его основания на высоту.

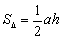
В данном случае:

Как найти медиану треугольника?

7) Составим уравнение медианы .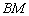

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

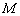
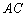
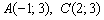
а) Найдём точку – середину стороны . Используем формулы координат середины отрезка. Известны координаты концов отрезка: , тогда координаты середины:

Таким образом: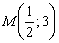

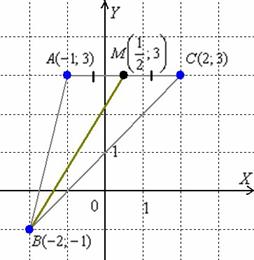
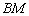
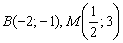
Уравнение медианы составим по точкам :

Чтобы проверить уравнение, в него нужно подставить координаты точек .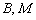

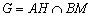
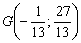
8) Найдём точку пересечения высоты и медианы. Думаю, этот элемент фигурного катания все уже научились выполнять без падений:

Любители строгого оформления могут записать сакраментальное слово «Ответ» и скрупулезно перечислить в 8 пунктах полученные результаты.

А сейчас рассмотрим более редкие задания. Треугольник тот же.

9) найти уравнение биссектрисы ;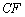
10) найти центр тяжести 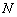треугольника;
11) составить систему линейных неравенств, определяющих треугольник.

Как найти уравнение биссектрисы треугольника?

9) Биссектриса – это луч, который делит угол пополам. Рассмотрим три способа решения этого пункта. Длинный. Покороче. И самый простой.

Способ первый. Чтобы были более понятны последующие выкладки, я сразу приведу готовый чертёж с результатом: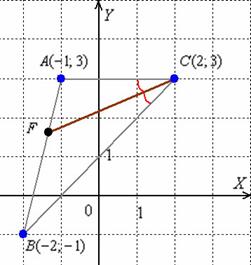

Из свойств биссектрисы внутреннего угла следует соотношение длин следующих отрезков:

Длины сторон уже найдены в предыдущих пунктах: .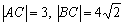

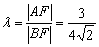
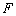
Таким образом: . Координаты точки найдём по формулам деления отрезка в данном отношении. Да, параметр «лямбда» получился просто сказочным, а кому сейчас легко?

Понеслась нелёгкая:

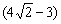
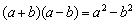
На последнем шаге я провёл умножение числителя и знаменателя на сопряжённое выражение – чтобы использовать формулу и избавиться от иррациональности в знаменателе.

Разбираемся со второй координатой:

Таким образом:

Предчувствие вас не обмануло, уравнение биссектрисы составим по точкам :

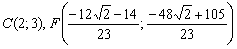
Проверил, всё сходится. На практике, конечно, вычисления почти всегда будут проще. Никого не хотел запугать, так уж получилось =)

И, кроме того, один из читателей сайта предложил ещё один, более короткий путь:

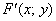
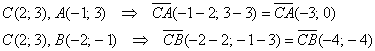
Способ второй. Рассмотрим произвольную точку биссектрисы, отличную от вершины и найдём векторы:

(именно такие! – не противоположные!), а также вектор .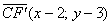

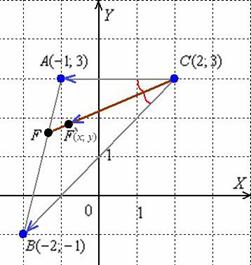
Запишем скалярное произведение: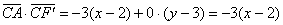
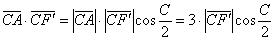
, но с другой стороны, по определению скалярного произведения:
Таким образом, получаем уравнение

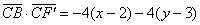
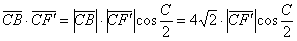
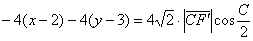
Запишем скалярное произведение . И с другой стороны: . Таким образом, получаем второе уравнение: .

В результате получается система двух уравнений: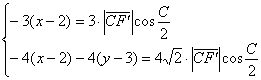

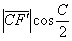
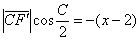
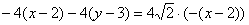
Произведения мы не знаем, но нам и не нужно его знать, из 1-го уравнения выражаем: – подставляем во 2-е уравнение:

и доводим его до ума: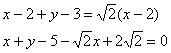

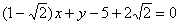
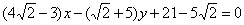
– искомое уравнение биссектрисы. И пусть вас не смущает, что предыдущим способом мы получили уравнение , у этих двух уравнений соответствующие коэффициенты пропорциональны (проверьте на калькуляторе), поэтому они задают одну и ту же прямую.

Если нужно найти точку пересечения биссектрисы с противоположной стороной, то никаких проблем:
– решите систему самостоятельно, и с помощью калькулятора убедитесь, что получились те же самые координаты, что и в предыдущем способе решения.

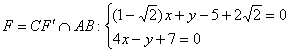
Но на этом всё не закончилось! Ещё один читатель предложил, пожалуй, самый простой вариант решения:

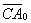
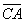
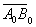
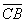
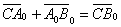
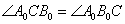
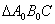
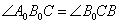
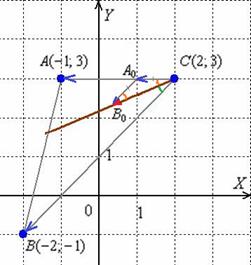
Способ третий: находим единичный вектор , коллинеарный вектору и единичный вектор , коллинеарный вектору . Их сумма – есть в точности направляющий вектор биссектрисы. Доказательство элементарно: – так как это углы при основании равнобедренного треугольника (оранжевые дуги на чертеже). И в свою очередь: – это накрест лежащие углы при параллельных прямых (проходили в школе). Таким образом, и вектор действительно является направляющим вектором биссектрисы:

Остальное – дело техники. Чтобы найти вектор единичной длины, коллинеарный данному, нужно координаты последнего разделить на его длину. По-научному нахождение соответствующего единичного вектора называется нормированием вектора: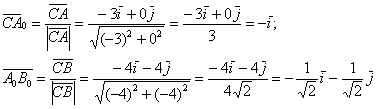

Самостоятельно убедитесь, что длины полученных векторов равны единице.

Найдём направляющий вектор биссектрисы:

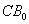
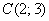
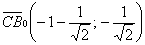
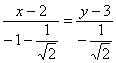
Уравнение биссектрисы составим по точке и направляющему вектору :

по правилу пропорции избавляемся от трёхэтажности: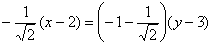

после чего избавляемся от дробей, умножив обе части на :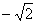

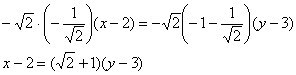
и окончательная причёска: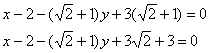

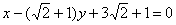
– искомое уравнение.

Коэффициенты полученного уравнения пропорциональны соответствующим коэффициентам уравнений, которые получены в двух предыдущих пунктах, и желающие могут убедиться в этом с помощью калькулятора.

Какой способ выбрать? По умолчанию, конечно, третий. Но лучше тот, который предложен в вашей методичке или на лекции. Так, первый, самый сложный способ как раз взят из конкретной методички.

Спасибо за ваши письма!

Как найти центр тяжести треугольника?

10) А что такое вообще центр тяжести плоской фигуры? Мысленно вырежьте из тонкого однородного картона любую фигуру. …Почему-то фигура зайца в голову пришла. Так вот: если слегка насадить данную фигуру центром тяжести (какой же я изверг =)) на вертикально расположенную иголку, то теоретически фигура не должна свалиться.

Центром тяжести треугольника является точка пересечения его медиан. В треугольнике три медианы и пересекаются они в одной точке. Из пункта № 7 нам уже известна одна из медиан: 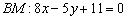. Как решить задачу? Можно найти уравнение второй медианы (любой из двух оставшихся) и точку пересечения этих медиан. Но есть путь короче! Нужно только знать полезное свойство:

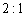
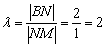
Точка пересечения медиан делит каждую из медиан в отношении , считая от вершины треугольника. Поэтому справедливо отношение

Нам известны точки .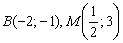
По формулам деления отрезка в данном отношении:

Таким образом, центр тяжести треугольника:

Заключительный пункт урока:

11) Составим систему линейных неравенств, определяющих треугольник.

Для понимания решения необходимо хорошо изучить статью Линейные неравенства. Системы линейных неравенств.

Для удобства перепишем найденные уравнения сторон:

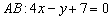
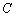
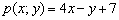
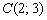
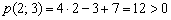
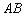
Рассмотрим прямую . Треугольник лежит в полуплоскости, где находится вершина . Составим вспомогательный многочлен и вычислим его значение в точке : . Поскольку сторона принадлежит треугольнику, то неравенство будет нестрогим:

Если не понятно, что к чему, пожалуйста, вернитесь к материалам про линейные неравенства.

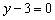
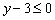
Рассмотрим прямую . Треугольник расположен ниже данной прямой, поэтому очевидно неравенство .

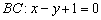
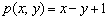
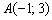
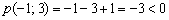
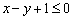
И, наконец, для прямой составим многочлен , в который подставим координаты точки : . Таким образом, получаем третье неравенство: .

Итак, треугольник 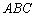определяется следующей системой линейных неравенств:

Как уже отмечалось, на практике рассмотренная задача с треугольником на плоскости очень популярна. Пунктов решения будет, конечно, не одиннадцать, а меньше, причём встретиться они могут в самых различных комбинациях. В этой связи вам придётся самостоятельно протягивать логическую цепочку решения. А вообще, всё довольно однообразно.

Может ещё задачку? Да ладно, не надо стесняться, я же по глазам вижу, что хотите =) Ненасытные читатели могут ознакомиться с решениями других задач по аналитической геометрии. Подходящий архив можно закачать на странице Готовые задачи по высшей математике.

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник