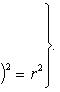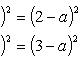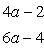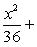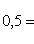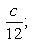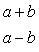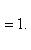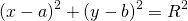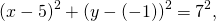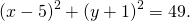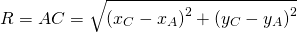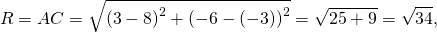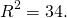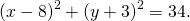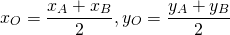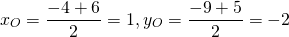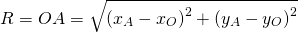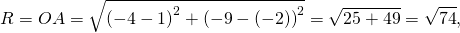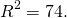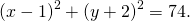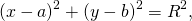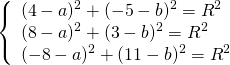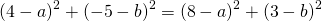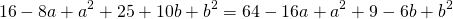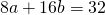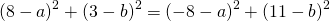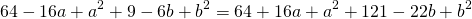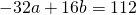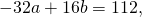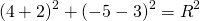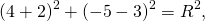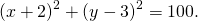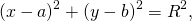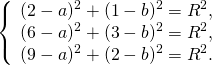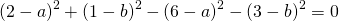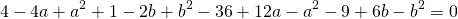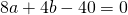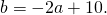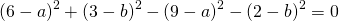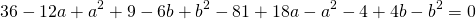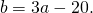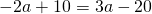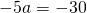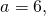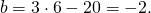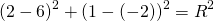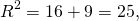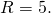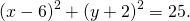Слово Как написать уравнение окружности проходящей через 3 точки - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Уравнение окружности, когда заданы три точки на окружности

Примеры:

Putting coordinates in eqn of circle, we get:
x1 2 + y1 2 + 2gx1 + 2fy1 + c = 0 – (1)
x2 2 + y2 2 + 2gx2 + 2fy2 + c = 0 – (2)
x3 2 + y3 2 + 2gx3 + 2fy3 + c = 0 – (3)

Now putting value of 2g from eqn (A) in (7) we get,
2f = ( ( x1 2 – x3 2 )( x1 – x2 ) +( y1 2 – y3 2 )( x1 – x2 ) + ( x2 2 – x1 2 )( x1 – x3 ) + ( y2 2 – y1 2 )( x1 – x3 ) ) / ( y3 – y1 )( x1 – x2 ) – ( y2 – y1 )( x1 – x3 )

Putting 2g and 2f in eqn (5) we get the value of c and know we had the equation of circle as x 2 + y 2 + 2gx + 2fy + c = 0

Ниже приведена реализация вышеуказанного подхода:

// C ++ реализация подхода
#include

using namespace std;

// Функция для поиска круга на
// в котором лежат данные три пункта

void findCircle( int x1, int y1, int x2, int y2, int x3, int y3)

// уравнение круга: x ^ 2 + y ^ 2 + 2 * g * x + 2 * f * y + c = 0

float r = sqrt (sqr_of_r);

findCircle(x1, y1, x2, y2, x3, y3);

// Java реализация подхода

// Функция для поиска круга на
// в котором лежат данные три пункта

static void findCircle( int x1, int y1,

// уравнение круга: x ^ 2 + y ^ 2 + 2 * g * x + 2 * f * y + c = 0

double r = Math.sqrt(sqr_of_r);

DecimalFormat df = new DecimalFormat( «#.#####» );

System.out.println( «Centre = (» + h + «,» + k + «)» );

System.out.println( «Radius = » + df.format(r));

public static void main (String[] args)

findCircle(x1, y1, x2, y2, x3, y3);

// Этот код предоставлен chandan_jnu

# Python3 реализация подхода

from math import sqrt

# Функция, чтобы найти круг на
# в котором лежат данные три балла

Источник

КРИВЫЕ ВТОРОГО ПОРЯДКА

— это уравнение определяет на плоскости окружность, эллипс, гиперболу и параболу.

Окружность.

— каноническое уравнение окружности

— уравнение окружности с центром в начале координат

— общее уравнение окружности

Для уравнения окружности выполнимо два условия:

1. коэффициенты при x и y равны между собой

2. отсутствует произведение текущих координат вида x*y.

Эллипс.

Эллипс – множество всех точек плоскости, сумма расстояний от каждой из которых до двух фокусов – величина постоянная и большая, чем расстояние между фокусами.

— каноническое уравнение эллипса

Основные понятия, связанные с уравнением эллипса:

1. Эллипс симметричен относительно координатных осей и относительно начала координат.

2. Точки пересечения с осью Ox , , а с осью Oy , .

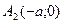
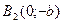
3. Точки — вершины эллипса.

4. Отрезки и , а также их длины 2a и 2b называются большой и малой осями эллипса. Числа a и b – большой и малой полуосями.

6. Если a>b, то эллипс вытянут вдоль оси Ox, а если a 0).

— каноническое уравнение параболы.

Основные понятия, связанные с уравнением параболы:

1. Поскольку в уравнении у в четной степени, парабола симметрична относительно оси Ox.

3. При x =0, y = 0 парабола проходит через начало координат.

4. Точка (0:0) называется вершиной параболы.

Отрезок FM называется фокальным радиусом точки М.

Уравнение тоже определяет параболу.

Решение:

Возьмем уравнения первое и второе, а потом первое и третье. Правые части этих уравнений между собой равны, значит, равны и левые их части, и мы получаем

Раскрывая скобки и упрощая, будем иметь

.

Подставляя эти значения a и b в первое из уравнений системы, получим

.

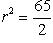
Искомое уравнение имеет вид

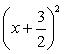
Задача 31. Составить простейшее уравнение эллипса, зная, что:
а) его полуоси a = 6, b = 4;
б) расстояние между фокусами 2c = 10, а большая полуось 2a = 16;
в) большая полуось a = 12, а эксцентриситет e = 0,5;
г) малая полуось b = 8, а эксцентриситет e = 0,6;
д) сумма полуосей a + b = 12, а расстояние между фокусами

Решение:

а) Простейшее уравнение эллипса имеет вид

.

Подставляя сюда a = 6, b = 4, получим

б) Имеем 2c = 10; c = 5; 2a = 16; a = 8.

в) a = 12; e = 0,5; известно, что ; в этой формуле неизвестно c. Для его определения получаем уравнение

.

Уравнение эллипса будет иметь вид

д) a + b = 12, .

Решая систему уравнений

получим, что a = 6,75, b = 5,25. Уравнение эллипса запишется в виде

Задача 32. Найти длины осей, координаты фокусов и эксцентриситет эллипса 4x 2 + 9y 2 = 144.

Решение:

Преобразуем это уравнение к простейшему виду

.

Разделив обе части заданного уравнения на 144, получим

.

Источник

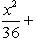
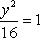
Написать уравнение окружности

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.

Следовательно, уравнение данной окружности

Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

Таким образом, уравнение окружности с диаметром AB —

Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение

получаем систему уравнений:

Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим

Приравняем правые части 2-го и 3-го уравнений:

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

Следовательно, уравнение окружности, проходящей через три данные точки —

Решение аналогично решению задания 4. В результате получим уравнение

Источник

Уравнение описанной окружности

Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?

Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.

Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).

Подставив координаты вершин треугольника в уравнение окружности

получим систему уравнений

Вычтем из первого уравнения системы второе:

Теперь из второго уравнения системы вычтем третье:

Приравняем правые части равенств b=-2a+10 и b=3a-20:

Подставим в первое уравнение системы a=6 и b=-2:

a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности

Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.

Источник

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

,

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Источник