Слово Как написать уравнение плоскости проходящей через точку перпендикулярно прямой - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.

В этой статье мы поговорим о том, как составляется уравнение плоскости, проходящей через заданную точку трехмерного пространства перпендикулярно к заданной прямой. Сначала разберем принцип нахождения уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой, после чего подробно разберем решения характерных примеров и задач.

Навигация по странице.

Нахождение уравнения плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой.

Поставим перед собой следующую задачу.

Сначала вспомним один важный факт.

Теперь покажем, как находится уравнение этой единственной плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.

Мы можем написать общее уравнение плоскости, если нам известны координаты точки, лежащей в этой плоскости, и координаты нормального вектора плоскости.

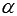
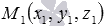
Итак, получаем алгоритм для нахождения уравнения плоскости , проходящей через заданную точку перпендикулярно к заданной прямой a :

Из найденного общего уравнения плоскости вида 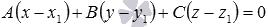можно, при необходимости, получить уравнение плоскости в отрезках и нормальное уравнение плоскости.

Примеры составления уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.

Рассмотрим решения нескольких примеров, в которых находится уравнение плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой.

Источник

Уравнение плоскости.

Общее уравнение плоскости

Любую плоскость можно задать уравнением плоскости первой степени вида

A x + B y + C z + D = 0

где A, B и C не могут быть одновременно равны нулю.

Уравнение плоскости в отрезках

x	+	y	+	z	= 1
a		b		c

Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали

Чтобы составить уравнение плоскости, зная координаты точки плоскости M( x ₀, y ₀, z ₀) и вектора нормали плоскости n = < A; B; C >можно использовать следующую формулу.

Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой

Если заданы координаты трех точек A( x ₁, y ₁, z ₁), B( x ₂, y ₂, z ₂) и C( x ₃, y ₃, z ₃), лежащих на плоскости, то уравнение плоскости можно найти по следующей формуле

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и перпендикуляной данной прямой. Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой − теория, примеры и решения

Построить уравнение плоскости α, проходящей через точку M₀ и перпендинулярной прямой L.

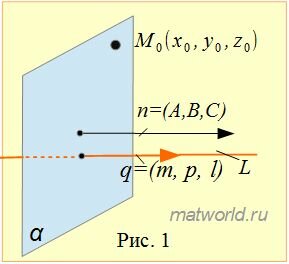Решение. Уравнение плоскости, проходящей через точку M₀ и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:

Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку прямая L и плоскость α перпендикулярны друг другу, следовательно нормальный вектор плоскостти и направляющий вектор прямой должны быть коллинеарны (Рис.1). Тогда вместо координат нормального вектора плоскости нужно подставить координаты направляющего вектора прямой L. Получим следующее уравнение плоскости:

Упростим уравнение (3):

Таким образом уравнение (4) определяет плоскость, проходящей через точку M₀(x₀, y₀, z₀) и перпендикулярной прямой (1).

Ответ. Уравнение плоскости прпоходящей через точку M₀(x₀, y₀, z₀) и перпендикулярной прямой (1) имеет вид (4).

Пример 1. Найти уравнение плоскости α, проходящую через точку M₀(3, −1, 2) и перпендикулярной прямой L:

Решение. Уравнение плоскости α, проходящей через точку M₀(x₀, y₀, z₀) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).

Направляющий вектор прямой L имеет следующий вид: :

Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (2) примет следующий вид:

Подставляя координаты точки M₀ и направляющего вектора q в (8), получим:

Упростим уравнение (9):

Ответ: Уравнение плоскости, проходящей через точку M₀(3, −1, 2) и перпендикулярной прямой (7) имеет вид (10).

Пример 2. Найти уравнение плоскости α, проходящую через точку M₀(4, 3, −6) и перпендикулярной прямой L, заданной параметрическим уравнением:

Решение. Приведем параметрическое уравнение (11) к каноническому виду:

Уравнение плоскости α, проходящей через точку M₀(x₀, y₀, z₀) и имеющий нормальный вектор n=<A, B, C> представляется формулой:

Направляющий вектор прямой L имеет следующий вид:

Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (12) примет следующий вид:

Подставляя координаты точки M₀ и направляющего вектора q в (13), получим:

Упростим уравнение (13):

Ответ. Уравнение плоскости, проходящей через точку M₀(4, 3, −6) и перпендикулярной прямой (11) имеет вид (14).

Источник

Уравнение плоскости, проходящей через прямую перпендикулярно заданной плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через прямую L₁ параллельно другой прямой L₂ (прямые L₁ и L₂ не параллельны). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямых (канонический или параметрический) введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Уравнение плоскости проходящей через прямую перпендикулярно заданной плоскости − теория, примеры и решения

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L

Пусть плоскость α₁ не перпендинулярно прямой L.

Задача заключается в построении уравнения плоскости α, проходящей через прямую L перпендикулярно плоскости α₁ (Рис.1).

Запишем уравнение искомой плоскости α:

Искомая плоскость α проходит через прямую L, следовательно она проходит через точку M₀(x₀, y₀, z₀). Тогда справедливо следующее равенство:

и поскольку прямая L принадлежит этой плоскости, то нормальный вектор n=<A, B, C> и направляющий вектор q=<m, p, l> ортогональны:

Для того, чтобы плоскость α была перпендикулярна плоскости α₁, нормальные векторы этих плоскостей должны быть ортогональными, т.е. скалярное произведение этих векторов должно быть равным нулю:

Таким образом мы должны решить систему трех уравнений с четыремя неизвестными (4)−(6). Представим систему линейных уравнений (4)−(6) в матричном виде:

Решив однородную систему линейных уравнений (7) найдем частное решение. (Как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн). Подставляя полученные коэффициенты A, B, C и D в уравнение (3), получим уравнение плоскости, проходящей через прямую L перпендикулярно плоскости α₁.

Пример 1. Найти уравнение плоскости α, проходящей через прямую L:

перпендикулярно плоскости α₁ :

Уравнение искомой плоскости α можно записать следующей формулой:

где n=<A, B, C> нормальный вектор плоскости.

а условие принадлежности прямой L к искомой плоскости α представляется следующим равенством:

Так как плоскость α должна быть перпендикулярна плоскости α₁, то должна выполнятся условие:

(13)

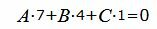(14)

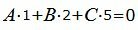(15)

Представим эти уравнения в матричном виде:

Решим систему линейных уравнений (16) отностительно A, B, C, D:

Таким образом искомая плоскость имеет нормальный вектор n=<A, B, C>=<9/43,−17/43,5/43>. Тогда подставляя в уравнение плоскости

значения A, B, C, D, получим:

Уравнение плоскости можно представить более упрощенном виде, умножив на число 43:

Ответ: Уравнение плоскости, проходящей через прямую (1) перпендикулярно плоскости (2) имеет вид (19).

Пример 2. Найти уравнение плоскости α, проходящей через прямую L:

перпендикулярно плоскости α₁ :

Уравнение искомой плоскости α можно записать следующей формулой:

где n=<A, B, C> нормальный вектор плоскости.

а условие принадлежности прямой L к искомой плоскости α представляется следующим равенством:

Так как плоскость α должна быть перпендикулярна плоскости α₁, то должна выполнятся условие:

(25)

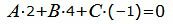(26)

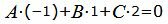(27)

Представим эти уравнения в матричном виде:

Решим систему линейных уравнений (28) отностительно A, B, C, D:

Таким образом искомая плоскость имеет нормальный вектор n=<A, B, C>=<3/2,−1/2,1>. Тогда подставляя в уравнение плоскости

значения A, B, C, D, получим:

Уравнение плоскости можно представить более упрощенном виде, умножив на число 43:

Ответ: Уравнение плоскости, проходящей через прямую (1) перпендикулярно плоскости (2) имеет вид (31).

Источник

Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой

Данная статья дает представление о том, как составить уравнение плоскости, проходящей через заданную точку трехмерного пространства перпендикулярно к заданной прямой. Разберем приведенный алгоритм на примере решения типовых задач.

Нахождение уравнения плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой

Через заданную точку трехмерного пространства проходит единственная плоскость, перпендикулярная к заданной прямой.

Теперь рассмотрим, как же найти уравнение этой единственной плоскости, проходящей через исходную точку и перпендикулярной данной прямой.

Возможно записать общее уравнение плоскости, если известны координаты точки, принадлежащей этой плоскости, а также координаты нормального вектора плоскости.

Определение координат направляющего вектора прямой a может осуществляться разными методами: зависит от варианта задания прямой a в исходных условиях. К примеру, если прямая a в условии задачи задана каноническими уравнениями вида

или параметрическими уравнениями вида:

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

Алгоритм для нахождения уравнения плоскости, проходящей через заданную точку перпендикулярно заданной прямой:

— определяем координаты нормального вектора плоскости α как координаты направляющего вектора прямой a :

Полученное общее уравнение плоскости: A ( x – x 1 ) + B ( y – y 1 ) + C ( z – z 1 ) = 0 дает возможность получить уравнение плоскости в отрезках или нормальное уравнение плоскости.

Решим несколько примеров, используя полученный выше алгоритм.

Решение

Рассмотрим еще один способ решить данную задачу:

Решение

Мы получили требуемое уравнение плоскости, проходящей через начало координат перпендикулярно к заданной прямой.

Решение

Общее уравнение плоскости будет записано в следующем виде:

Теперь составим искомое уравнение плоскости в отрезках:

Также нужно отметить, что встречаются задачи, требование которых – написать уравнение плоскости, проходящей через заданную точку и перпендикулярной к двум заданным плоскостям. В общем, решение этой задачи в том, чтобы составить уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой, т.к. две пересекающиеся плоскости задают прямую линию.

Решение

Тогда направляющим вектором α → прямой a возьмем векторное произведение векторов n 1 → и n 2 → :

Источник