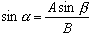Функция Excel SIN
Функция Excel SIN (Содержание)
Функция SIN в Excel
Способность вычислять не охватывает всю математику. Это подраздел, хотя и жизненно важный в его применении. В прошедшие годы это было ограничивающим фактором, за исключением очень известных и чрезвычайно талантливых «человеческих калькуляторов», таких как Шакунтала Деви. Но компьютеры теперь позволяют сделать всю математику более интеллектуальной. Понятия и теоремы математики сейчас важнее, чем когда-либо прежде.
Excel очень искусен в обработке множества математических моделей, вооружен обширным набором математических и логических функций для поддержки различных операций. Он предоставляет целый набор тригонометрических функций, которые помогают нам, когда мы вступаем в мир тригонометрии.
Наоборот, утилита DEGREES одинаково важна. Эта функция может использоваться для полной противоположности функции RADIANS путем преобразования радиан в градусы. Как пример, DEGREES (PI () / 2) оценивает 90.
Как использовать функцию SIN в Excel?
Давайте разберемся, как использовать функцию SIN в Excel, используя несколько примеров и реальных иллюстраций функции SIN в Excel.
Расчет значения синуса с использованием функции SIN в Excel
Чтобы найти синус определенного числа, мы должны сначала написать = SIN () в конкретной ячейке.
Как видно из приведенного выше снимка экрана, функция SIN в Excel ожидает ввод числа. Это число обычно представляет значение в радианах.
Как только мы сделаем это, мы получим значение SIN 60 градусов.
Расчет значения синуса с использованием функции SIN и RADIAN в Excel
Теперь давайте посмотрим, как мы можем использовать SIN более продуктивно, в случае, когда мы не знаем точное значение радиана для градуса.
Мы будем использовать RADIANS (), чтобы узнать значение радиана, которое мы передадим в качестве аргумента функции SIN.
Итак, начнем с более ранней версии SIN ():
Как видно из приведенного выше примера, RADIANS () принимает значение в градусах. Итак, мы передадим 60 как значение для RADIANS ().
Затем нажмите Enter. Это дает следующий результат.
Итак, мы видим, что результат такой же, как в первом примере.
Расчет значения синуса с использованием SIN и функции PI в Excel
Существует еще один способ преобразования значения градуса в радианы для использования в функции SIN. Из школьного времени мы помним, что π = 180 °. Итак, если угол в градусах, умножьте его на π / 180 °, чтобы преобразовать его в радианы. В Excel это преобразование может быть записано как PI () / 180. Например, чтобы преобразовать 60 ° в радианы, выражение для Excel будет равно 60 * PI () / 180, что равно 1, 0472 радиан.
Давайте посмотрим, как это работает:
Мы начнем с написания функции SIN так же, как описано выше.
Далее мы напрямую передадим 60 ° в качестве аргумента функции SIN. Но это не даст нам соответствующее значение 60 градусов в радианах. Следовательно, мы умножим 60 на PI () / 180.
Это даст нам следующий результат:
Как мы видим, это то же самое, что и приведенные выше примеры.
Теперь давайте посмотрим на другой пример, показывающий результаты функции SIN для различных значений.
Пояснения к результатам приведены в приведенной выше таблице:
Случай 1 и 2:
Случай 3 и 4:
Радианы и Pi / 180 имеют одинаковое значение в математике, и, следовательно, функция SIN дает одинаковое значение. В обоих примерах SIN равен 30 градусам, что дает значение 0, 5.
Случай 5 и 6:
Скажем, например, мы хотим знать высоту дерева на рисунке выше. Мы знаем, что если мы стоим в 76 м от вершины дерева (x = 76 м), то линия визирования к вершине дерева составляет 32 ° по отношению к горизонту (θ = 32 °). Мы знаем это:
Следовательно, чтобы определить высоту дерева h, находим h = x SIN θ.
Функция SIN имеет только один аргумент, который является числом. Число требуется для расчета SIN этого. Следовательно, очень важно преобразовать градусы в радианы, прежде чем найти синус этого числа.
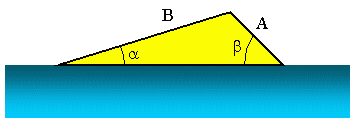
Теперь предположим, что мы хотим узнать угол запуска рампы для водных лыж, как показано на рисунке выше. Мы знаем, что A = 3, 5 м, B = 10, 2 м и b = 45, 0 °. Теперь, чтобы найти, мы можем использовать закон синусов. В этом сценарии это может быть записано как:
Мы можем реорганизовать это уравнение как:
Пример № 7
В нашем последнем тригонометрическом примере мы будем использовать Excel для проверки тригонометрической идентичности:
sin²θ + cos²θ = 1
Обратите внимание, что на скриншоте ниже эта идентичность сохраняется, когда θ задано в радианах и градусах.
Обратите внимание, что описание единицы измерения угла θ находится в разных ячейках, чем числа. Если мы поместим числа и единицы измерения в одну и ту же ячейку, Excel не сможет отличить число от текста, и поэтому мы не сможем ссылаться на ячейки для использования в уравнении, и это приведет к # ЗНАЧЕНИЮ! ошибка.
То, что нужно запомнить
Рекомендуемые статьи
Тригонометрические функции SIN COS в Excel для синуса и косинуса
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
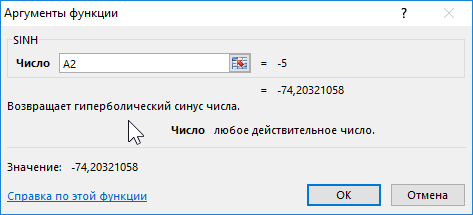
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
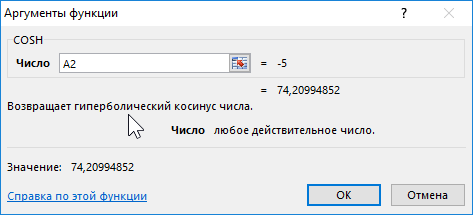
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
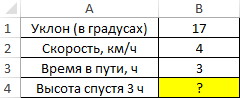
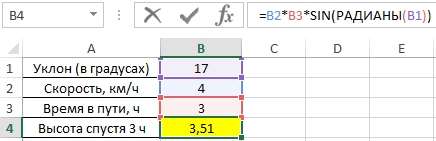
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Для решения используем формулу:
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
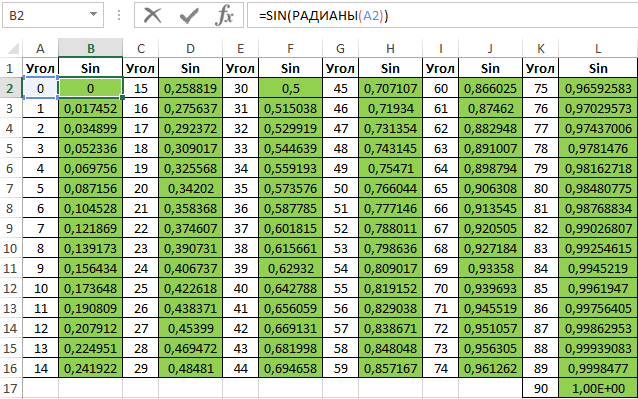
Таблица синусов и косинусов в Excel
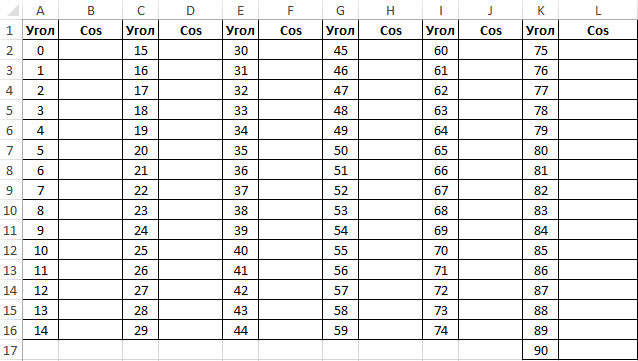
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
Вычислим значения для всех значений углов. Полученный результат:

Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
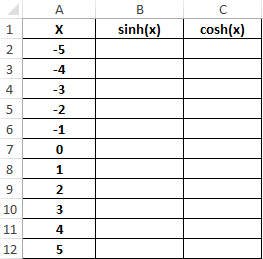
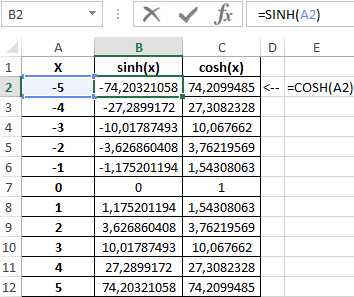
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Формула для нахождения синусов гиперболических:
Формула для нахождения косинусов гиперболических:
Таблица полученных значений:
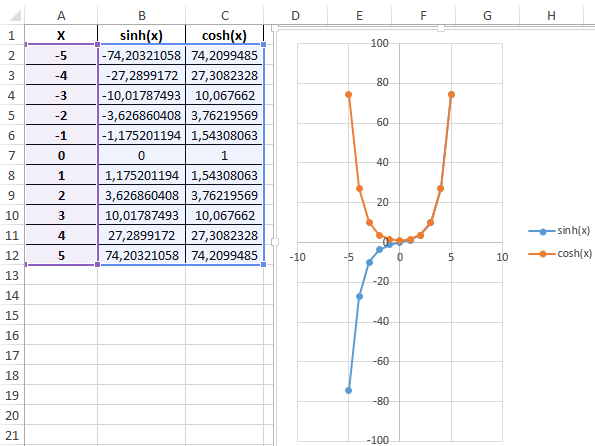
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
Синтаксис функции SINH:
Синтаксис функции COS:
Синтаксис функции COSH:
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
Функция SIN Excel
Функция SIN Excel — это встроенная тригонометрическая функция в Excel, которая используется для вычисления значения синуса заданного числа или, с точки зрения тригонометрии, значения синуса заданного угла, здесь угол — это число в Excel, и эта функция принимает только один аргумент. который является предоставленным входным номером.
Функция SIN в Excel
Функция SIN в Excel вычисляет синус указанного угла. Функция SIN в Excel классифицируется как функция Math / Trigonometry в Excel. SIN в excel всегда возвращает числовое значение.
В математике и тригонометрии SINE — это тригонометрическая функция угла, который представляет собой прямоугольный треугольник, равный длине противоположной стороны (прямоугольной стороны), деленной на длину гипотенузы и представленной как :
Sin Θ = противоположная сторона / гипотенуза
Формула SIN в Excel
Ниже представлена формула SIN в Excel.
Где число — это аргумент, передаваемый в формулу SIN в радианах.
Если мы напрямую передадим угол в SIN в функции excel, он не распознает его как допустимый аргумент. Например, если мы передадим 30 ° в качестве аргумента этому SIN в функцию Excel, она не распознает его как допустимый аргумент. Excel отобразит сообщение об ошибке.
Следовательно, аргумент, который нам нужно передать, должен быть в радианы.
Есть два метода преобразования угла в радианы.
Например, чтобы преобразовать 30 ° в радианы, мы воспользуемся этой функцией. Он принимает степень как число. Это будет 30 ° как 30.
знак равноРАДИАНЫ (30) даст радиан 0,52
Радиан = градусы * (π / 180) (π = 3,14)
В Excel также есть функция, которая возвращает значение Пи с точностью до 15 цифр, а функция ПИ()
Следовательно, для преобразования степени в радианы мы будем использовать формулу
Радиан = градусы * (PI () / 180)
Как использовать функцию SIN в Excel?
Функция SIN в Excel очень проста и удобна в использовании. Давайте разберемся в работе SIN in excel на нескольких примерах.
SIN в Excel, пример №1
Расчет значения синуса с использованием функции SIN в Excel и функции РАДИАНЫ в Excel
Расчет значения синуса с использованием функции SIN в Excel и функции PI
Функция синуса в Excel имеет множество реальных приложений; он широко используется в архитектуре для расчета высоты и длины геометрических фигур. Он также используется в GPS, оптике, вычислении траекторий, для поиска кратчайшего маршрута на основе географической широты и долготы, радиовещания и т. Д. Даже электромагнитная волна отображается в виде графика функции синуса и косинуса.
Предположим, у нас есть три прямоугольных треугольника с указанием их углов и длины одной стороны, и нам нужно вычислить длину двух других сторон.
Сумма всех углов треугольника равна 180 °; следовательно, мы можем легко вычислить третий угол.
Мы знаем, Sin Θ = противоположное / гипотенуза
Таким образом, длина противоположной стороны будет Sin Θ * гипотенуза
В Excel длина Противоположной стороны (перпендикулярной стороны) будет рассчитана по формуле SIN
= ГРЕХ (РАДИАНЫ (C2)) * E2
Применяя приведенную выше формулу SIN для трех треугольников, мы можем получить длину перпендикуляров треугольников
Для третьей стороны (смежной) у нас есть два метода — с помощью теоремы Пифагора или с помощью функции SIN в Excel с других углов.
Согласно теореме Пифагора, сумма квадратов двух сторон прямоугольного треугольника эквивалентна квадрату гипотенузы.
Гипотенуза 2 = Напротив 2 + Соседний 2
Соседний = (Гипотенуза 2 — Напротив 2 ) 1/2
В Excel мы запишем это как,
Применяя эту формулу, вычисляем длину смежной стороны
Используя второй метод, мы можем использовать SINE 3 rd угол для расчета значения прилегающей стороны
Если мы повернем треугольники на 90 ° влево, противоположная сторона поменяется местами со смежной стороной, и SIN угла между гипотенузой и смежной стороной поможет вычислить значение третьей стороны.
= ГРЕХ (РАДИАНЫ (D2)) * E2
SIN в Excel, пример №2
Есть высокое здание неизвестной высоты и солнечные лучи в точке, образующей угол в точке A 75 °, таким образом создавая тень от здания длиной 70 метров. Нам нужно найти высоту башни
Высота здания будет рассчитана с использованием SIN в функции excel.
SIN 75 ° = высота здания / длина тени в точке A
Следовательно, высота здания = SIN 75 ° * Длина тени в точке A
Следовательно, высота здания будет
= SIN (РАДИАНЫ (B3)) * B2
Высота здания 67,61 метра.
SIN в Excel, пример №3
У нас есть земля в форме треугольника, для которого заданы два угла 30 ° и 70 °, и нам известна только длина одной стороны треугольника, которая составляет 40 метров. Нам нужно найти длину трех других сторон и периметр треугольника.
Для треугольника, когда одна сторона и все углы известны, мы можем вычислить другие стороны по правилу SINE
Правило синуса в тригонометрии дает соотношение углов и сторон треугольника по формуле SIN
a / sin α = b / sin ß = c / sin δ
α = 30 °, ß = 70 ° и δ = 180 ° — (30 ° + 70 °) = 80 ° и одна сторона треугольника b = 40 метров
Чтобы найти другие стороны треугольника, мы воспользуемся правилом SINE
а = Sin α * (b / sin ß)
a = ГРЕХ (РАДИАНЫ (30)) * (B5 / ГРЕХ (РАДИАНЫ (70)))
Длина стороны а = 21,28 метра
Точно так же третья сторона c будет
c = Sin δ * (b / sin ß)
c = SIN (РАДИАНЫ (80)) * (B5 / SIN (РАДИАНЫ (70)))
Три стороны треугольника имеют длину 21,28, 40, 41,92 метра.
Периметр треугольника — это сумма всех сторон.
Следовательно, периметр будет = СУММ (B5: B7)
Как в экселе считать синус в градусах
В этой статье описаны синтаксис формулы и использование функции SIN в Microsoft Excel.
Описание
Возвращает синус заданного угла.
Синтаксис
Аргументы функции SIN описаны ниже.
Число Обязательный. Угол в радианах, для которого вычисляется синус.
Замечание
Если аргумент задан в градусах, умножьте его на ПИ()/180 или преобразуйте в радианы с помощью функции РАДИАНЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Для решения используем формулу:
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
Вычислим значения для всех значений углов. Полученный результат:

Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Формула для нахождения синусов гиперболических:
Формула для нахождения косинусов гиперболических:
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
Синтаксис функции SINH:
Синтаксис функции COS:
Синтаксис функции COSH:
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
В этой практической задаче я покажу вам как при помощи возможностей Excel 2010 найти значение косинуса угла в 136 градусов. Задачка из школьной программы, так что этот практический урок будет полезен не только родителям, но и школьникам. Заодно вы узнаете какими тригонометрическими функциями обладает Excel 2010.
Обратите внимание на то, что в тригонометрических функциях программы Excel углы измеряются не в градусах, а в радианах. Поэтому, прежде чем вычислить косинус угла 136°, его нужно перевести в радианы. Это можно сделать двумя способами.
Первый: умножить 136 на число пи и разделить произведение на 180.
Второй: воспользоваться специальной функцией, которая переводит градусы в радианы.
Как видите, на рис. 10.2 результат в обоих случаях одинаков.
Рис. 10.2. Вычисление косинуса: формулы (а) и результат (б)
Рассмотрим некоторые математические функции программы.